图形轮廓排序及顶点凹凸性判别的研究与实现

赵玉刚，张 健，于光伟，李海洋

（山东理工大学 机械工程学院，淄博 255049）

0 引言

在CAD/CAM系统中，尤其是在基于图形交互式的自动编程系统中，图形轮廓的排序及顶点凹凸性的快速自动识别是解决许多实际问题的基础，也是计算机图形学中一个基本的内容。图形轮廓的走向及其顶点凹凸性识别具有重要的使用价值，如在刀具轨迹路径的生成、多边形的三角剖析、轮廓特征点的基元关系判定、科学计算可视化和石材异型板上挖孔等方面均有应用。在模型识别、图像处理、曲面插值等方面常常遇到对多边形区域或离散点进行分割的问题，如能预先确定图形轮廓各个顶点的凹凸性，就可使问题的解决得到简化。

1 图形轮廓的排序

在图形交互式的数控自动编程系统CAD模块中，按时间先后顺序绘制的图形轮廓不一定首尾顺序连接，因此由绘图系统提供的图形元素在空间上是各自独立的，而在数控加工中，要求各个图元在空间上是连续的，即各个加工段之间是按顺序首尾相连的，因此要对这些在空间域上杂乱无章的图形元素按数控加工刀具轨迹所要求的顺序进行重新编排。

实现图形轮廓的排序，其核心思想是端点跟踪法。首先以选中的第一段图形元素的终点为依据点，在其它图形元素中寻找与这一点重合的端点。如果存在，则作为第二段图形元素，且将这个端点作为第二段图形元素的起点。如果不存在，则将第一段图形元素的起点与终点互换，然后再重复上面的过程，直到找到第二段图形元素。然后再以第二段图形元素的终点作为依据点，继续寻找下一段图形元素。将各图形元素按顺序依次排序，形成一个首尾顺序连接的封闭环。

图1既是图形轮廓排序的算法流程图，其中一些参数的意义如下：N为图形轮廓的边数，Pi,1、Pi,2表示第i条边的起点与终点坐标。

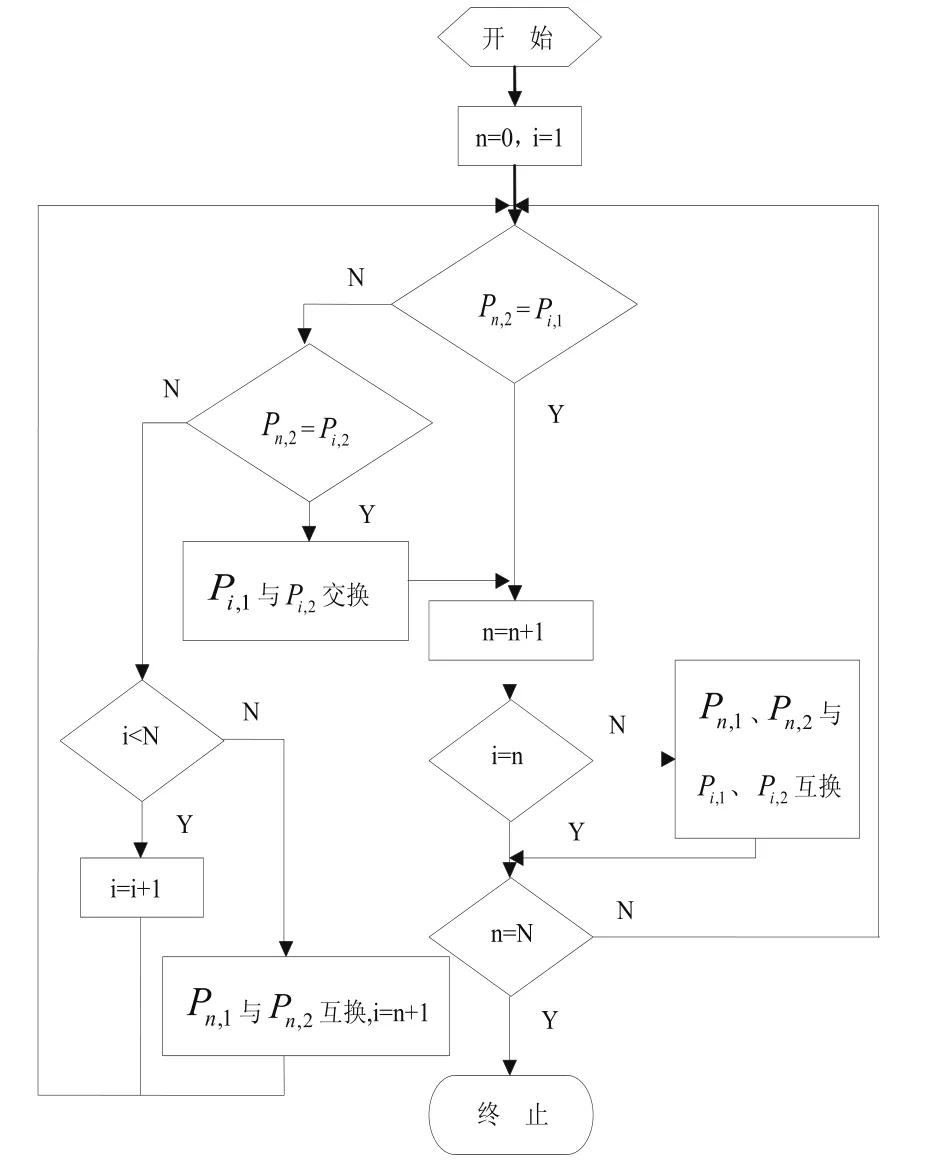
图1 图形轮廓端点排序流程图

从图形轮廓排序的算法流程图可以得到，以选择的第一段图形元素为起始边，各边按顺序连接组成封闭环。而这个封闭环也具有了一定的走向，再通过下面的最值法来确定图形轮廓的走向。

2 图形轮廓走向的判定

通过上面图形轮廓的排序，即可以得到一个图形轮廓串联环，而这个环是由一串坐标组成。我们找到图形轮廓所有顶点中的最高点，最高点的前一段图元和后一段图元构成的两个向量（即最高点连接的两条边的边矢向量）做叉乘，根据叉乘符号判别多边形是顺时针还是逆时针，符合右手法则。

判断图形轮廓顶点的最高点，其算法流程如图2。Pi,y代表第i条边终点的纵坐标值，N为图形轮廓的边数，j代表最高顶点所在的边。

图2 求解最高点的算法流程图

平面图形轮廓的特征点是指在多边形的所有顶点中，Y坐标值最大的那个顶点，即某图形轮廓最上面的那个顶点。最高顶点终点所在的边为j，这个顶点即为特征点。分两种情况讨论图形轮廓的走向：第一种情况，，不妨设为第j条边的向量，由起点指向终点，考察特征点处两条相邻边矢的叉积，记：；第二种情况，j=N，即最高点为最后封闭环的终点，而考察特征点处两条相邻边矢的叉积，记：。由的符号可知：符号为正时，图形轮廓的走向为逆时针（即四指的旋向为逆时针），如图3所示；反之，图形轮廓的走向为顺时针（四指的旋向为顺时针），如图4所示。

图3 逆时针走向

图4 顺时针走向

用特征点法能够快速确定平面图形轮廓的发矢方向，并由此初步判别出图形轮廓的走向。对于有圆弧存在的轮廓图形环，由圆弧的走向决定，通过最大Y坐标做垂直线，遍历所有的圆弧图元，搜索是否有圆弧图元与这条垂直线相交（交点Y坐标必须大于最大Y坐标），如果存在，记录圆弧图元的数目。如果存在的圆弧图元的数目为奇数时，则图形轮廓环的方向反向；如果存在的圆弧图元的数目为偶数时，则图形轮廓环的方向不发生改变。

3 图形轮廓顶点凹凸性自动识别

通过端点跟踪法对图形轮廓进行排序及最值法判断图形轮廓的走向，便可识别出多边形顶点的凹凸性。按边的顺序作矢量(j=1…N)，将沿图形轮廓的走向旋转到矢量方向，根据转过的角度来判断图形轮廓的顶点的凹凸性。如果转过的角度大于π，则图形轮廓的此顶点为凹顶点；如果转过的角度小于π，则多边形的此顶点为凸顶点。

4 图形轮廓排序及顶点凹凸性算法的实现

我们在计算机上用C++Builder，实现了图形轮廓的排序、走向及顶点凹凸性的判断，实验结果表明：此算法稳定可靠、实现简单、速度快。

图5 CAD模块绘制的多边形顶点数据

图6 排序后的多边形顶点数据

图5是在CAD/CAM自动编程系统的CAD模块中，随意绘制的多边形各边的端点数据，并以文本文档的格式保存。经过多边形的排序，得到如图6所示的多边形顶点数据。通过图6可以清晰的看到，将杂乱的数据整理成首尾顺序连接的有向封闭多边形。

图7 多边形的绘制

图7为在CAD/CAM自动编程系统中，利用CAD模块，初步建立的示范图形。其中所标注的数字所在的顶点是绘制的多边形各边的终点位置与前面的图5相对应，其中数据的顺序也代表了绘制多边形各边的先后顺序。假设在选择多边形各边加工时，选择的顺序同样按照图形标注的顺序选择。当然也可以随意的选择多边形各边。经过多边形的排序、走向的确定及凹凸性的判别。最终得到的如图8所示。

在图8中，经过图形轮廓的排序、走向的确定及顶点凹凸性的判别，其结果显示在统计窗口中，图形轮廓包括了7条边，在选择多边形加工时，选择的顺序为顺时针，得到两个凹顶点，分别用实心小圆标志。

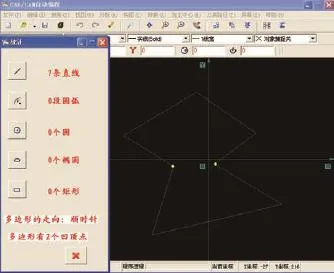
图8 多边形的排序及凹凸点判断

5 结束语

本文主要针对图形轮廓的排序、走向的确定及顶点凹凸性的判别，进行了分析和研究。在C++Builder环境下，验证算法的可行性，并实现了图形轮廓顶点凸凹性的判别。该方法使用于各种平面图形轮廓凹凸性的判别。而且在CAD/CAM自动编程系统中，具有很高的使用价值。

[1] 周培德.确定任意多边形凸凹性顶点的算法[J].软件学报,1995,6(5):276-279.

[2] 史万田.多边形顶点为凸凹点的计算机识别方法[J].计算机辅助设计与图形学学报,1990,2(3):15-16,23.

[3] 万书亭,韩庆瑶.平面多边形凸凹性的顶角判别法[J].水利电力机械,2003,(4):6-8.

[4] 汪学明.多边形顶点凸凹性识别算法的研究与实现[J].计算机应用,2005,(8):1786-1788.

[5] 刘晓平.简单多边形方向及顶点凹凸性的快速判断[J].工程图学学报,2005,(4):124-128.