推测变分及其在产业组织领域的应用
2010-07-09吴汉洪邱中虎
吴汉洪,邱中虎
(中国人民大学 经济学院,北京 100872)
推测变分这一思想最早产生于20世纪20年代,当时西方经济学正经历着不完全竞争理论的大发展。作为研究行为人之间相互作用的工具之一,推测变分有着完整的理论体系。即使在20世纪八九十年代产业组织理论体系经由博弈论进行演绎时,推测变分也是新经验产业组织的理论基础和计量工具,而且推测变分在动态相互作用研究中有着比博弈论更为广泛的应用。但国内对推测变分的研究尚处于空白状态,本文拟简要介绍推测变分这一理论体系以及其在新经验产业组织中的应用。
一、推测变分发展历程
推测变分(conjectural variation,以下简称CV)是指在与对手竞争时,厂商关于自己决策变量的变动会引起竞争对手决策变量反应程度的推测。这一思想首先出现在Bowley(1924)的著作中①,然后由Frisch(1933)正式的表述出来②。鉴于在两位先驱者所处的年代,数学表达形式尚未统一,在后人的研究中,一般采用另外一种标准的表述方法,如在Perry(1982)的文章中,其以同质产品产量竞争模型为基准,将推测变分表述为:
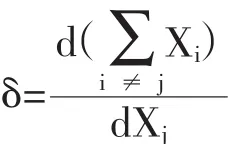
其中Xi表示厂商i的产量,而δ表述的是厂商j关于自己产量变化会引起其他竞争对手产量调整幅度的推测。在这里δ的取值范围为[-1,m-1],当δ=1时,市场竞争形式为完全竞争的,厂商j增加1单位产量会使得其他厂商总计1单位产量的缩减;而当δ=0时,市场竞争形式为古诺竞争,也即是说,厂商认为,自己产量的增减不会引起其他厂商产量的变化;当δ=m-1时,市场竞争形式为完全合谋形式,也即是说,厂商的产量变化会引起所有其他厂商同样的产量变化。这样,推测变分通过不同的取值覆盖了从完全竞争到完全合谋这一相当大的范围。
推测变分的出现,给出了古诺(1838)难题的一种解决方法。在古诺(1838)的著作中,使用了一个双寡头模型,模型中两个厂商在确定自己产量时都假定其他厂商的产量不变,从而在进行一系列调整之后市场达到均衡。从Bowley(1924)以及庇古(1924)的《福利经济学》起,人们开始认识到古诺形式的双寡头反应函数需要进行一个推测上的解释。问题的关键在于调和反应函数与古诺模型的静态设置,前者往往被看成动态概念,而后者混淆了只进行一次的同时博弈的静态构建与序贯博弈的动态描述,在古诺模型中,每个厂商不断地进行着行动、反应以及相应反应,序贯博弈能够更好地进行描述。特别的,古诺的反应函数被构造成一个静态概念,而每个厂商关于其他厂商实际产量的信息只能在序贯博弈中才能出现。古诺模型最受人诟病的是其对厂商行为的假设——每个厂商在行动时认定竞争对手不会对自己行动做出反应,但在古诺的拟动态描述中,每个厂商不可避免地会认识到其竞争对手绝不会是消极的而是会对自己行动做出反应的。这种假设以及静态动态之间复杂关系给人们造成了极大困难,Bowley和庇古都通过强调反应函数的推测性质来试图解决这些苦难:前者是通过引入推测变分而对古诺的假设进行推广,后者则是强调在任何寡头设置中心理特征的作用。但是如上面所说,这两扇对心理变量敞开的大门有一个主要的缺陷——双寡头均衡的不确定性,因为其使得介于完全竞争和垄断之间的所有市场结果都成为可能③。
推测变分的引入可以看作是一把双刃剑:一方面,证实了古诺模型结果的不确定性④,其实际上为庇古的观点进行数学形式的表达,庇古认为,每个厂商关于竞争对手的行为的推测可以是任意的,因此双寡头均衡注定是不确定的;另一方面,其也可被看做是呼吁对厂商推测赋予一特定值,从而在所考察的特定案例中这些均衡结果无疑是具有确定性的,而这种事先的不确定性也为经验研究提供了便利,可以利用经验研究确定推测变分的某一个特定值,而该特定值是与某个市场竞争程度相对应的,这就为市场竞争程度的经验研究提供了理论指导和经验工具。
但是推测变分也不是没有缺陷的,首先,由于厂商所推测的竞争对手反应与实际发生的情况并不一致,即使市场出现均衡,也会出现如Fellner(1949)所说的厂商“误打正撞”的现象⑤。其次,由于推测变分通过引入心理变量使得其能够覆盖相当大一部分范围的市场竞争情况,这就牺牲了其预测能力,按照波普尔的可证伪性判断标准或者弗里德曼的实证经济学准则,这就使得人们对推测变分的满意程度很低。最后,由于推测变分通过引入心理变量将古诺的动态调整过程处理作一种发生在行为人内心的心理实验,并直接面对的是市场均衡的结果,从而对市场趋于均衡的过程难于进行解释。所有这三方面,使得许多新古典经济学家不愿意使用推测变分这种工具⑥。
由于推测变分均衡的不确定性,以及推测变分与竞争对手实际反应在本质上的不一定吻合,这就使得人们开始探讨如何对推测变分均衡施加一定的限制条件(一致性条件或被称作理性条件),以使推测变分均衡是具有一致性的或者是理性的。所谓一致性推测变分,是指参与者关于自己变量变动所导致竞争对手反应的推测与竞争对手实际反应是相同的,可以表述为⑦:


引入一致性推测变分概念使得推测变分均衡的范围大为缩小,但是,其本质——将原本为动态过程的市场调整过程处理成静态概念——仍然没有变化,对此,推测变分拥护者认为推测变分是动态相互作用的静态结果。在博弈论中,无名氏定理认为在无限期的重复博弈下,从古诺均衡到完全合谋的所有均衡结果都可能发生,这种均衡结果与某一给定推测变分值的静态均衡结果是相同的。Cabral(1995)认为,在线性寡头中,这种对应关系实际上是在T期最小最大惩罚策略下产量设定重复博弈下成立的;而在Dockner(1992)考虑动态寡头竞争与静态推测变分均衡之间的关系,发现稳态开环均衡与静态古诺解相吻合,但稳态完美均衡与之并不吻合。动态博弈的稳态完美均衡可以看做是相对应静态博弈的推测变分均衡,因此,在极端情况下,静态推测变分分析近似于长期动态相互作用。因而,我们的发现可以为静态推测变分分析用于模型化动态相互作用提供一些辩护。
至此,推测变分本身的理论体系已经完成。纵观推测变分理论的发展历程,可以发现,推测变分通过引入心理因素将古诺的动态调整过程处理成一种心理实验,从而解决了古诺均衡的存在性问题,然后通过一致性条件的限制使得推测变分与其他厂商实际反应相一致从而确保推测变分均衡的理性基础。
在发展一致性推测变分的同时,人们也关注其他决策变量的推测变分,如价格推测变分、广告推测变分、研发推测变分等,基本囊括了产业组织领域厂商的所有决策变量。作为与产量推测变分相对应的价格推测变分,引起了人们的广泛关注。Mul-ligan and Fik(1989)讨论了空间竞争模型中不对称价格推测变分的情况,而Kamien and Schwartz(1983)在差异化产品对称均衡中证明了在市场结果(价格和产量)意义上等价的价格推测变分和产量推测变分之间的关系:
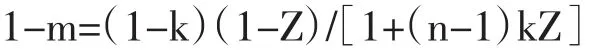
其中Z=P2/P1,0<Z<1,m为价格推测变分,k为相应的产量推测变分。在他们的简单模型中,这一关系在参数上依赖于竞争对手的数目和对产品差异程度的认识。在极限情形下,如果k=1,那么m=1。如果厂商预期产出上的调整会被完全模仿,那么这就隐含的意味着其价格调整会也被完全的模仿,反之亦然。在另一极端,如果k=-1/(n-1),那么m=-1/(n-1)。如果每个厂商都相信其产量的增加会刚好被其他竞争对手产量减少所抵消从而行业产量不变,那么其也就潜在的假设其价格的增加会被其每个竞争对手价格减少所抵消,从而行业销售量保持不变。
二、推测变分的特点:与博弈论相比较
推测变分方法和博弈论方法同属于研究行为人之间相互作用的方法。1924年,Bowley的著作宣告了推测变分理论的正式诞生;1928年,冯·诺依曼证明了博弈论的基本原理,宣告了博弈论的正式诞生。1944年,冯·诺依曼和摩根斯坦的《博弈论与经济行为》将二人博弈推广至多人博弈情形并将博弈论系统的应用于经济领域,奠定了这一学科的基础和理论体系。
在对古诺(1838)提出的经济稳定性难题的解决中,推测变分方法是通过引入心理变量将古诺的动态调整过程转变为静态情形,也即是将在现实中发生的不断试错的过程转换为行为心理实验的过程,这种方法被后人称作心理方法;而另一种方法则是考察对需求和成本函数需要施加什么样的限制,才能使经济在古诺的动态调整过程下趋于稳定,这种方法则被称作机制方法。那么就推测变分与博弈论相比较而言,他们之间的根本差别就在于对这两种思路的继承。推测变分先通过引入心理变量考察均衡,然后要求行为人推测与实际相一致来实现均衡的一致性;而博弈论则是通过对行为人策略集、信息集以及支付函数的详细规定,通过行为人之间的相互作用(这里的相互作用并不一定如古诺(1838)那样为实际的动态调整过程,也可以是存在于行为人头脑中的实验过程,这在静态博弈中尤其如此),使得经济趋于均衡,在均衡概念本身中就存在着一致性。这种根本差别导致了推测变分方法与博弈论方法之间存在着以下一些差别:
1.推测变分均衡本身并不存在一致性,因此需要通过要求行为人的推测与竞争对手的实际反应相一致来实现均衡的一致性,而博弈论均衡概念本身就蕴含着一致性要求,行为人在均衡处都不愿意改变自己的行为。
2.推测变分对行为人的信息集和策略集并没有严格的要求,而博弈论则需要详细规定行为人的信息集和策略集。
3.推测变分对行为人的行动次序并没有严格的要求,而博弈论则需要严格规定行为的行动次序,因为推测变分是直接考察市场均衡,而博弈论则是主要着眼于行为人的相互作用过程。行动次序对行为人的信息集有着显著的影响从而在博弈论中占据着重要的地方。
以上3个差别使得推测变分在处理动态相互作用、有限信息和有限理性问题上相对于博弈论有着更大的便利。
三、推测变分在理论研究中的作用
1.推测变分作为动态相互作用的简化形式。在前面我们看到,推测变分可以作为动态相互作用的简化形式,而这种简化可以为我们研究行为人之间的动态相互作用提供极大的便利,这一便利使得推测变分得到了广泛的应用,如Itaya and Shimomura(2001),Itaya and Okamura(2003)对公共品私人供给的研究;Dockner(1992),Driskill and McCafferty(1989),Cabral(1995) 对寡头的研究;Wildasin(1991),Figuieres(2002)对公共设施竞争的研究等。
2.动态设置下的一致推测变分。在Fershtmann and Kamien(1985)模型中,将推测变分与推测变分均衡引入微分博弈理论中,从而为微分博弈中开环均衡和闭环均衡提供了一个新的解释:开环纳什均衡为弱控制一致性推测均衡,而弱控制一致性推测均衡为闭环无记忆均衡。
Laitner(1980)模型为离散时间无限规划区间的两人重复博弈模型,同时考虑到跨期调整的成本,其发现该模型中推测变分均衡存在无限多个。
Friedman(1968)考虑了一离散时间无限规划区间的人博弈模型,Friedman先考虑了一有限规划区间的最优控制问题,然后将时间推向无穷,从而得到无限规划区间情形的结果。其总结了最优有限规划区间反馈控制趋向最优静态反馈控制的条件,也证明了反馈均衡弱形式的存在性。
3.动态推测变分、不完全信息与学习。至目前为止,对有限信息有限理性的处理还没有得到一个统一的框架,可能的框架有推测变分模型和进化模型。在推测变分方面,Itaya and Dasgupta(1995)、Friedman and Mezzetti (2002)、Jean-Marieand Tidball(2002)做出了突出贡献。
在Itaya and Dasgupta(2002)模型中,行为人的推测随着时间的推移而发生变动,在每一时点,行为人在给定对其他行为人的推测情况下选择一个最优反应。实际的最优反应可能与其推测的反应函数并不一致,行为人根据推测最优反应与实际最优反应之间的差异对自己的推测进行调整,所得出的调整过程类似“蛛网”模型而收敛于纳什均衡。
Friedman and Mezzetti(2002)提出了一折现重复博弈。在该模型中,在两个时间段之间,行为人推测竞争对手的反应是自身策略的变分。在给定这一推测下,存在一最优静态反馈策略,这一反馈规则可以得出一动态策略系统。在适当的条件下,采用的策略收敛至某一极限。在伯川德寡头情形中,这一极限对应于相应静态博弈的推测变分均衡,此时折现系数趋近于1,并且对于每一折现系数,静态策略对应着一个常数推测变分均衡,此处的推测变分可以通过一定方式求出。
在Friedman and Mezzetti(2002)的基础上,Jean-Marie and Tidball(2002)提出了一个离散时间学习模型,其中参与者关于其他参与者的推测是线性的。参与者一步一步的最优化其推测支付函数,并试图了解其竞争对手线性推测的斜率,这就得到了推测的动态调整过程。在支付函数、学习参数和参照点满足一定条件的情况下,在古诺和伯川德双寡头情形中,这一过程的稳态厂商策略趋向于卡特尔解。
另外,其他一些学者试图探讨静态博弈的推测变分均衡与进化博弈之间的关系。在Dixon and Somma(2003)和Müller and Normann(2002)文章中都使用了线性二次型模型,也即需求函数是线性的,厂商的成本是二次型的。厂商的成本函数为如下形式:
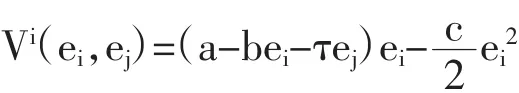
两者都认为通过直接计算,如果c>0,唯一的稳定进化策略就是其静态博弈的推测变分策略。当成本是线性时(c=0),Dixon and Somma(2003)认为尽管存在一致推测变分均衡,但是并不存在稳定进化策略,而此时一致推测变分均衡就是伯川德解。
四、推测变分在经验研究中的作用
在前面说到,推测变分由于其能够囊括从完全竞争到垄断所有的市场结构,这把双刃剑在使得其招致批评的同时,引起了经验研究学者的广泛注意。目前在对市场力量的经验研究中常用的方法有两种,一种是Non-nested模型,其方法是根据若干种特殊理论模型得出市场力量的若干个参数,然后用数据进行验证,然后选择最适合数据的模型,以此描述市场力量的实际情况;另一种就是行为参数模型,在这种方法中,使用行为参数,实际上仍然是推测变分,然后应用结构模型对该行为参数进行估计,得出推测变分的一个具体值,以此值表示市场力量的大小。在这里需要注意的是,此处所使用的行为参数与标准的推测变分有一定的差别,标准的推测变分中强调的是厂商关于自己变量变动对其他所有厂商影响的推测,而行为参数强调的是厂商产量变动对市场上每个厂商的平均变动情况的影响,有这样一个表达式:
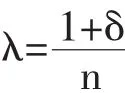

新经验产业组织的标志之一就是使用行为参数利用结构模型对市场力量进行估计。早在1974年,Iwata就提出通过推测变分来估计市场力量,用以克服在传统产业组织经验研究范式SCP中存在的缺陷⑧。Anderson(1977)认为在市场绩效与推测变分之间存在着简单的关系:当推测变分大于0时,厂商行为是模仿型的,也就是说厂商之间存在某种合谋;当推测变分等于0时,厂商行为是古诺型的;当推测变分小于0时,厂商行为是自适应的(adaptive behavior)。而Just and Chern(1980),Bresnahan(1982)和Lau(1982)提出使用行为参数以包罗所有市场结构,这标志着新经验产业组织的正式崛起。
在典型的结构性模型中,有两个基本方程:需求方程和边际成本方程。市场(或厂商)所面临的反需求函数为:
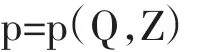
其中p为价格,Q为产量,Z为影响行业需求曲线但不影响边际成本的外生变量。边际成本曲线为
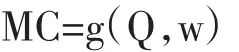
其中w为影响“行业”边际成本但不影响需求函数的外生变量。有效边际收入方程为
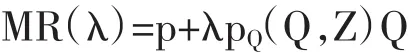
则最优条件或者均衡条件为行业的有效边际收入等于其边际成本:
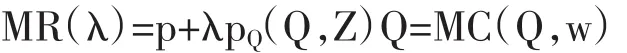
这样基本的模型由两个方程组成,一个是需求方程,另一个为最优条件方程。
如果市场是完全竞争型的,那么均衡由需求曲线(MR(0))和边际成本曲线的交点确定,如果市场为垄断的或者完全卡特尔化的,那么边际收入曲线就为MR(1)。而且可以在同质寡头模型下考虑λ的实际含义,在同质寡头古诺竞争模型中,λ等于厂商个数的倒数,也就是说,可以通过λ来大致判断市场上的竞争程度,如在美国纺织品市场上,Perloff and Ward(1988)测得的λ为0.21,这说明该市场上的竞争程度相当于5个同质寡头进行古诺竞争时的情形。
在新经验产业组织的研究过程中,对λ的解释主要有两种(Bresnahan,1989),对厂商所从事博弈持不可知论的学者将λ看作为对价格和边际成本之间差异的测量:p-MC=-λpQQ,而勒纳指数为:
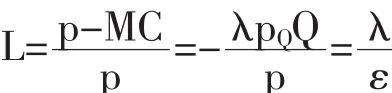
那么λ=-Lε,这种观点认为λ为经市场需求弹性调整过的勒纳指数。
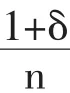
而对于λ为价格边际成本差异的解释,Corts(1999)认为,只有在潜在的厂商行为是推测变分均衡的结果时,所估计的推测变分参数才是无偏的。而且λ作为市场力量的指标,有着一个更为严重的问题,如果说厂商都提高价格缩减产量,那么所得λ为正,我们能够理解其存在合谋,但是如果厂商都降低价格进行产量扩张,那么所得λ仍然为正,这有可能是因为厂商之间进行价格竞争而不是一种合谋行为,也就是说根据λ对市场力量进行判断,还是具有一定的缺陷,需要我们结合其他数据具体分析。
五、结论
推测变分作为对古诺问题的一种解决方式,通过推测引入心理变量将古诺的动态调整过程处理成发生于行为人内心的心理实验,从而解决了经济的稳定性问题,但是,由于推测变分均衡本身并不存在一致性,需要对其施加理性条件或一致性条件。尽管一致性推测变分使得推测变分均衡的范围大为缩小,其本质仍未改变,对推测变分的更好解释可能是作为动态相互作用过程的静态表现形式。相对于博弈论,推测变分站在动态相互作用的结果层面,有利于其解决更为复杂的动态相互作用过程,因为博弈论在处理行为人的相互作用时强调相互作用的过程,这影响了其在处理更为复杂的相互作用问题中的作用,而利用推测变分处理动态相互作用,有利于处理过程的简化。在有限理性和有限信息问题的处理中,推测变分和进化博弈作为两种可能的发展方向,它们之间也存在着千丝万缕的联系。
推测变分对相互作用结果的专注也使得其在经验研究中的作用至关重要,新经验产业组织本身无论是从理论基础还是计量模型,都建立在推测变分基础之上,尽管仅仅依赖于这一简单工具受到人们的不少质疑,但是还没有出现一种更为合理的处理工具。
在实际商业经营管理中,推测变分也发挥着重要作用,作为考虑行为人相互作用的两种工具之一——博弈论,由于其纠缠于作用过程而且在经验检验中的能力不强,使得博弈论方法在实际经营管理中很少得到真正的应用,而另一种工具——推测变分,由于其专注于相互作用的结果并且可以由实践进行检验,这就使得其在实际经营管理中有着广大的空间,正如管理学杂志所倡导的那样,企业家应该将推测用于改进企业的计划过程和竞争地位⑨。
正是如此,Charles Figuieres et al(2003)认为推测变分在近期有着复兴的迹象。
注释
①在Bowley(1924)的著作中,其提出的数学表达式Dx2(x1),其表示的是厂商1产量x1关于厂商2产量x2的导数。Bowley认为均衡结果的求解依赖于每个生产者关于其他人可能会怎么做的设想,并提出在每个厂商的边际价格等于销售价格(Marginal price for each=selling price)所确定价格的邻域中可能存在一些振荡,见Bowley(1924)第38页。
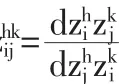
③更详细的论述,可以参见Nicola Giocoli(2003)。
④Jean Magnane Bornier J.1992。
⑤“Do Right for Wrong Reasons”,见Fellner(1949)。
⑥Nicola Giocoli(2005)。
⑦与上文相对应,仍然使用Perry所定义的一致性推测变分概念,见Matrin K.Perry(1982),数学程度更高的表述方法,可以参见Charles Figuieres,Alain Jean-Marie,Nicolas Tidball(2003)。另外一致性还可分为全局一致性和局部一致性:全局一致性是指推测变分在保持与实际反应相一致的同时并不随着时间变化而变化,而在整个时间范围内为常数;而局部一致性则是指在某个时点推测变分与实际反应相一致,但是随着时间的变化,推测变分的值可能会发生变化。
⑧见Iwata.Gyoichi.1974。另外,关于传统SCP范式存在的缺陷,可以参考Perloff,M.Jeffrey,Larry S.Karp and Amos Golan,2007.Estimating Market Power and Strategies,Cambridge University Press.
⑨Amit,Domowitz and Fershtman,1988,“Thinking one step ahead:the use of conjectures in competitor analysis”,Strategies Management Journal,Vol.9,pp.431-442。转引自J·卡布尔《产业经济学前沿问题》,中国税务出版社,2000年。
[1]Bowley,A.L. (1924),The Mathematical Groundwork of Economics,Oxford University Press,Oxford.
[2]Bresnahan Timothy F.(1982).“The Oligopoly Solution Concept Is Identified.”Economics Letters 10:87-92.
[3]Bresnahan,Timothy F. (1989).“Empirical Studies of Industries with Market Power.”In Richard Schmalensee and Robert D.Willig,eds.,The Handbook of Industrial Organization,pp.1011-1057(Amsterdam:North-Holland).
[4]Charles Figuieres, Alain Jean-Marie, Nicolas Querou and Mabel Tidball (2003)”The Theory of Conjectural Variations”,World Scientific.
[5]Corts,Kenneth S.(1999).“Conduct Parameters and the Measurement of Market Power”,Journal of Econometrics Vol.88,pp.227-250.
[6]Dixon,H.and Somma,E.(2003),“The Evolution of Consistent Conjectures”,Journal of Economic Behavior&Organization,Vol.51,pp.523-536.
[7]Driskill,R.A.and McCafferty,S. (1989),“Dynamic Duopolywith Adjustment Costs:aDifferentialGame Approach”,Journal of Economic Theory,Vol.49,pp.324-338.
[8]Engelbert J.Dockner (1992),“A dynamic theory of conjectural variations”,The Journal of Industrial Economics,Vol.40,No.4,pp.377-395.
[9]Fellner, W. 1949.Competition among the Few.New York:Knopf.
[10]Fershtman,C.and Kamien,M.I.(1985),“Conjectural Equilibrium and Strategies Spaces in Differential Games”,Opt.Control Theory and Economic Analysis,Vol.2,pp.569-579.
[11]Figuieres,C.(2002),“Complementarity,Substitutability and the Strategic Accumulation of Capital”,International Game Theory Review,Vol.4(4),pp.371-390.
[12]F.J.Anderson,(1977),“Market Performance and Conjectural Variations”, Southern Economic Journal, Vol.44,No.1,pp.173-178.
[13]Friedman,J.W. (1968),“Reaction Function and the Theory of Duopoly”,Review of Economic Studies,pp.257-272.
[14]Friedman, J.W.and Mezzetti, C.(2002),“Bounded Rationality,Dynamic Oligopoly,and Conjectural Variations”, Journal of Economic Behavior and Organization,Vol.49,pp.287-306.
[15]Frisch,R.,1933 “Monople,Polypole-La notion de force en Economie”,National konomisk Tidsskrift,Vol.71,pp.241-259(reprinted“Monopoly,polypoly:the concept of force in the economy”in International Economic Papers,Vol.1,pp.23-36,1951).
[16]Gordon F.Mulligan and Timothy J.Fik(1989),”Asymmetrical Price Conjectural Variation in Spatial Compe-tition Models”,Economic Geography,Vol.65,No.1(Jan.,1989),pp.19-32.
[17]Itaya,J.-I,and Dasgupta,D. (1995),“Dynamics,Consistent Conjectures,and Heterogeneous Agents in the Provision of Public Goods”,Public Finance,Vol.81,pp.371-389.
[18]Itaya,J.-I.and Okamura,M.(2003),“Conjectural Variations and Voluntary Public Good Provision in a Repeated Game Setting”,Journal of Public Economic Theory,Vol.5(1),pp.51-66.
[19]Itaya,J.-I.and Shimomura,K.(2001),“A Dynamic Conjectural Variations Model in the Private Provision of Public Goods:a Differential Game Approach”,Journal of Public Economics,Vol.81,pp.153-172.
[20]Iwata.Gyoichi.1974, ”MeasurementofConjectural Variations in Oligopoly.”Econometrica 42:947-966.
[21]【英】J·卡布尔.产业经济学前沿问题[M].北京:中国税务出版社,2000.
[22]Jean Magnane Bornier,J.1992,The“Cournot-Bertrand Debate”:A Historical Perspective,History of Political Economy,Vol.24,No.3 pp.623-656.
[23]Jean-Marie,A.and Tidball,M. (2002),“Adapting Behaviors through a Learning Process”,LAMETA Working Paper DT 2002-10,University of Montpellier 1.
[24]Just,Richard E.,and Wen S.Chern.1980.“Tomatoes,Technology,and Oligopsony.”Bell Journal of E-conomics and Management Science 11:584-602.
[25]Laitner,J. (1980),“Rational Duopoly Equilibria”,The Quarterly Journal of Economics,pp.641-662.
[26]Lau,Lawrence J.(1982),“On Identifying the Degree of Competitiveness from Industry Price and Output Data”,Economic Letters 10:93-99.
[27]Luis M.B.Cabral(1995),“Conjectural variations as a reduced form”,Economics Letters 49,397-402.
[28]Martin K.Perry 1982,“Oligopoly and Consistent Conjectural Variations”, The Bell Journal of Economics,Vol.13,No.1(Spring,1982),pp.197-205.
[29]Morton I.Kamien and Nancy L.Schwartz (1983),“Conjectural Variations”,The Canadian Journal of E-conomics Vol.16,No.2(May,1983),pp.191-211.
[30]Müller,W.and Normann,H.-T.(2002),“Conjectural Variations and Evolutionary Stability:a new Rationale for Consistency”,manuscript.
[31]Nicola Giocoli 2003,“’Conjecturizing’Cournot:The Conjectural Variations Approach to Duopoly Theory”,History of Political Economy 2003 35(2):175-204.
[32]Nicola Giocoli 2005,“The escape from conjectural variations:the consistency condition in duopoly theory from Bowley to Fellner”,Cambridge Journal of Economics 2005,29,601-618.
[33]Perloff,Jeffrey M.and Michael B.Ward.(1988),“A Flexible,Nonparametric Approach to Estimating Market Power”,Working Paper.
[34]Wildasin D.E.(1991),“SomeRudimentary‘Duopolity Theory’”,Regional Science and Urban Economics,Vol.21,pp.393-421.
