战役供应保障网络优化设计模型与算法＊

王文峰 董付强

（空军装备研究院雷达所1） 北京 100085） （中国人民解放军93856部队2） 兰州 730060）

现代战争作战物资消耗大，装备保障影响着战争的进程，甚至在一定程度上左右了战争的结局.因此，根据作战任务的实际需求，优化保障设施布局、完善军事物流网络，是战役装备保障的重要工作［1］.本文以防御作战条件下的战役弹药供应保障为背景，在对战役保障网络优化设计问题的特征进行分析的基础上，建立了优化决策模型，进而探讨模型的求解方法，最后用一个示例实验说明了模型的正确性.

1 战役装备保障网络优化设计问题特征分析

典型的战时装备保障物流系统的纵向结构如图1所示，作战装备和物资依靠战略、战役、战术保障力量，从后方基地经前沿基地、前进基地、补给站等各级保障设施，最终对作战部队实施保障.战役装备保障网络优化设计主要解决以下问题：根据特定战役阶段内作战部队的分布状况以及预计的物资保障需求，结合后方基地、前沿基地的布局状况，综合考虑战役保障中可用的战役、战术运输保障力量以及设施容量、保障时间约束等诸方面的限制，优化战役保障设施的选址、资源储备布局以及运送方案，为各作战部队提供最大可能的及时性保障.

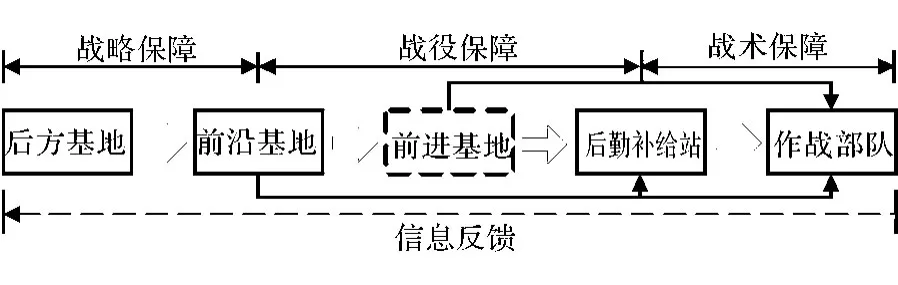
图1 装备保障物流系统结构

2 战役装备保障网络优化设计模型

本文将战役保障网络抽象为一个由基地和补给站2级设施以及需求点构成的网络，此时“基地”统一指代后方基地和前沿基地.记需求点集合为I，基地集合为S，补给站备选点集合为J，资源种类集合为P.为简化模型描述，建模时还采用了如下符号.

1）模型参数ωi为需求点i处作战任务的成功完成对完成该次战役任务的重要性度量参数；ζip为资源p对于需求点i处完成其任务的重要性度量参数；Nip为需求点i对资源p的预计需求量；hj为备选点j处的设施容量限制（设施的容量限制是补给站实际容量约束与保障指挥中补给站规模控制的结果）；Uj为当选择在j处建立补给站时，该处可组织使用的配送运力；Us为基地s处可组织使用的运力；q为可建的补给站数量；θp为单位资源p的运力占用比率；μp为单位资源p的容量占用比率；ξip为需求单位i处对资源p的保障时间要求，该参数与需求单位 所在方向的作战强度、该单位的自持能力等有关.本文将其定义为需求单位i的作战指挥人员提出资源p的保障需求后，到必须得到满足时的间隔时间；tsjp，tjip，tsip分别为资源p在基地s与补给站j、补给站j与需求点i、基地s与需求点i间运输所需的时间，该时间包含了资源的装卸时间.

2）决策变量

（1）补给站的选址决策Y.yj＝1时表示开放补给站j，否则取0.

（2）资源配送方案，记为X.按照前文的描述，战役保障中存在多种保障模式，如任务中需求点i的p类资源需求可能通过3种方式加以满足：补给站的前出配送保障，基地与补给站的连续运送保障及基地越级直达保障.因此，为了模型描述和计算求解的简便，本文将这几个物流分别记为xjip，xsjip，sxip.

（3）任务开始时补给站、基地等设施处的资源存储决策Gjp，Gsp

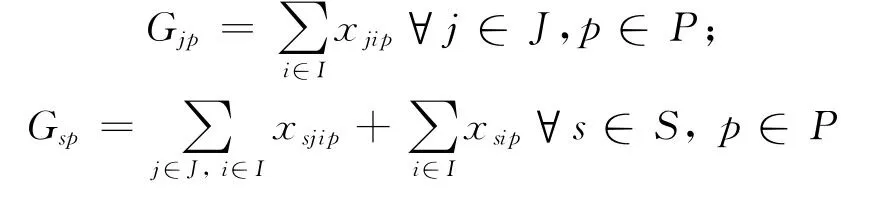
除了资源存储决策外，从资源配送方案还可统计得出各设施处的运力使用方案.

在此基础上，可建立如下优化决策模型

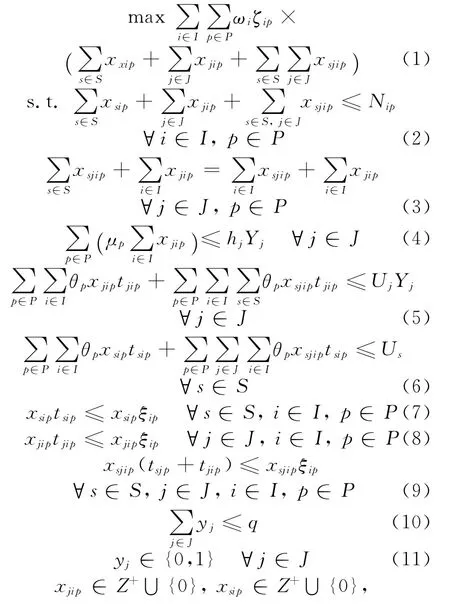
式（1）在于最大化及时运达的重要资源对作战任务的支撑程度，wiζip为需求点i处能及时得到的单位资源p对于完成整个任务的重要性.式（2）为需求点对物资的供需关系约束，到达需求点的资源p不超过其需求总量；式（3）为补给站处的资源平衡；式（4）、（5）分别为补给站处的容量和运力约束；式（6）为基地的运力约束，考虑到基地资源储量相对阶段任务需求量一般比较充裕，本文不考虑基地的容量约束；式（7）～（9）分别为越级保障、前出保障以及逐级连续保障的及时性限制；式（10）为可建的补给站数量约束；式（11）为选址决策变量的二元约束；式（12）为保障过程中资源运送量的非负整数约束.

3 启发式求解框架

在现有的多物资容量有限设施选址问题模型求解方面，主要采用的有基于Benders分解框架的最优化算法［2］、基于分支定界的优化算法［3］、基于拉格朗日松弛的优化算法［4］、遗传算法［5］以及混合Scatter search算法［6］等等，以启发式方法为主.

以上模型经简化后，即为经典的 中值问题，后者已被证明是NP－hard的［7］，因此本文考虑采用启发式方法对模型求解.Marvin等对禁忌搜索算法（tabu search，TS）［8］、模拟退火（simulated annealing，SA）和（genetic algorithm，GA）在求解一般选址问题时的性能表现进行了比较研究［9］，发现TS在解的质量、求解速度以及对问题的适应和扩展能力方面都具有较好的性质，因此本文基于禁忌搜索算法对模型求解.

在给定的选址方案Y下，记选择开放的补给站集合为J0，问题的求解即为对一个在既有的运力约束和时间限制条件下的运输问题的求解，记该子问题的模型为Tr－CLNODM：

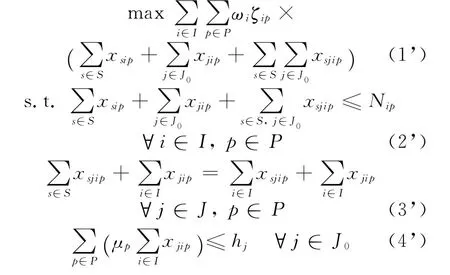
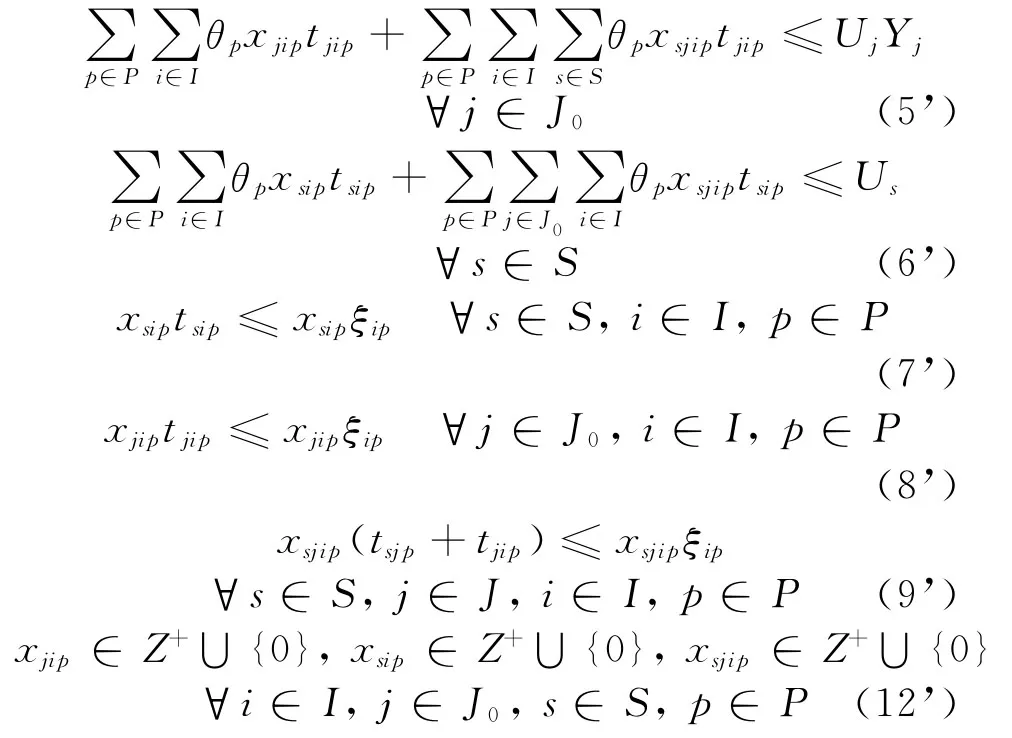
这是一个整数线性规划问题，现有的软件如Lindo6.1和ILOG CPLEX均可对其精确求解.由于ILOG CPLEX允许开发人员将其组件库直接嵌入到C，C＋＋，Visual Basic和Fortran等语言的应用程序中，有利于与启发式求解框架融合.因此，本文基于ILOG CPLEX，采用C＋＋语言实现本文模型的启发式求解框架.

4 计算示例

假设某战役任务阶段，装备保障部门拟动用2个前沿基地，为其保障区域内4个作战方向上的部队进行2类弹药（A和B）的保障.依据作战方案和战役目的，各作战单位所在的作战方向对于该阶段任务的重要性为w1＝0.7，w2＝0.9，w3＝0.5，w4＝0.8.根据作战方案以及预计的作战过程，各需求点对2类弹药可能的需求数量，以及该类弹药对该作战单位完成其任务的重要性如表1所列.同时，由于对抗强度等方面的差异，各需求点对各类资源具有不同的保障反应时间要求，见表2.为了实现更及时、更充足的保障，装备保障部门考虑在该保障区域内建立补给站以前置物资，补给站的备选位置已由战技部门考察确定，且各备选位置处可建的补给站的容量可参考表3.各基地和补给站处可用的运输力量一方面由保障系统分配得到，另一方面来自于就地动员，各设施处可动用的运输力量如表4所列.

由于补给站的开设需要同时配给防卫力量，限于区域内的防卫能力，保障部门在该区域内所能建立的补给站的数量有限（2个）.弹药在基地和补给站备选点间、补给站备选点与需求点间，以及在基地和需求点间的运输时间可见表5、表6.

弹药A和B在各设施处的单位容量占用率μA＝1，μB＝2；单位运力占用率为θA＝0.02，θB＝0.015.实验中对禁忌算法参数取值方式为：禁忌长度TL＝［q／2］，最大迭代次数Nmax＝3×｜J｜，目标函数值持续无改进最大次数Nr－max＝q.将以上参数带入前述的模型和算法，则可求得补给站最优选址决策方案为Y＝（0110）；对应的资源配送规划如图2示，图中各保障流上的数字“x1／x2”分别表示流中资源1与资源2的数量.

表1 弹药需求数量（Nip）／弹药的重要性（ξip）

表2 弹药保障时间要求（ξip）

表3 补给站备选址点容量限制

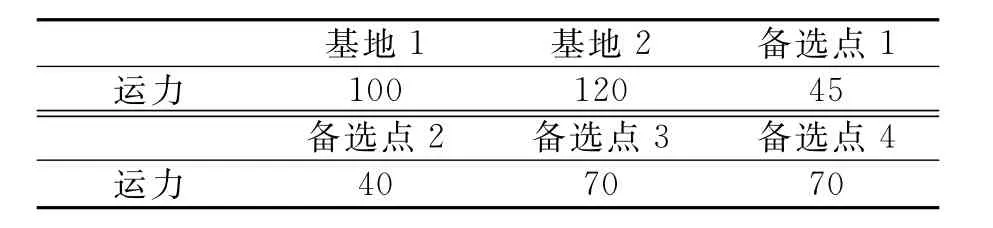
表4 运力约束

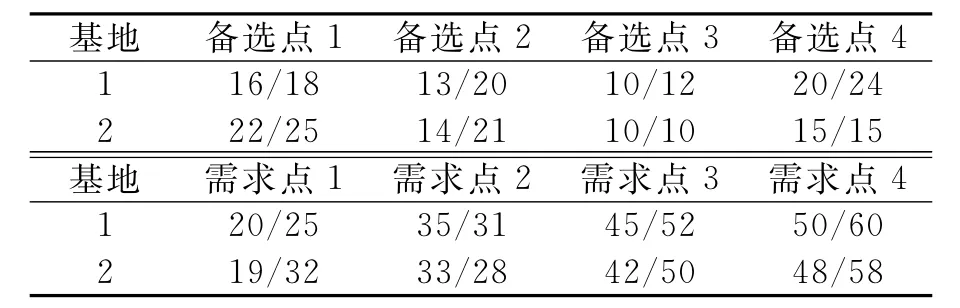
表5 运送时间（tsj（／i）A／tsj（／i）B）

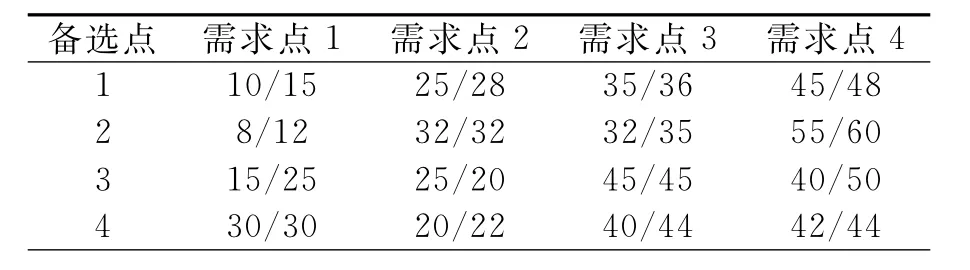
表6 弹药配送时间（tjiA／tjiB）

图2 源配送规划示意图

依据资源配送方案，进而可得各设施处的资源存储方案和容积、运力利用率，见表7.

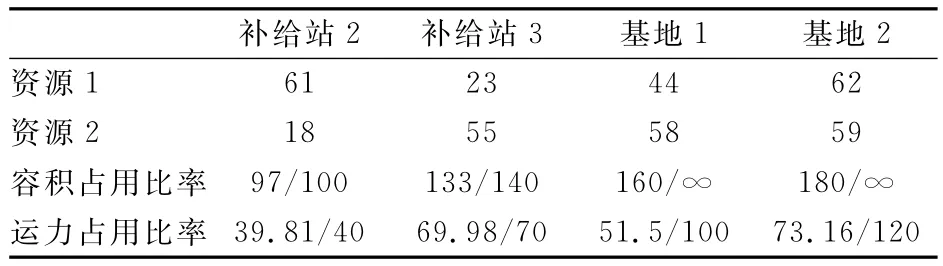
表7 资源存储方案

5 结 束 语

本文主要针对战役供应保障网络的建立方法和模型进行研究，该模型可以用于战时供应保障系统中弹药补给站、卸载点的选址决策以及运力资源的统筹规划，具有理论研究价值和现实意义.本文模型主要是以防御作战模式下的弹药供应保障为背景研究建立的，由于作战模式的差异、资源类别的不同都会给装备保障提出一些新的要求，因此战役供应保障中的问题还有很多，值得进一步探索.

［1］晏湘涛，朱启超，匡兴华.基于共识度决策的军事物流配送中心选址研究［J］.武汉理工大学学报：交通科学与工程版，2010，31（1）：27－30.

［2］Geoffrion A M，Graves G W.Multi－commodity distribution system design by benders decomposition［J］.Management Science.1974，20（5）：822－844.

［3］Marín A，Pelegrín B.A branch－and－bound algorithm for the transportation problem with location of P transshipment points［J］.Computers ＆ Operations Research，1997，24（7）：659－678.

［4］Jayaraman V，Pirkul H.Planning and coordination of production and distribution facilities for multiple commodities［J］.European Journal of Operational Research，2001，133：394－408.

［5］Syarif A，Yun Y，Gen M.Study on multi－stage logistic chain network：a spanning tree－based genetic algorithm approach［J］.Computers and Industrial Engineering，2002，43：299－314.

［6］Keskin B B，HalitÜster.Meta－heuristic approaches with memory and evolution for a multi－product production／distribution system design problem［J］.European Journal of Operational Research，2007，182：663－682.

［7］Kariv O，Hakimi L，An algorithmic approach to network location problems：part II：the p－medians［J］.SIAM Journal of Applied Mathematics.1979，37（3）：539－560.

［8］邢文讯，谢金星.现代优化计算方法［M］.第2版.北京：清华大学出版社.2005.

［9］Marvin A A Jr，Sukran N K，Basheer M K.An empirical comparison of tabu search，simulated annealing，and genetic algorithms for facilities location problems［J］.Int.J.Production Economics.2006，103：742－754.