抛石护岸稳定粒径不同计算公式的对比分析

何 源,张增发,刘曙光,T,atiana Volkova

(1.同济大学土木工程学院,上海 200092;2.镇江市长江河道管理处,江苏 镇江 212001;3.莫斯科大学地理学院,莫斯科)

河道是陆地上一定流域内地面径流和地下径流汇集并宣泄的水路,它由水流和河床这相互作用的两方面构成,水流冲刷着河床,同时河床也约束着水流,它们之间的这种作用是通过泥沙的运动来实现的。当水流条件较强而河床抗冲稳定性较弱时,河床泥沙将被冲刷,严重时可能会产生大规模的崩岸,这不仅造成国土的流失,威胁河道两岸的防洪安全,在通航河道还会对航运的畅通产生不利影响[1-4]。崩岸的发生具有一定的普遍性,据20世纪90年代的统计资料,长江中下游干流河道岸线约长4000 km,其中崩岸段长度达1 500 km,占江岸长度的35.7%。因此,为了防止河道的大量冲刷甚至崩岸,维持比较稳定、有利、生态的河床与岸坡形态,人们往往在岸坡上采取工程措施,将有利河势稳定下来,这其中最主要的就是护岸工程。护岸工程是航道整治中一项最基本的工程,它在防洪、控制河势、保护国土以及规范航道上都起着很重要的作用。

1 护岸概述

传统意义上的护岸工程是采用块石、混凝土或其它材料构筑工程结构或建筑物,通过稳定水流、控制河势,直接或间接保护河岸,并保持适当的水深便于通航的工程措施。在国内已建的护岸工程中,大多使用块石、混凝土等硬质材料,但随着近年来国内外对生态护岸的逐渐强调,以及新技术、新型式的不断涌现,人们更多的关注于使用与生物相容性较好的自然材料[5]。

在各种类型的护岸中,抛石护岸是一种古老的护岸型式,由于其材料来源丰富,施工简单,便于维修养护;抗冲性较强,而且能较好适应河床变形;同时,抛石岸面较为平顺,对水流、河床的自然形态影响较小,因此至今一直得到普遍使用。而随着人们对护岸生态性能的日益强调,块石作为一种天然材料,具有较强的环境友好性和交互性,在今后的护岸工程建设中必将仍会得到广泛采用,或与其它生态材料相配合形成新型的生态护岸型式。因此有必要对抛石护岸结构进行研究,为今后的护岸设计提供依据和参考。

2 抛石护岸稳定性

从稳定的角度,为了保证护岸结构的安全,抛石体必须满足整体和单个块体的稳定性要求,可细分为3个方面进行考虑:①护面层的整体稳定;②单个块体的起动稳定;③块体的结构强度。通常认为,抛石结构的整体失稳破坏是由起初少量块石的失稳而导致的一个链锁破坏过程,可以说,单个块体的稳定性决定了整个抛石结构的稳定性。而对于大部分平原河流来说,流速一般小于3 m/s,水流无法直接将块石击碎破坏,因此单个块体的稳定性问题,实际上就是块石在水流等外力作用下的起动问题。经研究,抛石护岸的破坏首先是从坡脚处开始,由于坡脚处块石和泥沙的不断起动流失,引起上部护面块石的向下滑落从而整体失稳。而且坡脚位于边缘交界处,水流条件相对较强,因此岸坡脚部的防冲对抛石岸坡的稳定至关重要,可以说是抛石岸坡稳定的决定性因素[6]。

2.1 稳定粒径公式

迄今为止,各国研究人员已经对抛石护岸的结构稳定性进行过大量的理论研究和实验,也提出了各家的稳定性计算公式,这其中大部分公式是将单个块体的起动稳定性作为研究对象,并以块石的抗冲稳定粒径作为指标来表述的。研究人员大多以简化的物理模型为依据进行力学推导,并通过大量的实验数据率定参数从而得到实用的计算公式,然而护面块石在水流作用下的稳定情况十分复杂,除了块石自身的重量外,块石间的摩擦、咬合、嵌固等阻碍力也起到了稳定块石的作用,而这些阻碍力或多或少都具有一定的随机性和不可测性。因此,在理论上很难确定精确合理的物理力学模型,得出的计算公式大都属于半理论半经验范畴,有各自的使用范围,不同公式计算出的结果通常也会出现较大差异。鉴于此,本文将对一些国内外典型形式的块石稳定粒径计算公式进行分析对比,试图找出其差异性,并通过引入安全系数来对各公式的计算结果进行评价。现选取以下3个公式:

公式1:《堤防工程设计规范》 推荐公式[7-8]:

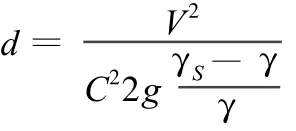
式中d为块石稳定粒径(m);V为水流流速(m/s);g为重力加速度(9.81 m/s2);C为块石运动的稳定系数,水平底坡时取0.9,倾斜坡底取1.2;γS为块石的重率(2.65 kN/m3);γ为水的重率(1 kN/m3)。

公式2:沙漠夫改进公式[9]:

公式3:Shields准则推导公式[10]:

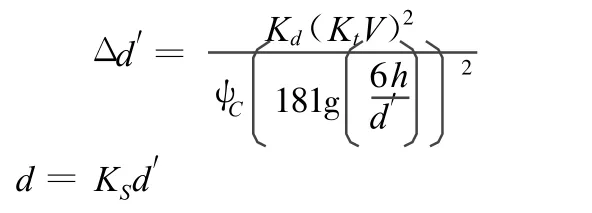
观察上述3个块石稳定粒径的计算公式,除去γS等已知常量外,流速V是各公式中的主要变量,粒径d与V的高次方成正比,可见流速的微小变化会对块石稳定粒径产生较大影响,而对于其它次要因素,各式考虑的有所不同。公式1是根据斜坡上的块石在发生滚动临界状态下的各力矩平衡条件建立的,稳定粒径的计算只与流速 V有关,虽然也考虑到了岸坡倾斜的影响,但这种影响是粗略概化的,只是将岸坡各种倾斜程度划分为水平(倾斜角θ=0)和倾斜(θ≠0)2种情况,并分别取不同的系数C来进行处理;公式2则是以水平河床上的块石起动平衡方程为基础,并考虑坡度影响系数得到的,式中除同样以流速 V作为主要变量外,还体现了水深h和岸坡坡度m的影响;公式3是一种隐式的迭代格式,它由Shields起动判定准则推导出来,考虑的更为全面,除流速V、水深h、坡度影响系数外,将水流紊动程度也作为一项影响系数体现在式中。

2.2 各公式的对比分析

为了反映各变量对稳定粒径计算大小的具体影响,现假定某一平原河段岸坡,选取块石密度,天然休止角,可分别从以下几个不同变量的角度对各公式进行对比分析。

2.2.1 水深因素

令岸坡坡度m=2.5,分别作出水深h=5,10,20m时各式所计算的稳定粒径d随流速V的变化曲线(见图1),并根据斜坡上块石安全系数的计算公式[11]绘出相应的S～ V曲线(见图2)

在不同水深下,各公式的计算粒径均以流速的高次方增长,可见块石稳定粒径对流速的变化非常敏感。而对3幅d～V图进行综合对比,我们发现随着水深的不断增加,公式2和3的计算粒径相应的减小,说明相同情况下块石被水流覆盖越深,其所需的稳定粒径越小,公式1的计算曲线则没有变化,没有考虑水深改变的具体影响,而是采用了偏安全的系数进行估计,观察上图,在流速较小时,公式1的计算粒径要大于公式2和3的计算结果,而一般平原河流流速较小,因此在实际工程中使用公式1可以得到偏大的结果。

图1 不同水深下稳定粒径与流速关系(d～V)曲线

图2 不同水深下安全系数与流速关系 (S～V)曲线

而从安全系数的角度分析,水深较小时,在流速较大区,公式3算出的稳定粒径很大,然而相应的稳定系数却较小,甚至小于公式1和2计算出的较小粒径的安全系数,这说明在斜坡上的块石,粒径大小并不是其明确的稳定指标,这是因为块石自重沿斜坡面的分量也是诱使块石失稳运动的因素之一。因此在对岸坡进行块石护岸时,在满足稳定性要求时,块石可尽量选取较小的粒径。

2.2.2 坡度因素

再令水深h=10 m,分别作出岸坡坡度m=1.5、2.0、3.0时各式所计算的稳定粒径d随流速V的变化曲线 (见图3),并绘出相应的 S～V曲线 (见图4)。

图3 不同坡度上稳定粒径与流速关系(d～V)曲线

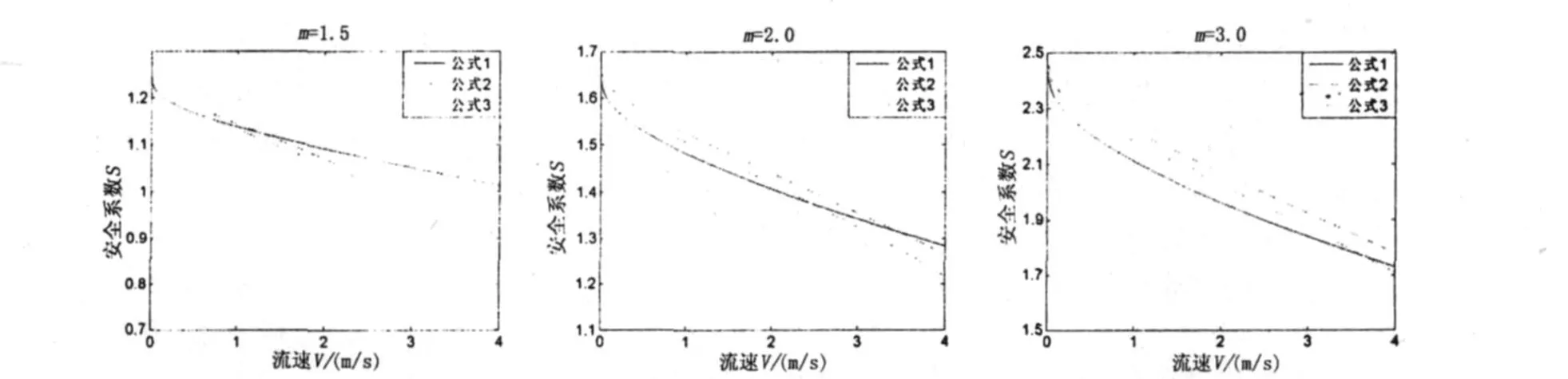
图4 不同坡度下安全系数与流速关系 (S～V)曲线

同水深因素影响类似,块石所处的岸坡越缓,其越容易稳定。在规范推荐的坡度1∶1.5～1∶3.5的范围内,m=1.5是其中较陡的情况,此时公式2和3的计算结果在流速较大时S＜1,块石不稳定,而公式1计算粒径相应的安全系数虽也有所降低,但仍能满足S＞1的稳定条件。随着m的增大,坡度逐渐变缓,各公式的计算粒径有减小的趋势,而安全系数却不断增加。

3 结 语

经过上述分析,可以看出,《堤防工程设计规范》 推荐使用的公式1可适用于各种水深、坡度以及流速的情况,其计算结果均能保证一定的安全系数,而且与其它2个公式相比较,公式1计算粒径的安全系数比较稳定,变化幅度较小,尤其在条件偏危险时 (水深小、坡度陡)仍能按一定的安全系数保证护岸块石的稳定性要求。而在水深、坡度等条件偏安全时,公式1的计算结果偏大,反而降低了护岸的安全系数,因此笔者建议,在水深较大、坡度较缓等条件下进行护岸设计,在使用公式1确定块石稳定粒径时,应参考公式2和3的计算结果,乘以1个粒径折减系数,从而得到一个更为合理的结果。

[1]岳红艳,余文畴.长江河道崩岸机理[J].人民长江,2002(8):20-22.

[2]徐永年,梁志勇,王向东,等.长江九江河段河床演变与崩岸问题研究 [J].泥沙研究,2001(4):41-46.

[3]王俊.安徽省长江护岸工程[J].人民长江,2002,33(8):18-19.

[4]亨普希尔.河渠护岸工程 (方案选择及设计导则)[M].北京:中国水利水电出版社,2001.

[5]钟春欣,张玮.传统型护岸与生态型护岸[J].红水河,2006,25(4):136-139.

[6]应强,张幸农,张思和,等.不同粒径块石及其组合的护岸效果 [J].水利水运工程学报,2009(2):44-49.

[7]中华人民共和国交通部.堤防工程设计规范 [S].北京:中国计划出版社,1998.

[8]余文畴.抛石护岸稳定坡度与粒径的关系 [J].泥沙研究,1984(3):69-74.

[9]赵搏天,胡应娜.抛石护岸设计方法简析 [J].黑龙江水利科技,2009,37(4):301-302.

[10]张明光.抛石护岸工程设计中块石粒径的确定[J].人民长江,2003,34(2):24-25.

[11]迈克尔·A.史蒂文斯,达利尔·B.西蒙斯,加里·L.刘易斯,等.抛石护坡的安全系数 [J].广西水利水电,1979(2):56-71.