基于主成分分析的BP神经网络及其在需水预测中的应用
2010-07-06龙训建
龙训建 钱 鞠 梁 川
水资源是人类社会生存与发展中不可替代的重要自然资源及生态环境系统的基本要素[1]。随着人口增长和工农业生产的发展,水资源供需矛盾日益加剧,所面临的水危机日益严重;加上社会经济用水挤占了生态用水,使得天然河湖萎缩、消失,土地荒漠化等,造成生态环境失调,严重阻碍了经济社会的持续发展[2~4]。用水量的高速增长和水资源的短缺使得水资源规划和用水系统的优化调度越来越重要,进行需水量预测则成为了实现水资源规划和管理的有效手段之一[5]。作为全国首批节水型社会试验县之一,近年来,甘肃省瓜州县经济建设快速发展,产业结构战略性调整,对水资源需求、开发和利用提出了新要求,因此,确保水资源的高效利用成为了经济和社会可持续发展的重要保证。
国内外关于需水预测研究历史悠久,但由于近年来水资源与经济社会之间的矛盾愈加突出,对于水资源需求的研究方式也呈现多样化发展趋势[6]。各种计算模型、模拟程序(如定额预测、回归分析预测、指数法预测、灰色模型预测、神经网络模型等)都尝试应用于需水预测方面的研究[7~9]。选择合理的需水预测方法,不仅可以增加水资源配置研究工作的实际操作性,还可得到更符合社会经济发展趋势的结果。无论采用何种需水预测模型,都需要对影响因子进行筛选。因子选择过少,必然会影响预测结果的准确性;因子过多,会使网络训练复杂化,可能陷入局部优化问题,难以得到全局优化解。人工神经网络是当前国际学术界十分活跃的前沿研究领域,具有广泛的应用领域。本文首先应用主成分分析法确定影响总需水量的主要因子,然后以此构造BP神经网络的输入样本,进行BP神经网络的训练与预测,以提高模型的学习和泛化能力。
1 研究方法
1.1 主成分分析法
在相关影响因子分析中,主成分分析是将多个指标化为少数相互无关的综合指标的统计方法。其基本思想是通过变量的相关系数矩阵内部结构的研究,找出能控制所有变量的少数几个随机变量去描述多个变量直接的相关关系[10]。从数学角度而言,这属于降维处理技术。对于有n个样本的p个变量的原始资料矩阵X(n×p),进行主成分分析过程为:
a.对原始数据矩阵 X(n×p)标准化处理,得到新的数据矩阵

b.建立标准化后的p个指标的相关系数矩阵R

d.计算贡献率em和累计贡献率Em。

e.计算主成分荷载zm。它表示主成分与变量之间的相关系数。

1.2 BP神经网络需水预测
人工神经网络是通过数学方法对人脑若干基本特性进行的抽象和模拟,是一种模仿人脑结构及其功能的非线性信息处理系统[11,12]。经过半个多世纪的发展,由于各种网络结构和算法系统的产生,已逐渐发展成较为完善的人工神经网络理论体系。BP神经网络是该技术中应用最为广泛的一种,其特点有[11,13~15]:自适应、自组织、自学习的能力、非局域性和非凸性的突出优点。正是这些特点使得该方法已经解决了许多实际问题,其生命力也恰恰在于广泛的实用价值[11]。为了能够更好地泛化全局最优问题,许多学者提出了很多针对性的办法,主要包括以下三方面的改进[11]:一是提高网络的训练速度;二是提高训练精度;三是避免落入局部极小点。
通常情况下,需水预测BP神经网络模型包括输入层、隐含层和输出层3部分。3层BP神经网络模型的理论计算步骤大致为:
第1步,将样本的输入、输出变量归一化处理,即将所有数据转化至[0,1]之间。给每个连接权值wij,vjt,阈值与赋予区间(-1,1)内的随机值。
第2步,用输入样本 xk=(x1k,x2k,…,xnk)、连接权值和阈值θj计算隐层各单元的输入,然后用通过传递函数计算隐层各单元的输出bj。

第3步,利用隐层的输出bj、权值 vj和阈值γt计算输出层各单元的输出Lt,然后通过传递函数计算输出层各单元的实际输出Ct。

第4步,利用网络目标向量 Tk=(y1k,y2k,…,yqk)与网络的实际输出Ct,计算输出层的各单元训练误差dtk。
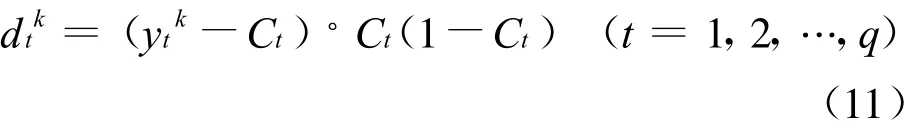
第5步,利用连接权值vjt、输出层的训练误差dt和中间层的输出bj计算隐层各单元的训练误差ejk。
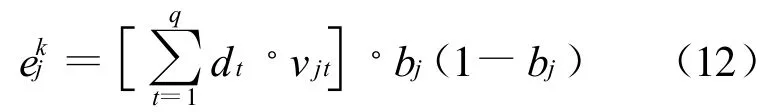
第6步,利用输出层各单元的训练误差dtk与隐层各单元的输出来修正连接权值阈值。

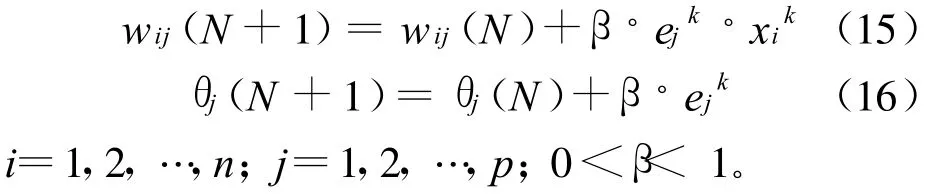
2 结果与分析
2.1 确定需水量主要影响因子
选取瓜州县1988~2007年总需水量序列资料和区域社会经济资料作为基础数据(部分统计结果见表1),将总需水量作为主成分回归分析的因变量,国内生产总值、工业产值、农业总产值、人口总数、耕地面积、播种面积和大牲口数量7个因子作为自变量,应用SPSS分析软件的主成分分析功能,求得相关系数矩阵R,结果见表2。从表2可知,7个因子存在不同程度的相关性。其中,国内生产总值与农业总产值的相关系数为0.981,国内生产总值与人口总数、人口总数与农业生产总值的相关系数均为0.965。由此可提取出彼此独立的变量,筛选有代表性的因子构造BP神经网络的输入样本。
根据表2的相关系数矩阵和主成分分析步骤b~d,得到所筛选7个因子的相关系数矩阵R的特征值和贡献率计算结果,列于表3。从表3可以看出,第1个因子的贡献率为80.987%,前2个因子的累计贡献率达到93.193%,由此表明这2个因子基本上代表了原来7个因子93.193%的信息。由于通常情况下,因子累计贡献率达到90%以上时就可以反映相关因子的影响,因此,可确定所选7个因子中的前2个因子代替原变量。
由式(6)计算表3中前2个因子的荷载矩阵,结果见表4。由表4可看出,国内生产总值、工业产值和农业总产值对第一主成分的相关系数都超过了0.95,相对其他因子贡献最大;大牲口数对第二主成分贡献最大。因此,选用国内生产总值、工业总产值、农业总产值和大牲口数4个因子作为主成分,并以此构造BP神经网络输入样本。
2.2 改进的BP神经网络
2.2.1 模型的建立
建立BP神经网络需水预测模型,首先要确定输入层、隐含层和输出层的节点数。输入层的节点数为影响水资源需求量的因子数。通过主成分分析法,与瓜州县年总需水量有显著关系的主要影响因子包括:国内生产总值、工业总产值、农业总产值、大牲口数,由此可得出输入层为4个节点。各因子1988~2007年的统计结果见图1。预测对象为年总需水量,因此输出层为1个节点。隐含层节点数的确定采用试算法,选取训练与测试结果误差最小所对应的隐含层神经元数作为最后确定的隐含层节点数。

表1 瓜州县典型年需水量及社会经济统计表Table 1 Water demand&social economy statistics of Guazhou,Gansu

表2 各自变量的相关系数矩阵Table 2 Correlation coefficients matrix of variables

表3 主成分特征值和贡献率Table 3 Eigenvalues and contribution rates of principle constituents

表4 主要因子的荷载矩阵Table 4 Load matrix of main indices
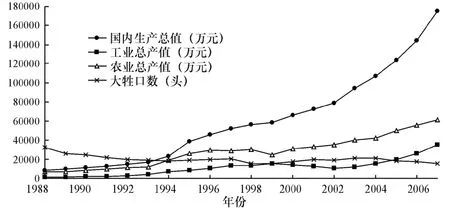
图1 四个主成分因子年际变化序列Fig.1 Variation of annual distribution of the four main indices
2.2.2 模型求解
通常情况下,为了加快训练过程中的收敛速度,需对原始数据进行归一化处理,具体计算公式为:

从样本数据中选取1988~2004年样本进行网络训练,2005~2007年的已知样本对网络进行检验。同时,选取适当初始学习率η=0.9,运算次数10 000,允许精度E=0.05,训练函数采用Polak-Ribiere共轭梯度法的Purelin函数。经试算,在隐含层神经元数为8时,训练效果最佳,预测值与实际值对比结果见图2。采用此次训练结果进行样本检验,检验结果及检验误差见表5。
从图2可知,各年需水量预测值与实际值拟合精度较高,曲线基本重合。表5中检验结果表明,绝对误差小于±0.05×109m3,在允许误差范围内。显然,这种基于主成分分析法构造BP神经网络的输入矩阵的训练过程误差较小,取得的预测结果也令人满意。
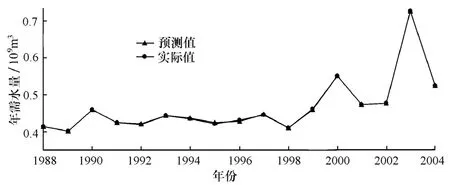
图2 BP神经网络预测结果Fig.2 Prediction outcome of BP neutral networks
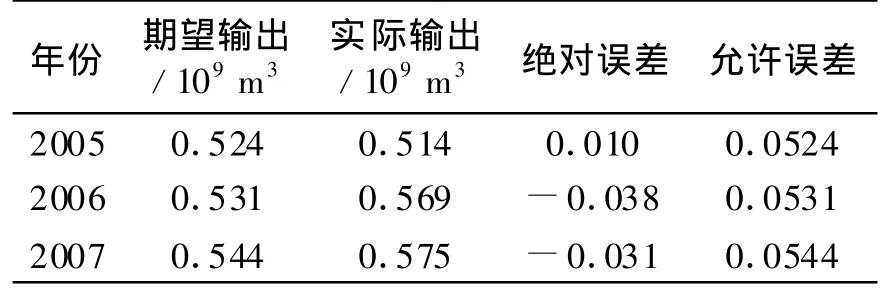
表5 总需水量预测检验结果Table 5 Testing outcome of total water demand prediction
3 结论
a.通过主成分分析,确定了影响瓜州县需水量的主要因子,包括国内生产总值、工业总产值、农业总产值、大牲口数。这4个因子的累计贡献率达到93.193%。
b.由于神经网络模型具有局部逼近的特征和较强的非线性映射能力,因此它能够较好地模拟具有较强非线性变化特点的需水预测问题。基于主成分分析的BP神经网络简化了网络输入样本,消除了网络输入之间的相关性,降低了网络的输入层数,改善了程序执行效率,从整体上提高了网络的性能。最终取得了良好的预测结果。
[1]王浩.我国水资源合理配置的现状和未来[J].水利水电技术,2006,37(2):7-14.
[2]郑度.中国西北干旱区土地退化与生态建设问题[J].自然杂志,2007,29(1):7-12.
[3]朱丹果,上官智锋.西北地区水资源可持续发展的障碍及解决策略[J].环境科学与管理,2007,32(6):51-53.
[4]沈福新,耿雷华,曹霞莉,等.中国水资源长期需求展望[J].水科学进展,2005,16(4):522-525.
[5]吕智,陈文贵,丁宏伟.干旱区内陆盆地水资源的合理配置——以甘肃省高台县为例[J].水资源保护,2005,21(6):45-48.
[6]王浩,游进军.水资源合理配置研究历程与进展[J].水利学报,2008,39(10):1168-1175.
[7]和刚,吴泽宁,胡彩虹.基于定额定量分析的工业需水预测模型[J].水资源与水工程学报,2008,19(2):60-63.
[8]刘俊萍,畅明琦.径向基函数神经网络需水预测研究[J].水文,2007,27(5):12-16.
[9]甘治国,蒋云钟,鲁帆,等.北京市水资源配置模拟模型研究[J].水利学报,2008,39(1):91-95.
[10]张妍,尚金城,于相毅.主成分-聚类复合模型在水环境管理中的应用——以松花江吉林段为例[J].水科学进展,2005,16(4):592-595.
[11]苑希民,李鸿雁,刘树坤,等.神经网络和遗传算法在水科学领域的应用[M].北京:中国水利水电出版社,2002.
[12]高隽.人工神经网络原理及仿真实例[M].北京:机械工业出版社,2007.
[13]凌和良,桂发亮,楼明珠.BP神经网络算法在需水预测与评价中的应用[J].数学的实践与认识,2007,37(22):42-47.
[14]张雪飞,郭秀锐,程水源,等.BP神经网络法预测唐山市需水量[J].安全与环境学报,2005,5(5):95-98.
[15]董长虹.Matlab神经网络与应用[M].北京:国防工业出版社,2007.
