凯恩思定律成立的条件和局限——兼析某些误解和曲解

○韦沛文 韦 超 （中山大学新华学院 广东 广州 510275）

一、引言

关于生产和收入决定于总需求的理论，可说是凯恩思经济学说的核心（高鸿业，1996）。由之推导出来的乘数理论，影响着许多青春学子和经济学家们的思维，使人们产生了消费越多甚至越铺张浪费，社会产出或收入就会越多，社会就越富裕的错觉。例如在消费系数β=0.8时，“投资增加100亿美元，收入增加500亿美元，增加的收入是增加的投资的5倍”（同上）；“政府购买支出若增加200亿美元，则国民收入可增加1000亿美元”（同上），等等。似乎只要β足够大，增加少少的投资，收入就会大大的增加，政府的开支越多，产出也会越多，不管政府支出是用于投资还是铺张浪费。由于凯恩思的整套理论点缀了不少看似严密的数学推导，着实吓唬了不少人，除少数教材提出过某些警告，认为“需求决定供给的理论决不可乱用”（同上）外，大多是不加分析批判地全盘照搬。本文作者经过深思熟虑的研究分析，发现需求决定产出或供给的凯恩思学说之核心，完全是一种对产出数学方程式的误解或者说曲解。

二、必须和可能是两码事

y=c+i=（α+i）/（1-β），本意是某期产出或收入计划用于消费部分为c，用于投资部分为i，且在c=（βy+α）的刚性约束情况下该有的必须的产出或收入。因为y=（α+i）/（1-β）仅仅是方程组 y=c+i，c=（βy+α）即方程 y=（βy+α）+i在数学上成立的必要条件，并非实际经济有能力一定产出这么多的证明或充分条件。

为方便进一步说明y=（α+i）/（1-β）仅仅是方程y=（βy+α）+i在数学上成立的必要条件，设α＝0，则y＝c+i=βy+i，于是有：

若β＝0.8，则消费和投资各占收入y的0.8和0.2倍，消费是投资的4倍，故：

当i=1，c必须为4，得y＝5；（其意思实际是只有y达到5了，才可能在满足消费占0.8的刚性约束下，投资达到i=1，下同。）

当 i＝3，c必须为 12，得 y＝15。

若β＝0.99，则消费和投资各占收入y的0.99、0.01倍，消费是投资的99倍，因此：

当 i=1，c必须为 99，得 y＝100；

当 i＝500，c必须为 49500，得 y＝50000。

以上结果符合y=i/（1-β），且△y=△i/（1-β）。但以上仅说明由于方程是y＝c+i=βy+i，βy与i有一定的倍数关系，故i的某一变动βy就要变化为确定的倍数，从而y变动到一个再加1的倍数。y=i/（1-β）或△y=△i/（1-β）是方程y=βy+i保持成立的必要条件，是一种纯数学关系，这和Y＝X＋Z，当Z=4X时，X增加1，Z必然要增加4，从而Y必然要增加5一样，是一种纯数学关系，并非经济运行上的必然。经济并不会你对方程加了“均衡产出”几字它就一定会按你的“意想”达到“均衡”了。一定投资和消费下，经济产出多少是与科学技术水平、资本用量、劳动投入等因素密切相关的，例如柯布－道格拉斯方程y=PAKaLb就是一种可能的产出函数，当A、K、L（分别为技术、资本、劳动，P为产出量的平均单价）都有充分的余量时，在市场机制的自动调节的作用之下，才有可能产出满足所计划的消费和投资需求的产出数量y=（α+i）/（1-β）。应该把必要性y=（α+i）/（1-β）和可能性（如 y=PQ=PAKaLb之类的生产函数）联合求解，才能得到需求和供给均衡的产出y。

可见，消费比例越高，产出或收入就会越高、投资乘数越大的说法，是对y=c+i=（βy+α）+i的误解或曲解，是把必要性当作必然性或充分可能性了。正确的说法应是：要满足y=（βy+α）+i，产出 y必须等于（α+i）/（1-β），从而投资乘数 k=△y/△i将等于1/（1-β）。在消费系数β刚性的前提下，是产出的多少决定着能投资多少，或者说，要实现投资多少，就必须要求产出能达到多少倍，并非因为消费而使产出必然会比投资增加多少倍。

必须和可能是两码事，不能混为一谈。当β较小时，比如β＜0.7左右，总收入有30%左右用于投资，生产能力再生充足，在需求的拉动下，保持投资乘数k=1/0.3=3.3倍是有可能的，但要说β增加到0.99，此时k=1/0.01=100倍也能实现，增加投资1万就能增加产出或收入100万，就是没文化的大老粗，也不会相信，除非是赌场或彩票市场，有时会有这样的奇迹。消费的比例过高，投资无以为继，资本存量将逐渐耗尽，产出将急剧下降。可见必要和可能，虽一词之差，却可能差之毫厘，失之千里。高鸿业等已经正确地认识到“对于一个处于经济危机中具有大量闲置生产能力的资本主义国家而言，凯恩思定律是有一定现实基础的。然而，就正常状态……一味强调增加需求，结果可能不是生产增加，而是物价上涨。因此，需求决定供给的理论切不可乱用。”（高鸿业，1996）

经济运行的实际情况是，每年的固定资产投资就要占GDP的1/4到2/5（这可从许多年鉴上查到），加上流动资产投资，每年投资占GDP的1/3到1/2或更多。例如广东省1997—2004的8年间，仅固定资产投资累计29507.44亿元，GDP累计84413.84亿元，考虑流动资产投资也不会太少，产出与投资之比最多就是2，从而可算得β＝0.5，K=2，i=42206.92亿元。这能说是广东人太蠢了把太多的钱用来投资而不是用来消费吗？如果我们在凯恩思们的教唆下，把消费系数提高到0.9或以上，请你告诉我，GDP累计是会达到42206.92亿元的10倍还是连2倍即84413.84亿元也不能实现呢？我敢肯定是后者。

三、凯恩思定律成立的条件和局限

下面以需求函数y=（α+i）/（1-β）和生产函数Y＝PAKaLb导出凯恩思定律成立的条件。

假设需求y是1年内的需求，（因为生产函数Y＝PAKaLb通常是以年为周期）。要使产出达到或超过需求y=（α+i）/（1-β），生产能力Y必须大于等于y，即：

K0、L0分别为上期末即本期初的资本和劳动力，i为本期投资，△K、△L为本期增加的资本和劳动投入。因为本期一定有资本折旧，故投资i补偿折旧后的余额才是本期的△K。设d为资本资产的年折旧率，则△K＝i－K0d，即△K并不等于i。但由（1）式已可说明：i越大，（1）式的第2项的分子越大，从而第2项的值越大，β值越小，两者负相关，即β的值需随i的增加而减小；生产能力PA（K0+△K）a（L0+△L）b越大，（1）式第2项的值越小，β值可大些。这说明了以下几个问题。

其一，要使在 1年的时间内达到 y=（α+i）/（1-β），β 不能任意大，有一个上限，受投资i和生产能力AKaLb制约。投资越大或生产能力越小，β就必须越小，反之可越大，并非凯恩思们片面地从 y=（α+i）/（1-β），k=1/（1-β）所鼓吹的那样，i越大和β越接近于1产出就越多。这一法则其实已暗含于y=c+i之中，生产能力从而产出y总是有限的，i增大了，c就小了，因之消费比例系数β要相对小些。对于发展中国家来说，只有限制消费和浪费，增加投资以积累资本K，同时增加劳动L的投入，提高科技水平A，才能使生产能力和产出不断提高，经济不断发展，从而提高消费份额β，而不是反过来用增加消费的办法发展经济。

例：若生产能力 PAK0aL0b＝8000，α＝1000，i＝600，可计得β＜＝0.8。如果下一期投资增加到i＝700，假如由于投资增加的100刚好够补偿折旧，劳动力又没有增减，则生产能力仍为8000，可计得β＜＝0.7875。若i=0，即本年不投资，其他条件不变，则可计得β＜＝0.875。此即生产能力＝8000，α＝1000下最大的消费系数了。3组数据表明i和β确是负相关。

其二，在生产能力有余量的条件下，i和β确实越大越好，这才是消费决定供给的凯恩思定律成立的条件。对发达国家，由于生产能力往往过剩，提高投资和消费系数β都可增加产出，从而使经济进一步发展，人民生活水平进一步提高。但生产能力（A、K、L）总不是无限的，消费决定产出终归有一个度，β必须小于等于1－（α+i）/PA（K0+△K）a（L0+△L）b。20世纪30年代的经济大萧条时期的西方，正好满足了这一条件，凯恩思定律的运用卓有成效，从而迷惑了许多人，使消费决定供给的论调泛滥成灾，过渡消费催生了今天的经济大危机。

由年产能Y=PA（K0+△K）a（L0+△L）b可知，在劳动力不增加，△L＝0，技术水平A假定也差不多的条件下，Y=PA（K0+△K）a（L0）b，本年最大产出决定于△K＝i－K0d。

若△K＝0即i＝K0d，投资仅能补偿资本资产损耗即都是作为资产的重置投资，Y=PA（K0）a（L0）b与上年持平，是为马克思所说的简单再生产情况。此时β＜＝1－（α+K0d）/PA（K0）a（L0）b＝β0；若i＞K0d，Y=PA（K0+i－K0d）a（L0）b比上年增产，是为马克思所说的扩大再生产情况，此时β＜＝1－（α+i）/PA（K0+i－K0d）a（L0）b，上面已证β随i的增大而要下降一些，小于β0，但消费的绝对量是有所增大的，因为y增加了；若i＜K0d，Y=PA（K0+i－K0d）a（L0）b＜PA（K0）a（L0）b比上年减产，是为萎缩再生产情况。上面已证只要满足 i＞[αa－（1-d）K0]/（1-a），β随i的减小反可有所增大，会大于β0，但消费的绝对量是减小的，因为y减小了。

这些规律可能可对当前的迪拜债务危机做出解释，政府大规模负债投资（负债1000多亿美元，已到期要偿还的约600亿），消费系数本应要有所降低，才能使人们因投资增加而增加的收入这部分转变为购置生产出来的房地产的消费支出，使开发商和政府得以还贷。但由于人们的消费倾向的隋性，其他生活用品的消费系数没有降低，由于收入的增加而按原来的消费倾向βy购买了更多的生活用品，购买房地产这部分就相对货币不足了，从而投资不能按计划速度回收。

这些规律甚至也可对美国的次贷金融危机做出解释，房地产泡沫使房地产投资i扩张，消费者按揭买房即是α增大，（因为 α 是收入为 0时的负债消费），β＜＝1－（α+i）/PA（K0+i－K0d）a（L0）b将要求小于β0更多一些，使能用较多的收入还债，但美国人的超前消费习惯加上凯恩思需求决定供给定律的影响，使美国人从普通老百姓到经济专家们均没有负债投资和消费的风险意识，消费倾向β和α有增无减，终于出现了消费者无钱还贷从而使整个经济的资金链断裂而产生金融和经济危机，波及全世界。

这些就是以年为限的不同情况下凯恩思定律成立的条件和局限。在y=（α+i）/（1-β）小于产能的情况下，增加消费可以使更多资金回到供给方，可以保证投资从而增加产出；增加投资可以扩张产能增加产出，从而增加可消费的绝对量，但消费系数要下降；减少投资虽可提高消费系数，但生产会萎缩，从而减少可消费的绝对量。β和i不能同时增大，更不能无限制地增大。

其三，在供给和需求这一对立统一体中，它们既互相促进又互相制约，但供给始终是矛盾的主要方面，对产出和经济发展起主导作用。需求决定供给的凯恩思定律把矛盾的主次方面颠倒了，过分地强调了需求对供给的拉动作用，忽视供给对消费的促进和制约，是不符合实际的片面的观点。其直接负面影响就是鼓励个人和政府的巨大浪费和赤字。在生产能力足够的前提下，浪费（例如网上所说的，等我有了钱，买4个包子，吃两个丢两个之类）虽也能增加产出，拉高GDP，但其实质是消耗了社会资源却不增进社会福利，消耗了社会资源必然要影响经济的后续发展从而影响后续的社会福利，这也是片面强调消费或需求决定供给这一论调的严重负面效果之一。

四、关于达到均衡产出的过程

y=（α+i）/（1-β）是凯恩思理论在一定的投资和消费水平下应达到的产出水平，西方学者认为这一水平不是一步到位而是经无限次的产出而逼近的（高鸿业，1996），并提出本期消费是上期收入的函数，把y=（βy+α）＋i改造为yt=（βyt-1+α）＋it。此种想法的错误在于以下几方面。

其一，对于以日或月为周期的较短时限作为一“期”的情况，本期消费数量由上期收入yt-1所决定有一定道理，但本期所消费的产品也可能一部分或大部分甚至全部是上期所生产的，本期的投资也多是上期的收入中拿出来的，因此从“本期支出＝上期收入”考虑，用 yt-1=（βyt-1+α）＋it即yt=（βyt+α）＋it+1更为合理。从而：yt=（α+it+1）/（1-β），这样，当 y0＝8000，α＝1000，β＝0.8，i0＝600，i2＝i1＝700 时，仍应计得 y1＝8500，而不是按yt=（βyt-1+α）＋it的8100。当然，如前面所述，这8500仍是方程成立所必须而非实际能产出的产量和收入。

其二，如果以季、年等较长的时间为一期，此时往往是本期的收入有相当大的部分会用于本期的消费和投资，从而对本期消费和投资多少有决定性的作用，yt=（βyt-1+α）＋it就更不科学了，还是yt=（βyt+α）＋it即凯恩思原来的方程y=（βy+α）+i更合理。

其三，按yt=（βyt-1+α）＋it式计算，需经无限“期”后才能达到产出 8500的所谓均衡产出，y=（α+i）/（1-β）还有什么意义呢？如果以日或月为周期的较短时限作为一期，经许多“期”后产出能接近y=（α+i）/（1-β）也许还可以接受，而以季、年等较长的时间为一期，需经无限“期”后才能达到均衡产出y=（α+i）/（1-β），这种理论对实际经济运行情况就没有什么指导价值。

其四，y=（α+i）/（1-β），△y=△i/（1-β）的达到其实是这样的：当假设的二部门经济体内的生产部门决策者计划下期把投资增加△i变为i1＝i0＋△i时，不管这个i1是有部分是上期储蓄所留下的，还是部分由外部借入的，还是部分或全部由本期收入投入去的，本期开始有产出后，都要把产出的大约（1-β）倍的部分用于本期投资或储蓄（留用于下期投资）或还贷，约βy用于消费，直到本期投资达到i1＝i0＋△i，本期的产出有（1-β）y-α用于本期的投资＋储蓄＋还贷，消费又达到（βy+α）为止。此时本期累计的产出就达到y1=（βy1+α）＋i1即y1=（α+i1）/（1-β）了，这时才算本期的结束。但此时所用时间长短是不一定与上期相同的，要视所增加的投资△i和生产能力的大小而定。若上期产能已是用到最大了，本期生产能力不变即与上期一样（即投资i1只够补偿折旧，劳动力也已充分就业不增加了）的话，则：

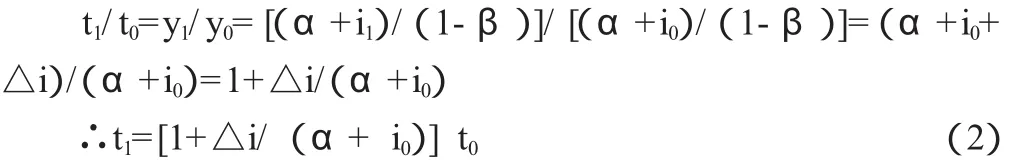
例如，对 α＝1000，i0＝600，i1＝700 的情况：

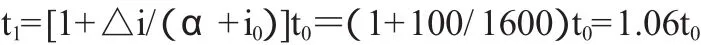
可见，增加投资后本期只要比上期多生产百分6的时间，就达到了所需的均衡产出8500，并不是书上所说的无限“期”。事实上，按（高鸿业，1996）所举例的无限期后的累计总产出，因为每一期的产出均大于8000，已经是早大于n×8000（n为期数）了，累计投资也比开始时的600增加了[（n×700）－600]这么多了（因为每期均投入700）。可见，所举的yt=（βyt-1+α）＋it例子，只能说是“在每个周期相等的连续n期内都比基期追加相等的投资△i，经无限期后，才会使此时一期内的产出比基期产出增加△y=△i/（1-β），其中△i＝in-i0是第n期投资比基期投资的增量”。这和 y=（α+i）/（1-β），△y=△i/（1-β）是不同的两码事，y=（α+i）/（1-β），△y=△i/（1-β）说的是：要满足y=（βy+α）+i，产出 y必须等于（α+i）/（1-β），从而投资乘数k=△y/△i必须等于 1/（1-β）。y=（α+i）/（1-β）是没有规定产出“期”的时间长短的，只要产出达到了（α+i）/（1-β），y=c+i=（βy+α）+i就成立了。由（高鸿业，1996）所举之例真可说明“这是一个例子，它向我们表明：此种证明（指凯恩思们对其理论的许多堂而皇之的证明）没有多少价值。本书以及西方经济学中的许多证明都是如此。”（高鸿业，1996）的说法是完全有根据的。可见我们确实不应盲目迷信西方的经济学理论。

事实上，在消费系数β不是太高，即能保证投资占产出的一定比例，从而增加投资能超过原有资本存量K0的折旧损耗的条件下，增加投资后生产能力会比上期提高，产出y达到（α+i）/（1-β）所需的时间会更短些，推导如下：

设年生产函数为Y=PAKaLb，则基期达到产出y0=（α+i0）/（1-β）所需时间为：

其中假定A，L不变，仅K增加了△K，△K=i0－资本折旧额＝净投资。

由于 a＞0，[1+△K/K0]＞1，故分母（1+△K/K0）a＞1，从而t1＜[1+△i/（α+i0）]t0。（见（2）式）。说明达到所要求的产出的时间比未考虑生产能力提高的情况确实少了一些。

由 t=y/（PAKaLb）＝（α+i）/（1- β）/（PAKaLb）年可看到，在产能（PAKaLb）一定的条件下，β越大，达到所需的产出（α+i）/（1-β）的时间t就越长。但生产期很长才达到所需的产出（α+i）/（1-β），其平均年产出量则比消费系数β较小时要低，消费就不是拉动经济而是阻碍经济的增长了，消费系数β虽然高，每年实际得到的消费量却少。上述的i＜K0d的情况就是如此。

这些就是凯恩思定律的真实意义：当不限定生产周期的长短时，理论上，消费系数可以无限接近于1，投资i也可以很大；但若限定了产出时间，如1年，则消费系数的最大值和投资有一定的关系，不能是任意大小。

其五，宏观经济学教科书常以一笔初始投资i会转化为收入i，因为此收入i的β倍即βi又用于消费支出，从而又形成新一轮的收入βi，这一收入βi的β倍即β2i又用于消费支出，从而又形成下一轮的收入β2i……如此经无限次收支后，总的收入y=i+βi+β2i+……+βni=i/（1-β）作为均衡产出的实现过程和凯恩思定律确实成立的有力证明（高鸿业，1996）。

其实，y=i+βi+β2i+……+βni=i/（1-β）与其说是产出或收入实现的过程，不如说是货币流通的过程，它表示的是从银行流出的一定的货币量i，在居民收入消费系数为β，储蓄系数为（1－β）的刚性条件下，经无限轮的商品买卖交易后，这一货币量i就又全部变为储蓄回到银行（或保存在居民自己家里）了，i/（1-β）就是货币i在消费倾向β或说储蓄倾向（1-β）下在流通过程中所能完成的商品交换的名义价值即总价格。因为从前面的分析中可知，在β过大或i过大从而产能Y不足以承受的条件下，产出Y不能满足需求y=i/（1-β），必然要引起物价上涨，从而实际的产出或收入是Y，但名义收入或完成的商品交换的名义值是 y，y＞Y。可见凯恩思定律 y=（α+i）/（1-β）不考虑产能和物价变动而得出需求决定供给的结论，顶多也只能是说明消费增加可增加名义收入，但实际收入和经济产出并不一定按此公式增长，还必须除以物价指数，即Y=（α+i）/[P（1-β）]，P 为物价指数，从而投资乘数也变为 K＝1/P（1-β）而不是K＝1/（1-β）。

同理，在加入政府和外贸部门后（g为政府支出，t为政府税收，x代表出口，m代表进口），则：

y=c+i+g+（x-m）=β（y-t）+α+i+g+（x-m）=βy+（α+i+g-βt+x-m），即：

y=（α+i+g-βt+x-m）/（1-β）也是名义收入，实际收入还要除以物价指数P。

按此思路，我们可以得到一种统计GDP的新的方法：由于每年投资和货币回流银行都在连续不断的进行之中，因此总的来说可以合理地把每年的总投资看成在当年全部通过产生的收入的（1-β）倍作为储蓄流回了银行，即当年的名义收入或名义GDP就是y=（α+i+g-βt+x-m）/（1-β），实际收入或实际GDP 是 Y=（α+i+g-βt+x-m）/[P（1-β）]。这样，只要统计出当年的总投资i（现在有）、α（用于统计GDP时可认为是政府除投资外的全部支出，包括生活救济、补贴等转移支付在内，理由从略。）、政府支出、税收、出口净值（x-m）、物价指数P（现在有）、消费倾向β（可像统计物价指数类似的方法搞个一蓝子各类代表性人群的消费倾向统计得到），就可得到当年的名义和实际GDPy和Y了，这要比直接收入法或支出法简单容易。

五、结论和建议

第一，凯恩思定律 y=（α+i）/（1-β）仅仅是方程组 y=c+i，c=（βy+α）即方程y=（βy+α）+i在数学上成立的必要条件，并非实际经济一定能产出这么多的证明或充分条件，凯恩思们把必要当成了可能，误导了世人。正确的说法应是：要满足y=（βy+α）+i，产出y必须等于（α+i）/（1-β），从而投资乘数k=△y/△i达到 1/（1-β）。y=（α+i）/（1-β）的充分条件是产能PAKaLb大于等于（α+i）/（1-β）。在产能允许的范围内，消费增加多少可使产出也增加多少；若产能充足到能保证消费系数β刚性不变，则投资增加可使产出1/（1-β）倍地增加；在产能不足时，很难保持β的刚性或会引至物价上涨，实际的投资乘数应除以物价指数P，即变成K=1/[P（1-β）]。此时是产出的多少决定着能消费多少和投资多少，并非消费得越多产出就增加越多。

第二，以需求函数y=（α+i）/（1-β）和生产函数Y＝PAKaLb导出了时间上以年为限的凯恩思定律成立的条件为β＜＝1－（α+i）/PA（K0+△K）a（L0+△L）b。消费系数和投资的最大值有确定的关系，β和i不能同时无限制地增大。投资越大或生产能力越小，β必须越小，反之可越大。

第三，在 y=（α+i）/（1-β）小于产能的情况下，增加消费可以使更多资金回到供给方，可以保证投资从而增加产出；在产能不足时增加投资可以扩张产能增加产出，从而增加可消费的绝对量，但消费系数要下降；减少投资提高消费虽可提高消费系数，但投资不能补偿资本资产的折旧损耗时生产会萎缩，从而会减少可消费的绝对量。

第四，当不限定产出期的长短时，理论上，消费系数可以无限接近于1，投资i也可以很大。但消费系数越大，达到所需产出y=（α+i）/（1-β）的时间就越长，平均年投资和产出实际是小的。

第五，把 y=（βy+α）＋i改造为yt=（βyt-1+α）＋it的想法是错误的，由此推导的无限期才逼近均衡产出的过程和时间已经不是凯恩思原来方程的意思了，也没有实际意义。

第六，为社会经济可持续地扩大再生产提供供给和需求两方面的平衡条件，正确的做法是要杜绝个人、企业、政府的浪费，国民收入应以合适的比例在资本和劳动要素之间分配，使投资和消费能相辅相成，互相促进。例如有学者对美国的长期历史资料统计结果为资本对产出的贡献约为1/3，劳动贡献占2/3左右（毛蕴诗，1988），按这个贡献比例分配收入应是较合理的。然而有资料说我国工资分配占GDP比重从1990年时的53.4%降到2005年的41.4%，现在甚至有说已降到35%的，这种不合理的分配应大力扭转，否则很难改变我国长期内需不振、消费拉动经济作用不显，只能以投资和出口拉动经济的不利局面。在保持投资增长的前提下，国民收入分配应更多地向普通劳动者倾斜以增加个人正常消费支出，使产销大体平衡。

[1]高鸿业：西方经济学（下册）[M].中国经济出版社，1996.

[2]广东省人民政府发展研究中心：广东经济蓝皮书[M].广东人民出版社，2005.

[3]毛蕴诗：公司经济学[M].东北财经大学出版社，2006.

[4]毛蕴诗：现代经济计划与分析方法[M].湖北教育出版社，1988.

[5]李善民：新编西方经济学原理[M].中山大学出版社，2003.

[6]陈国泰、朱卫平：政治经济学原理[M].广东高等教育出版社，2003.

[7]吴易风：马克思的经济增长理论模型[J].经济研究，2007（9）.