V形件自由弯曲回弹的数值模拟影响因素分析

代洪庆 ，赵妍 ，户春影 ，黄文怡

（1.黑龙江八一农垦大学工程学院，大庆 163319；2.黑龙江省农副产品加工机械化研究所）

在板料冲压成形过程中，当外力去除后，塑性变形留存下来，而弹性变形则完全消失。弯曲变形区外侧因弹性恢复而缩短，内侧因弹性恢复而伸长，产生了弯曲件的弯曲角度和弯曲半径与模具相应尺寸不一致的现象，这种现象称为弯曲件的回弹[1]。回弹在板料成形过程中，尤其是弯曲和拉深过程中影响到冲压件的尺寸精度和零件最终的形状。传统的成形工艺主要依赖以往经验，靠反复的修模、试模来解决，这不仅使生产周期大大延长、生产成本提高，更重要的是产品的质量得不到保证。

近年来随着计算机软硬件技术、板料塑性变形理论和数值计算方法的发展，开创了金属板料冲压成形数值模拟技术。其越来越受到人们的重视，通过计算机对冲压过程的仿真模拟，大大减少了试错逼近的试模环节，降低生产成本，缩短生产周期。

1 建立模型

1.1 V形件回弹角定义

V形件弯曲回弹的结果表现在弯曲角度的变化[2]。如图1所示，实线为卸载前弯曲件的形状，虚线为卸载后弯曲件的形状，卸载前弯曲中心角为α，回弹后弯曲中心角为α′，则角度变化量为

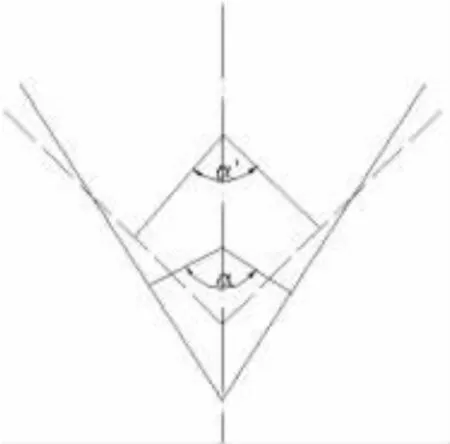
图1 回弹角定义示意图Fig.1 Angle of springback

1.2 有限元模型的建立

模拟所用的V形件的几何模型如图2所示。板料的长度为120 mm，宽度为20 mm，厚度为1 mm。板料采用08AL冷冲压钢板。板料采用36号即三参数Barlat材料模型（各向异性弹塑性材料）。36号材料模型考虑了板料的厚向异性对屈服面的影响，为了准确的预测出回弹角的大小，在网格划分单元尺寸较小，保证在90°的模具弧度上至少有4个单元，尽可能使用接近正方形的单元，为了得到精确的结果，在冲压成形回弹分析中都使用16号壳单元公式，并且壳单元厚度方向积分点数增加到7个。

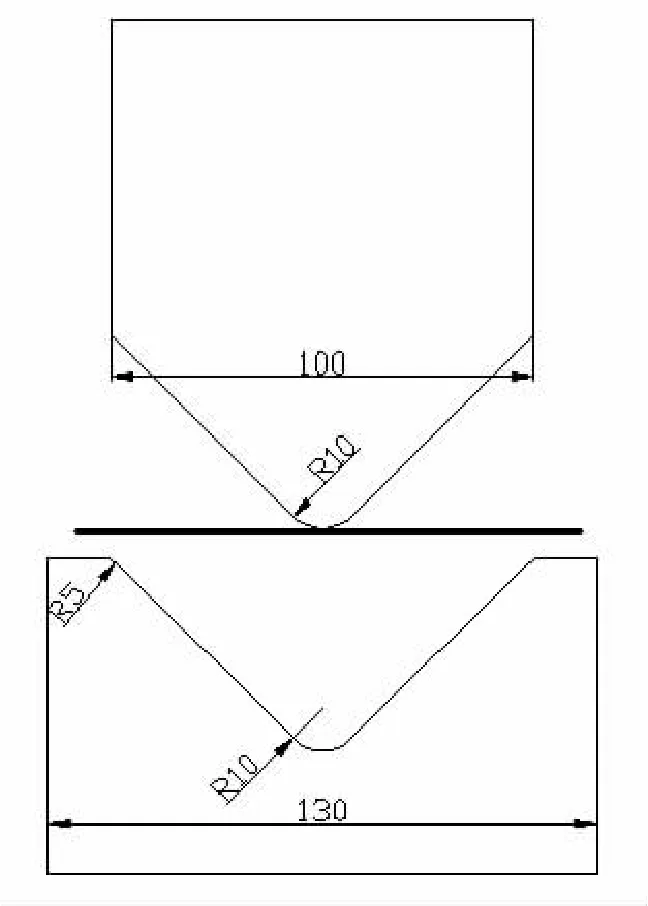
图2 V形件弯曲模具示意图Fig.2 Illustration of air V-bending

1.3 算法

回弹模拟的算法主要有两种：动力显式算法和静力隐式算法。在动力显式法的计算模型中，考虑了速度和加速度变量，模具与工件之间的接触约束条件不仅与位移有关，还应保持与两接触点间速度和加速度的协调关系[3]。动力显式算法，使得接触处理简单、实用，无需求解刚度矩阵；在发生起皱、失稳现象时不会引起数值计算困难，并且计算时间随着节点、自由度的增加仅呈线性变化，特别适合于求解大型复杂成形问题[4]。因此，动力显式算法比静力隐式算法更加接近于冲压过程的本质[5]。

卸载回弹是一个准静态过程，回弹计算是在加载过程应力分析的基础上进行的，精确计算加载应力，静力隐式算法是比较合理且相对精确的方法[6]。

本文在板料弯曲回弹数值模拟过程采用动静态联合算法。首先在UG等软件中建好三维模型并导入到LS-DYNA中，在LS-DYNA前处理中定义模具参数，划分网格，设置板料属性，并利用动态显示算法对其进行求解。在弯曲成形分析后，输出包含板料最后阶段的变形网格和应力应变数据的dyain文件，再导入dyain文件到LS-DYNA，定义约束条件，进行静态隐式回弹分析。

2 回弹的主要影响因素分析

图3为加载终了板料的等效应力分布，图4为加载终了板料的等效应力分布。从图上可以得出加载终了后应力主要集中在V形件的圆角部位，经过卸载回弹板料的等效应力明显较少。并测量卸载前后角度的变化，卸载前板料的弯曲中心角为90°，卸载后板料的弯曲中心角为92.1°，回弹角2.1°。

图3 加载终了板料的等效应力分布Fig.3 Equivalent stress distribution at the end of forming

图4 加载终了板料的等效应力分布Fig.4 Equivalent stress distribution after springback

2.1 凸、凹模圆角半径对回弹的影响

图5为板料为08AL，凸、凹模为1.1 mm，摩擦系数为 0.125，凸、凹模圆角半径分别为 5，10，15，20 mm的条件下回弹量。

这主要是因为模具的圆角小，板料的圆角部位塑性变形占变形量的比例较大，而弹性变形所占比例较小，所以凸、凹模圆角半径越小，回弹角越小。

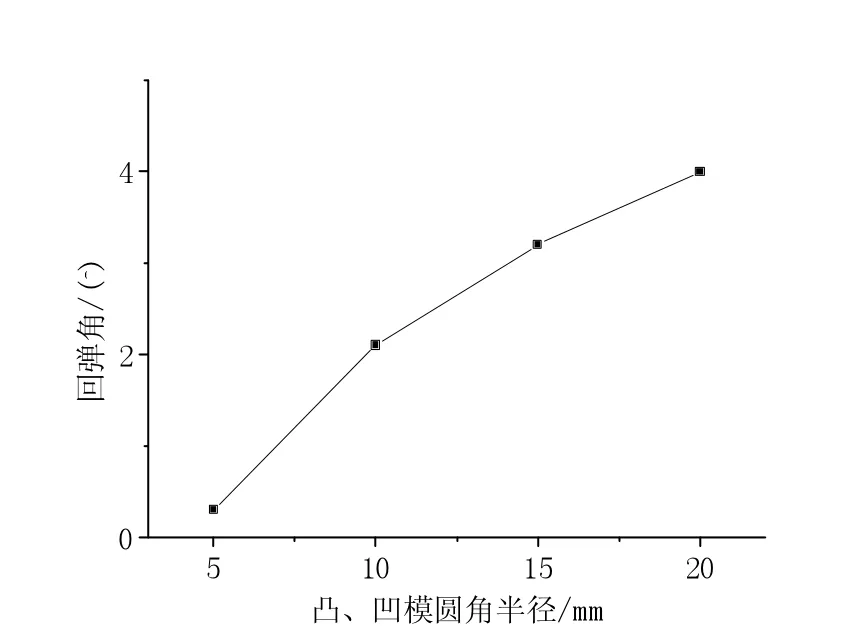
图5 凸、凹模圆角半径对回弹的影响Fig.5 Influence of punch and die radius on springback

2.2 凸、凹模间隙对回弹的影响

V型件凸、凹模的间隙主要是靠调节压力机的闭合高度来实现的，但为了保证完全的质量凸模圆角半径与凹模底部圆角半径以及凸凹模两侧，在模具闭合时完全接触或贴合。

图6为板料为08 AL，板料厚度t=1 mm，摩擦系数为0.125，凸、凹模圆角半径分别为10 mm，凸、凹模的间隙分别为1.1、1.3、1.5、2 t的条件下回弹量。

由图6可知随着凸凹模间隙增大，回弹角增大。这是因为间隙大，材料处于松动状态，弹性回弹较大；间隙小，材料被挤压，塑性变形较大，回弹就小。

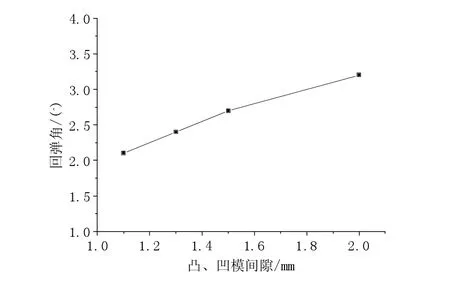
图6 凸、凹模间隙对回弹的影响Fig.6 Influence of die clearance on springback

2.3 材料性能对回弹的影响

图7为板料分别为08AL、高强度钢、铝合金3种不同力学性能的材料，其力学性能如表1所示。凸、凹模为1.1 mm，摩擦系数为125，凸、凹模圆角半径分别为10 mm的条件下回弹量。图中横坐标1，2，3分别代表08AL，高强度钢HLSA300，铝合金AA6010。由图7可知铝合金的回弹角比高强度钢大，高强度钢的回弹角比08AL大。其主要原因是材料屈服极限σs弹性模量E越小，则弯曲后回弹角越大。

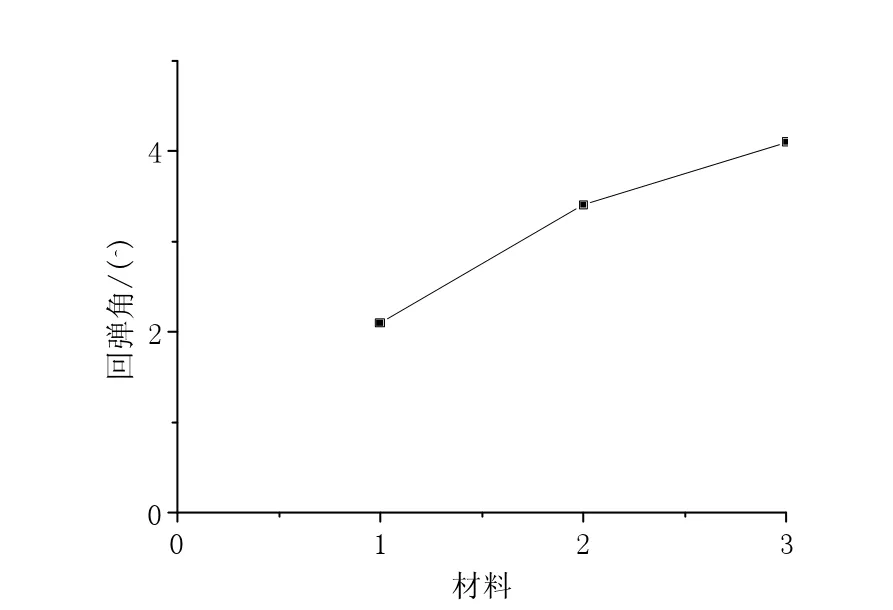
图7 材料力学性能对回弹的影响Fig.7 Influence of material properties on springback

2.4 摩擦系数对回弹的影响

图8为08AL，凸、凹模为1.1 mm，凸、凹模圆角半径分别为10mm，摩擦系数分别为0.10，0.125，0.15，0.20 的条件下回弹量。

由图8可知，但由于增大摩擦系数可以塑性变形量增大，回弹角减小，但摩擦系数对回弹角的影响较小。

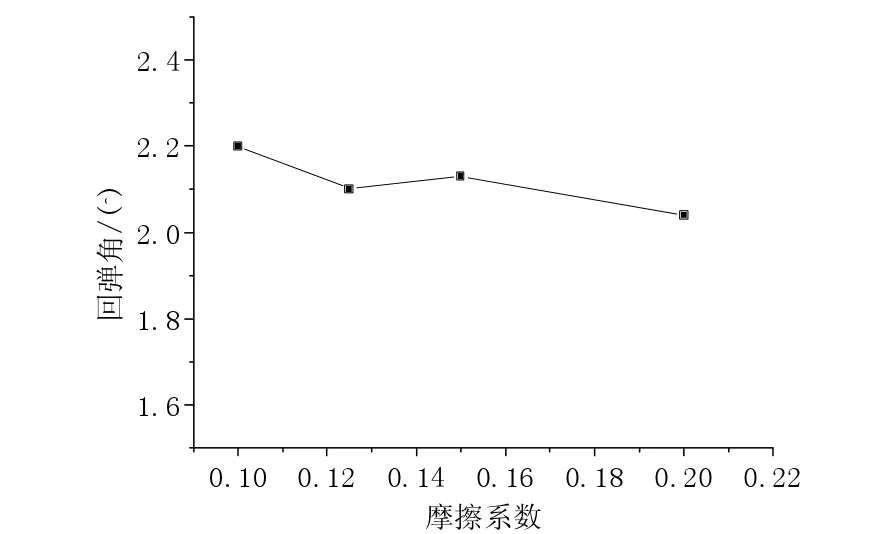
图8 摩擦系数对回弹的影响Fig.8 Influence of Friction coefficient on springback

表1 材料性能参数Table 1 Material properties of sheet metals

3 结论

通过对V形件弯曲回弹过程的模拟可以得出以下结论：

3.1 影响V形件回弹的因素中凸、凹圆角半径，凸、凹模间隙，板料的力学性能参数对弯曲回弹角影响较大，而摩擦系数影响较小。

3.2 通过利用LS-DYNA动静态联合算法的求解功能对V形件弯曲成形和回弹进行模拟，大大减少了试错逼近的试模环节，降低生产成本，为模具修正提供了有力依据。

［1］焦明华，于军涛，解挺，等.板料冲压成形回弹模拟的评述［J］.锻压技术，2007，32（6）：1-5.

［2］肖景容，姜奎华.冲压工艺学［M］.北京：机械工业出版社，1994.

［3］Krasovskyy Andriy，Schmitt Winfried，Riedel Hermann.Materialcharracterizations forreliable and efficient springback prediction in sheet metal forming ［J］.SteelResearchInternational，2006，77（9-10）：747-753.

［4］孙希延，施浒立，纪元法.板料拉深成形数值模拟关键算法的比较［J］.锻压技术，2006，（2）：19-22.

［5］刘红山，李慎国，谢世坤.动力显式算法在汽车覆盖件成形过程有限元模拟中的应用［J］.南昌大学学报，2004，（4）：4-8.

［6］Sun P.Control system of a mini hydraulic press for evaluating springback in sheet metal forming［J］.Journal of Materials Processing Technology，2006，176（1-3）：55-56.