一种自适应的雾天降质图像清晰化方法研究

吴振宇， 姚洪利， 杜少军

(1.国防科技大学光电科学与工程学院，长沙 410073;2.空军装备研究院雷达所，北京 100085)

0 引言

有雾天气条件下，光在大气介质中传播时会受到悬浮大气颗粒散射、折射等复杂作用而发生变化，导致户外监视系统获取的景物图像对比度下降、颜色退化，甚至改变，严重影响了监视系统效能的发挥。因此，对恶劣天气条件下(雾、雨、烟、雪)的景物图像进行清晰化处理具有重要意义。Oakley等人［1］基于Mie散射定律，构造了一个多参数的退化模型，并通过统计模型估计退化模型参数，但只适用于灰度图像。Tan等人［2］进一步结合图像对比度降质与波长关系，将上述模型扩展到彩色场景。Oakley在此基础上又构建了一个动态video去天气系统，但其需要价格昂贵的雷达或距离传感器等硬件设备获取精确的场景深度信息。Nayar等人［3］简化大气传播原理，总结出两个主要传输模型，基于该模型，Narasimhan［4］通过两幅不同天气条件下的有雾图像计算场景深度以及大气散射系数，从而实现清晰化，但是由于场景景物的不稳定，很难获取到同一场景的两幅或多幅不同天气条件下的图像。国内祝培等人［5］采用局部直方图均衡化方法去除雾的影响。本文从图像增强的角度出发，吸取了 Retinex［6］理论优势，把雾对景物影响等效成光照条件的变化，并将直方图幂次变换函数均衡化与其相结合，既克服了Retinex理论对浓雾天气降质图像增强的失真，又补充了局部直方图均衡化去雾在图像颜色细节上的损失。而且该方法不基于物理模型，不需要场景深度、大气散射系数等很难精确得到的天气条件参数，因此也就降低了对硬件设备的要求。

1 Retinex理论及其改进的求解算法

1.1 Retinex 理论基础

Retinex理论最早由Maxwell提出，后由Land研究得到。Retinex理论认为，图像的形成取决于环境的照明和物体表面对照射光的反射，其表达式为

式中:L为入射光(即光照图像，决定S的动态范围);R为反射图像，表示物体的反射特性;S为人眼或监视系统获取的图像。Retinex理论的目的就是从观测图像S中获取物体的反射性质R，得到物体的本来面目。本文将雾对景物图像的影响等效成光照的变化，由已知的降质图像S和光照图像L求出反射图像R，即为要求的去雾图像。

1.2 改进的Kimmel变分模型

为将式(1)的乘积关系转换为更为易求的求和关系，可以做对数变换，即:

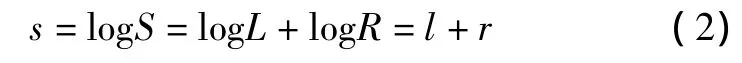
Kimmel［7］提出的变分模型也同样在对数域中处理，其数学表达式为

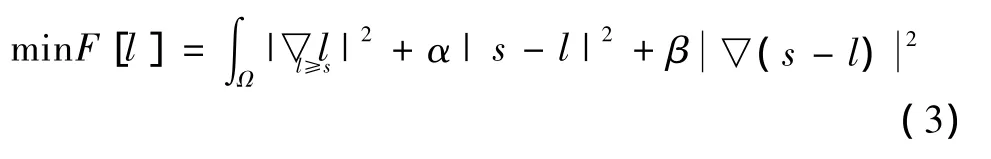
式中:Ω表示图像空间;α，β为代价因子;限制条件l≥s是因为光照图像强度高于观测图像强度。称作保真项，防止光照图像l收敛为常数是保证反射图像连续的正则项。分析Kimmel变分模型不难看出，只要解出使得代价函数F［l］取得最小值时的l，代入到式(2)即可求出反射图像。为了使式(3)达到最小值，其等式右侧3项都要趋向于最小，这样就使得l和s－l(即反射图像)要更加平滑，而l和s则要更加相关。但是光照图像强度变化比较剧烈时，这种光照图像的全局平滑会使得在强度变化边界产生严重的模糊，形成光晕伪影。而且模型中第3项在保证平滑性时是以牺牲颜色细节为代价的。为了更好地保护图像细节信息，可以在式(3)的代价函数上增加一项增强图像细节信息的式子λ▽2(l－s)▽2s，其中λ为控制因子，通过控制它的大小可以调节反射图像中细节的表现程度。修改后的变分模型即为

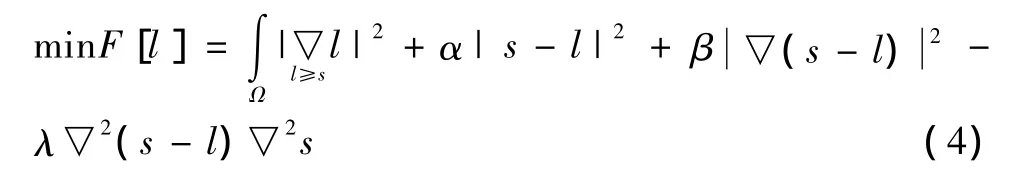
为使式(4)取最小值则新增加的项中▽2(s－l)和▽2s要保证同号，且▽2(s－l)的幅值要尽可能大。而▽2=Δ为拉普拉斯算子，实际上就是对图像做无方向性的微分，这种变换使图像边沿增强，因此▽2(s－l)幅值的增大即是保护了反射图像细节信息。

1.3 求解变分模型的四邻域算法与金字塔分层

首先对修改后的Kimmel变分模型做离散化处理，其中的梯度运算转换为差分运算，新增加的项λ▽2×(l－s)▽2s，本文采用拉普拉斯算子的四邻域掩模代替二阶微分。则离散化后的代价函数可以近似的表示为

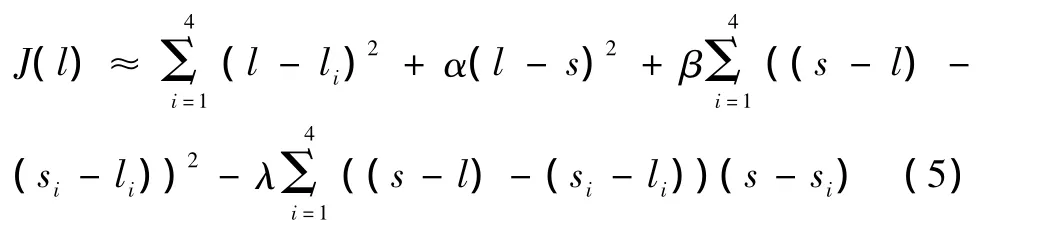
很明显，当式(5)对l的导数等于零时，取得最小，而此时的l也就是要求的光照图像中的最佳像素值。经过简单的数学推导，可得:

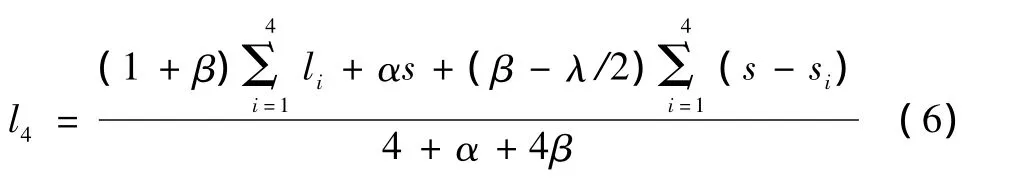
式(6)中的系数λ/2可以规整化为λ，对结果没有影响。但是在求解此代价函数时，要求图像中每个像素的四邻域像素值保持不变，即每个像素的最佳值的获取要依赖其周围四邻域内的像素，如此像素之间既相互依赖又相互干扰，很难判断最终结果的取值。故此，可以将离散图像分成2*2的基本单元区域，沿其对角线方向将像素划分为两个类别:A类和B类。如图1所示。在求解时，先固定其中一类，求解另一类的最佳值，然后再将此过程反之进行，如此交替迭代，则可得到不断精确的光照图像。

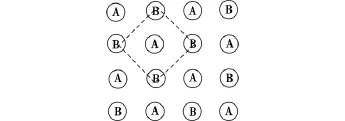
图1 四邻域的划分Fig.1 Division of 4-neighborhood

2 直方图幂次变换函数均衡化

Retinex理论虽然在恢复景物本来特性上有明显的优势，但是对于处理雾化降质图像时，经常把雾和场景物体混同，所以有时去雾后的图像白色偏重，影响了复原后图像的清晰度。故此，本文引入直方图均衡化图像增强法思想。

传统的直方图均衡化法［8］，其变换函数为累积积分函数，离散的映射关系如下:0≤rk≤1，T为变换函数，rk为第 k级灰度，p(rk)为 rk灰度的概率。这种变换简单易算，但是其变换结果不可调节，体现在输出图像上就是亮度不可调，对于较暗或较亮的图像增强后很多细节无法清晰表现。为此，可以把变换函数修改为幂次函数:y=αxγ，0≤x≤1，0≤α≤255，α为范围系数，一般取255。xγ的形式满足值域属于［0，1］区间，且在此区间上单调递增。当α=255，γ=1时即为累积积分变换函数。当γ＞1时，适用于过亮图像，当γ＜1时，适用于过暗图像，其原理如图2所示。

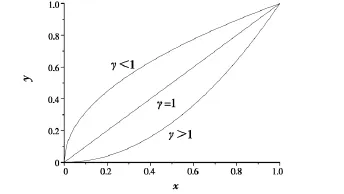
图2 幂次变换函数示意图Fig.2 Sketch map for power transformation function

由于部分子块重叠［9］和局部直方图均衡化计算量过大，且有时出现过亮、过暗情况，故本文只在全局范围内做直方图均衡。

3 直方图幂次变换均衡法与Retinex理论的结合原则

将两种算法结合，存在先后的问题。基于Retinex理论的增强算法在恢复景物本来特性上表现优秀，而直方图幂次变换均衡法则更适合提高图像的对比度。如果输入图像在颜色上有失真，先做均衡增强则会加剧颜色的异常，增加Retinex理论增强法恢复图像原本模样的难度，冲击其恢复的效果。经过大量的实验发现，将直方图幂次变换均衡法运用在Retinex增强之后效果最佳。但是通过实验还发现，并不是所有经过Retinex增强后的图像还需要第二次直方图均衡增强，为此引入了方差指标作为判据。因为方差可以体现一幅图像的对比度大小。通过计算第一次增强后图像的方差，并将其与输入图像的方差指标相比较，如果小于该指标则结合直方图幂次均衡化算法，否则直接输出图像。

4 算法流程

1)计算输入图像方差指标σ0，对输入图像做对数变换，初始化参数值。取 α =0.008，β =0.1，λ =0.3。金字塔分解层数nlayer=n，每层的四邻域迭代次数niter，线性拉伸系数δ。

2)将输入图像与高斯低通滤波器做卷积，逐次做抽样率2∶1的下采样得到金字塔序列图像si(1≤i≤nlayer);初始化 ln，0=max(sn)。

3)计算顶层sn的光照图像ln。在顶层图像上做式(6)的四邻域迭代。则ln=l4(ln，niter)。

4)if n=1，则ln为最终光照图像估计值。else利用双线性插值做上采样得到下一层光照图像初始值ln－1，0，令 n=n －1，跳至步骤 3)。

5)把得到的最终光照图像l1代入式(2)，得到反射图像 r。计算其方差 σ2，if σ≤3/5σ0，将 r代入步骤6)。else直接输出。

6)直方图幂次变换函数均衡化。通过控制γ值的大小，调节输出图像亮度，直至清晰化效果最佳。本文γ取0.8。本文处理彩色图像在RGB空间内分别进行，最后再将3个通道结果合成。

5 仿真结果

算法的应用效果如下所示。图3为雾天户外监视系统捕获的原始图像。图4为单一运用Retinex理论增强法清晰化的结果图。图5为将直方图幂次变换均衡化应用在Retinex理论增强法之前所得效果图，图6为本文提出算法清晰化结果图。从4幅图中可以看出，单一运用Retinex理论增强法处理，虽然在一定程度上恢复了场景景物原貌，但是道路两侧的小树还是被雾气遮挡。而将均衡法用在Retinex理论增强法之前，则导致了天空颜色的异变，上文中已经分析，这是由于均衡化增强了颜色失真所致。而将均衡化法运用在Retinex理论之后，对整幅图像质量的提高是非常明显的。道路的颜色更加接近实际，路边的小树枝干更加清晰，远处的路灯也能较容易地分辨出来，甚至在十字路口道路左侧的一座小房子也能比较容易见到。图7为将幂次变换的γ值设定为2的结果图，可以明显看到图像整体变暗。说明该方法对亮度的调节是非常得力的。

图3 原始图像Fig.3 The original image

图4 单一运用Retinex理论增强法结果图像Fig.4 The result when only using Retinex enhancement

图5 直方图幂次均衡化法用在Retinex理论增强法之前结果图像Fig.5 The result when using power transformation HE before Retinex enhancement

图6 直方图幂次均衡化法用在Retinex理论增强法之后结果图像Fig.6 The result when using power transformation HE after Retinex enhancement

图7 γ=2时的结果图像Fig.7 The result for γ =2

6 小结

本文吸收了Retinex理论保持色彩恒常的理论优势，对典型的Kimmel变分模型做了修改，增加了一项保持细节信息的因式，进一步提高了图像颜色的逼真度。引入了直方图均衡化思想，将传统的累积积分变换函数修改为幂次变换函数，使输出亮度可调。最后将两种方法相结合，讨论了结合原则，把图像方差作为结合与否的判据。实验表明，该方法对清晰化雾天降质图像有很好的效果。由于采用了四邻域迭代和金字塔分层的求解方式，算法的工作量较低，效率较高。

［1］OAKLEY J P，SATHERLEY B L.Improving image quality in poor visibility conditions using a physical model for degradation［J］.IEEE Trans Image Processing(S1057-7149)，1998，7(2):167-179.

［2］TAN K，OAKLEY J P.Physics based approach to color image enhancement in poor visibility conditions［J］.Optical Soc Am A，2001，18(10):2460-2467.

［3］NAYAR S K，NARASIMHAN S G.Vision in bad weather［C］//Proc Seventh Int’l Conf Computer Vision，1999，2:820-827.

［4］NARASIMHAN S G，NAYAR S K.Removing weather effects from monochrome images［C］//Proc IEEE Conf Computer vision and Pattern Recognition，2001(2):186-193.

［5］祝培，朱虹，钱学明，等.一种有雾天气图象景物影像的清晰化方法［J］.中国图像图形学报，2004，9(1):124-128.

［6］RAHMAN Zi-ur，JOBSON D J，WOODELL G A.Retinex processing for automatic image enhancement［J］.Journal of Electronic Imaging，2004，13(1):100-110.

［7］KIMMEL R，ELAD M，SHAKED D，et al.A variational framework for Retinex［J］.International Journal of Computer Vision，2003，52(1):7-23.

［8］GONZALEZ R C，WOODS R E.Digital image processing［M］.2 版.北京:电子工业出版社，2003.

［9］翟艺书，柳晓鸣，涂雅瑗，等.一种改进的雾天降质图像的清晰化算法［J］.大连海事大学学报，2007，33(3):363-366.