基于改进型模糊层次法的维修性综合评估研究
2010-07-03刘福成尚朝轩
刘福成,尚朝轩
(军械工程学院,河北 石家庄 050003)
1 引言
随着高新技术的发展,现代装备不仅要求高可靠性,而且要求良好的维修性。装备使用维修性是考察装备战备完好性的一个基本要素。这是因为,使用维修性是在装备的实际使用维修中表现出来的维修性,它不但包括因装备设计和制造所决定的固有维修性,而且包括装备使用操作人员的技术水平、所能提供的维修保障条件、维修策略等各种因素的综合影响,更能直接地反映装备的作战使用要求。维修性评估指标既有定性的,也有定量的,以往典型的评估方法多是针对某个定量指标的,但是在实际使用中往往需要对装备的维修性进行综合评估,需要考虑各种因素,以便对装备的维修性进行全面的了解和掌握,所以掌握装备的使用维修性能够更好地为部队服务。因此,本文鉴于评估指标中既含有定性指标,也含有定量指标,采取改进AHP法来确定评估指标权重,应用模糊方法对维修性进行综合评估。
2 模糊综合评估数学模型
模糊理论是在1965年由L.A.Zadeh首先提出来的。模糊层次综合评价法是将模糊数学和层次分析法相结合的一种分析评价方法,比较好地解决了复杂系统多目标综合评价问题,是当前比较先进的评价方法。
对某一事物进行评价,若评价的指标因素有n个,分别表示为u1,u2,u3…un,则这n个评价因素便构成一个评价因素的有限集合U={u1,u2,u3…un}。若根据实际需要将评语划分为m个等级分别表示为v1,v2,v3…vm,则又构成一个评语的有限集合 V={v1,v2,v3…vm}。
模糊层次综合评估模型建立的步骤如下:
a)确定评判因素集U(论域)
根据目的与要求给出合适的评判因素并将评判因素分类,即:
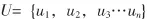
式中: ui={ui1,ui2,ui3…uij},i=1,2…n。
b)确定评语集V(论域)
应尽可能地包含事物评论的各个方面,即:
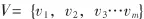
c)确定权重集
在评判的过程中,不同的因素其重要程度是不同的,因此权重的分配是十分重要的。
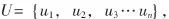
d)确定单因素模糊子集
对每一个因素ui分别对其在评语集V的各方面进行单因素评判,形成单因素评价模糊子集。
e)建立评价矩阵R
依据U中的评判因素,根据前面已经确定的单因素模糊子集,多种因素的评价模糊子集可构成一个评价矩阵R。

f)做模糊综合评估
模糊综合评估数学模型为:
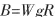
对于因素众多的情况,可以采取多层次的模型,一般采取两层次模型。
3 维修性及其评估指标
维修性是产品的一种质量属性。维修性有其严格的定义:产品在规定的条件下和规定的时间内,由规定的人员,按照规定的程序和方法进行维修时,保持或恢复其规定状态的能力。从其定义中可以看出,装备的维修性不仅取决于装备的设计和制造因素,而且还受规定的人员、程序和方法等装备之外的诸多因素的约束,影响维修性指标的具体因素可以参考相关文献,这里不再详细叙述。
维修性评估指标可以分为定性指标和定量指标。定性指标的评估内容主要有维修的可达性、检测诊断的方便性与快速性、零部件的标准化与互换性、防差错措施、工作场地的维修安全性、人素工程要求等。定量评估是对装备的维修性指标进行评估,定量指标的评估内容主要有平均维修时间、最大修复时间和重构时间参数等。
对某装备的维修性综合评估,结合部队维修的实际情况和战时环境的特殊要求,立足于现有的维修资源,对评估指标综合考虑各种因素,对评估总目标进行多层次分解,如图1所示。
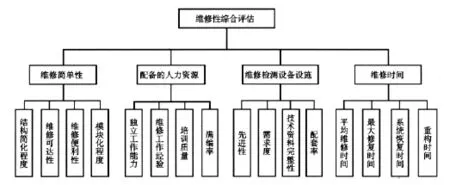
图1 维修性综合评估影响因素指标体系
4 模糊层次综合评判在维修性评估中的应用
4.1 确定维修性综合评估的因素集
根据前面的分析,维修性评估指标因素集分为一级指标集和二级指标集,见上图1。
4.2 确定评语集
根据以往的经验和现实需求确定评语集为5个等级,即:
V={v1,v2,v3…vm}={好,较好,一般,较差,差}
4.3 确定权重集
权重分配多是运用传统的层次分析法,层次分析中的判断矩阵元素是精确数,但是,因为专家评判时人的主观因素以及事物的复杂性用精确的数来描述重要性是很困难的,传统的层次分析法过于刚性,因此用改进的层次分析法来确定各个因素的分配权重,改进型层次分析法原理参考文献 [5-6]。结合图1所建立的评估指标层次结构,使用成对比较和专家咨询法来构造判断矩阵,其表示的是与上层某一元素相关的本层元素之间的相对重要性关系,标度值由Saaty的1~9值法决定。下面以计算第二层相对于第一层的权重为例,表1为第二层相对于第一层的判断矩阵。
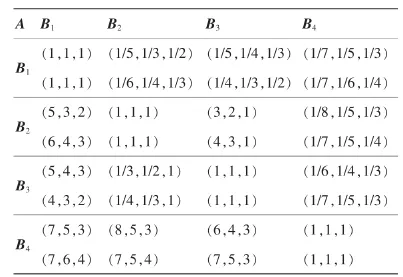
表1 第二层相对于第一层的判断矩阵
经过计算得到精确的判断矩阵为:
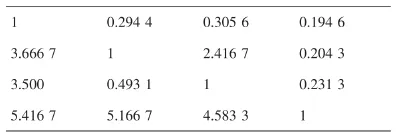
1 0.294 4 0.305 6 0.194 6 3.666 7 1 2.416 7 0.204 3 3.500 0.493 1 1 0.231 3 5.416 7 5.166 7 4.583 3 1
转换为精确的判断矩阵以后,利用层次分析法计算得到权重分配为:
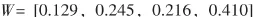
经计算 λmax=4.247 8,CI=0.052 6,RI=0.89,可见判断矩阵具有满意的一致性,可以采纳。
用同样的方法确定第三层相对于第二层的权重集为:

4.4 确定单因素模糊集及评估矩阵
维修性评估指标既有定量指标又有定性指标,因此其评估方法有所不同。对于无量纲成比率形式的定量指标可以采取隶属度函数法,而对于那些具有不同性质和度量标准的定量指标和定性指标可以采取专家打分法,运用模糊隶属函数。按照指标的特点和相关实践经验采用常见的模糊分布——岭形分布,分为偏大型、中间型和最小型隶属函数。评语集中 “好” 属于偏大型,“较好” “一般” “较差”属于中间型,“差”属于最小型,其函数式分别为:
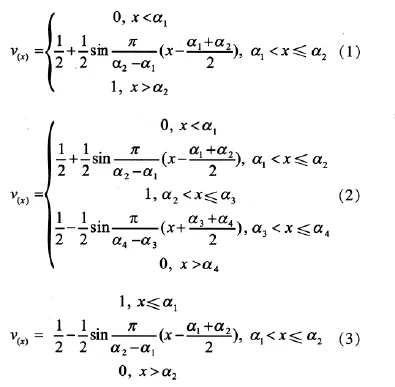
其中,式(1)相应的参数为 α1=0.85,α2=0.95; 式(2)中 “较好” “一般” “较差” 的相应参数分别为: α1=0.65,α2=0.75,α3=0.85,α4=0.95; α1=0.45,α2=0.55,α3=0.65,α4=0.75; α1=0.35,α2=0.45,α3=0.55,α4=0.65; 式(3)中的相应参数为 α1=0.25,α2=35。
将专家评分处理结果的数据带入到隶属函数,就可以得到各个单因素模糊集,最后可以得到模糊评估矩阵。例如:简单维修性的模糊评估矩阵为:
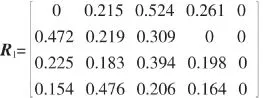
模糊评估矩阵中的每一行是单因素的模糊集。
4.5 对某装备进行维修性综合评估
应用前面介绍的评估模型以及求得的相应权重和模糊评估矩阵,可以求得第二层单因素的模糊集,分别为:
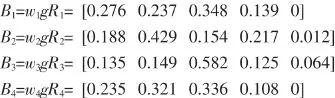
通过转换,可以求得目标的综合评估结果为:
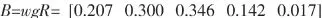
根据综合评估最大隶属度原则,该装备的维修性综合性能结果为一般。
5 结束语
本文应用模糊综合评估方法来解决某装备的维修性综合评估问题。在评判过程中,综合考虑了多种因素的影响,从指标的模糊化处理到各指标权重的确定,都充分考虑到各领域专家的定性分析,通过将其量化并进行科学的计算,最终得出了合理的评判结果,可以合理且全面地评估使用装备的维修性能,指导部队更好地开展装备维修工作。
[1]甘茂治,吴真真.维修性设计与验证 [M].北京:国防工业出版社,1995.
[2]GJB 2072-1994,维修性试验与评定 [S].
[3]袁嘉祖.灰色系统理论及其应用 [M].北京:科学出版社,2002.
[4]李安贵,张志宏,孟艳,等.模糊数学及其应用 [M].北京:冶金工业出版社,2000.
[5]樊为刚,侯丽红.层次分析法的改进 [J].科技情报开发与经济,2005,15:153-154.
[6]王莲芬,许树柏.层次分析法引论 [M].北京:中国人民大学出版社,1990.
[7]刘普寅.模糊理论及其应用 [M].长沙:国防科技大学出版社,1998.
