水电机组集成监测系统中铁心振动分析

万 元，李朝晖，薛 松

（华中科技大学水电与数字化工程学院，武汉 430074）

引言

国内外水电站的运行经验表明，定子铁心的磁振动是水轮发电机发生事故和严重损坏的根源之一[4]。因此，有必要对定子铁心振动进行在线监测，实时了解铁心振动的大小以及信号特征，以便于更合理地处理发电机运行过程中出现的问题。

水轮发电机定子铁心振动包括转频振动和极频振动[1]，其中极频振动中频率为 100Hz振动可能与定子铁心的固有频率非常接近，因此是在线监测的重点。铁心振动与机组定子电流、励磁电流、定子温度等机组的运行参数关联度比较大[7]。因此，在分析定子铁心振动时，必须结合机组的运行参数，这样才能保证监测结果的高可靠性。

本文利用最优维护信息系统（HOMIS）[13,14]提供的水电机组集成监测环境，研究了定子铁心振动的分析方法：在有效采集铁心振动信息、计算振动指标数据的基础上，结合机组的运行状态，分析铁心振动特征及状况，最终实现铁心的故障诊断。

1 水轮发电机定子铁心振动特征

水轮发电机的定子铁心振动分为转频振动和极频振动[1]。

1.1 转频振动

定子内腔和转子外圆之间气隙不均匀，而在定子和转子之间产生不平衡的电磁拉力，是大直径水轮发电机组的主要振源之一[1,3]。当定转子气隙不均匀时，大轴每转一周，定子和转子之间有一次最小间隙相遇，若正常间隙为δ，最小间隙为α，则气隙偏差值e=δ−α。在最小间隙处定子、转子间产生的不均衡磁拉力，可近似地用公式（1）表示[1]：

式中：L、D分别表示转子高度和直径（单位：cm）；B表示磁通密度（单位：Gs）。β为无量纲系数，与发电机类型、磁场分布和绕组结构等有关，一般β = 0.2～0.5。因此，定子铁心转频振动的频率与水轮发电机组运行转速n之间的关系可由（2）表示。

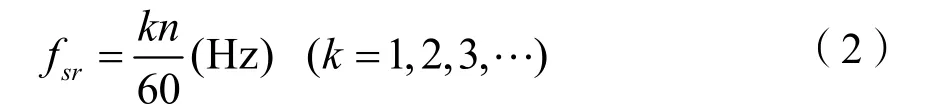
式中：fsr为转频振动的频率；n为机组转速。转频振动特征是振动频率为机组转频的整数倍，随气隙的磁通密度B的增大而加剧。

1.2 极频振动

水轮发电机的极频振动主要由定子分数槽绕组引起[1,5,9,10]。分数槽绕组将导致分数次谐波磁场的存在，引起的铁心极频振动，基本上分为四种情况：

（1）分数次谐波磁场与基波磁场联合产生的振动；

（2）两个分数次谐波磁场共同引起的振动；

（3）单个分数次谐波磁场引起的振动；

（4）分数次谐波与高次谐波磁场共同作用产生的振动。

如果定子电流的频率为50Hz，则可得（1）、（2）、（3）引起的极频振动为100Hz。第四类振动的频率为100Hz、200Hz、……。根据力学分析可知[1,9,10]，冷态下铁心振动的幅值由振动力波的大小、力波的空间节点次数、力波的频率及铁心的固有频率共同决定。因此，对于常规设计的定子绕组，由于次谐波磁场幅值和高次谐波磁场幅值的幅值很小，它们单独或者联合产生的振动对定子威胁不大，最有可能引起铁心剧烈振动的是基波磁场和那些与基波磁场极对数相差小、旋转方向相反的次谐波磁场的联合作用。从而可得出极频振动具有以下特征：

• 振动主频为100Hz；

• 设f为定子电流频率，极频振动频率fsp满足（3）；

• 振动强度与磁场幅值密切相关。

文献[1]经计算得出，铁心的固有振动频率可能出现在100Hz附近，为防止共振，100Hz下的振动幅值是在线监测的重点。

2 铁心振动与机组运行状态的关系

2.1 机组运行状态与铁心振动力波的关系

定子回路的磁动势F(x,t)可由（4）计算[4]。

式中：W为每相串联匝数，kwn为n次谐波的绕组系数(n为正转磁场时取正，否则为负)，kwn计算可参见文献[9]、[10]，其取决于电机定子绕组结构；τ1为二级波的极距。I为定子电流（电枢电流）。当不计磁场饱和，且不考虑转子高次谐波磁势，由水轮发电机运行矢量图知[6]，转子基波磁势f(x,t)可由(5)表示。

式中：N为励磁绕组匝数；Kf为常数，即基波对应傅立叶系数；If为励磁电流，ψ为发电机内功角，p为定子基波极对数。假设空间气隙均匀，即气隙磁导Λ为一常数，当气隙磁导为µ0时，定转子产生的振动力波q(x,t)由（6）计算。

设 qsr(x,t)表定子和转子磁场共同作用产生的力波；qss(x,t)表定子磁场单独产生的力波；qrr(x,t)为转子磁场单独产生的力波，则q(x,t)=qsr(x,t)+ qss(x,t)+ qrr(x,t)。结合（4）、（5）、（6）分析可得（7）。

因此，振动的驱动力波由定子电流和转子电流共同决定。在不考虑在机组不同状况时定子铁心与定子机座的耦联程度差异，仅从定子受力考虑，可得出以下几点结论。

（1）当发电机空载时，I=0，空间气隙磁场由 If引起，随着If增大，振动力波将随之增大。

（2）发电机带负荷运行时，由水轮发电机运行矢量图[6]得定子电流I、励磁电流If、有功P要遵从一定的协联关系，可得以下几点：

• If不变时，I的增大能引起振动力波加大；

• I不变时，If的增大能引起振动力波加大；

• 当P恒定时，由于I和If的数值结构不同，振动力波将存在差异；

“怀旧”，一方面是两岸听众的审美特征，而另一方面也反映出当代华语流行乐坛存在的问题。如当前各个经纪公司在筹划歌手个人演唱会时，都在打“怀旧”牌，列出该歌手多年来唱过的经典曲目以增加演唱会的市场号召力，让歌迷到现场“见证青春岁月”。[29]这一方面证明了这些流行歌手的影响力，另一个方面也显示了整个流行乐坛一定程度上的青黄不接。[29]

• 相对于空载，发电机负载运行时，由于定子电流的出现以及励磁电流的增大，振动力波显著增大。

（3）发电机工况变化瞬间，由于水力及其他动力的冲击，发电机的大轴的振动相对剧烈，定转子气隙畸变（偏心严重等），导致不平衡拉力加大，定子铁心的转频振动将增大[1,9,10]。

2.2 定子温度对铁心振动的影响

在发电机运行过程中，定子铁心的温升一般高于定子机座的温升。当定子铁心温度升高时，由于固体的热胀冷缩特性，定子铁心受热膨胀时，与定位筋间的间隙逐渐减少，使定位筋的受力越来越大，从而定子机座与铁心的耦联程度逐渐变高，当温度升高到一定程度时，最终导致机组和铁心联合成一个整体振动。因此，在同样的振动力波作用下，定子温度将导致铁心振动的剧烈程度不一致，温度越高，振动越小。

因此，铁心振动与机组运行状态存在较为密切的关系，脱离机组运行状态来分析定子铁心振动特征，将容易造成铁心“共振”现象的误判，无法得出全面、正确的结论。

3 发电机集成监测环境下铁心振动分析

为实时了解定子铁心振动的状态特征，分析机组不同运行状况下定子铁心振动的特征，实现定子铁心“共振”故障的有效诊断，设计了水轮发电机集成监测环境下的定子铁心振动分析方法，其框架如图1所示，具体包括信号获取、指标计算、集成分析与故障诊断四个方面。

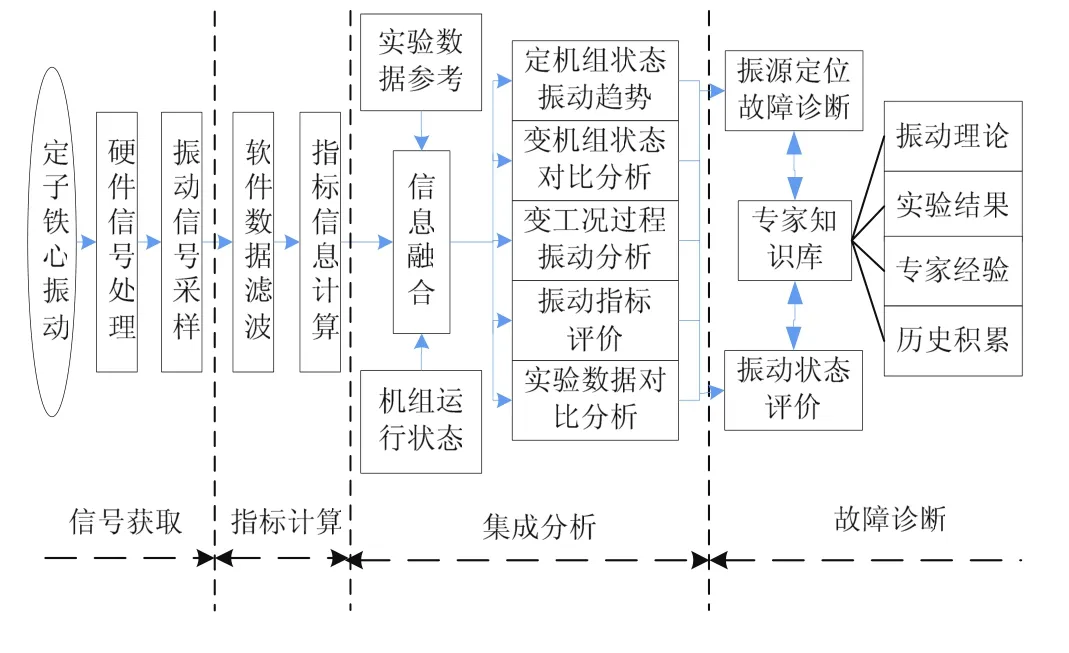
图1 集成监测系统中铁心振动分析方法

3.1 信号获取

信号的获取指数字测量装置使用传感器技术、硬件信号调理技术、采样技术等获得反映定子振动状态的原始信息。信号获取是定子振动集成监测与分析的物理基础，其中传感器实现振动信号由非电量到电量的转化，信号采样则实现模拟量到数字量的变换。

3.2 指标计算

指标计算利用原始振动数据计算出反映发电机定子铁心振动状态、能够体现振动本质特征的信息。因此，指标计算直接关系到在线监测结果的可靠性。

现场信号存在干扰，为保证指标计算的真实性，在振动指标计算前必须抑制干扰。本文使用时域计算、傅立叶变换、小波变换等手段计算定子铁心振动在时域及频域的指标信息，设机组的转频 fr，定子电流频率为f，铁心振动的指标信息的详细内容见表1。

表1 铁心振动的指标信息

3.3 集成分析

（1）定机组状态振动趋势，计算机组运行状况相同下（即定子电流、励磁电流、温度一定时）铁心振动的随时间的发展趋势，评价定子铁心的性能，诊断“共振”现象是否发生。

（2）变机组状态振动对比，对比机组运行状态不同时的铁心振动的状况，总结铁心振动随机组运行状态的变化规律。

（3）变工况过程振动分析，分析机组在变工况的瞬态过程中，铁心振动的特征。对比不同的变工况瞬态过程中，铁心振动特征的差异。

（4）振动指标评价，实时评价振动指标信息的数值，分析定子振动的剧烈程度。

（5）实验数据对比分析，对比分析发电机铁心振动与数字化后的实验数据，评价定子振动偏离实验状态的程度。

3.4 故障诊断

在铁心振动专家知识库的基础上，根据集成分析的结果，实现铁心状态评估和故障诊断。专家知识库的知识由振动理论、实验结果、专家经验及历史积累综合构成，同时也在实时在线监测的过程中不断补充。在结合数字化的专家知识[13]及历史数据的基础上，本文采用三步完成故障诊断：（1）阈值法则判断定子铁心的故障是否存在；（2）模糊理论评价故障的严重程度；（3）逻辑推理获取定子铁心故障的原因，并给出维护建议。

4 定子铁心振动在线监测系统

根据以上设计的机组集成监测环境下定子铁心分析方法，本文利用葛洲坝水力发电厂最优维护信息系统（HOMIS）[13,14]提供的机组集成监测环境下，实现了发电机定子铁心振动的在线监测与分析。HOMIS的结构如图2所示[13,14]。

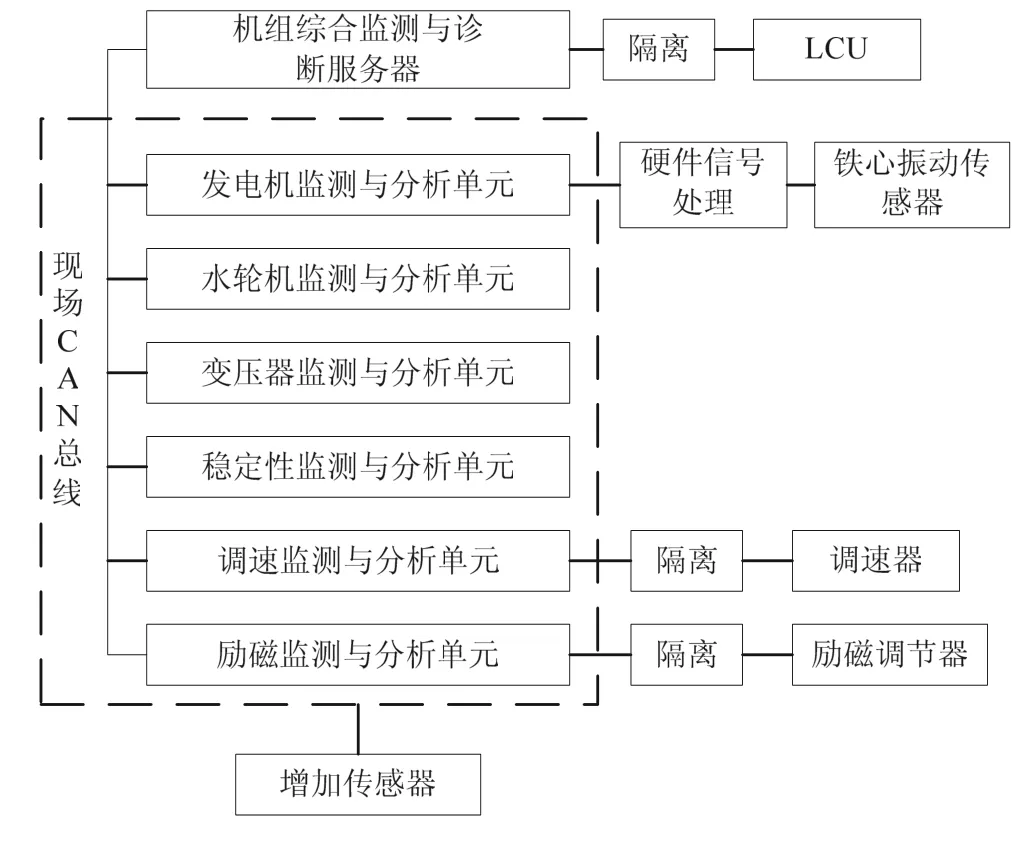
图2 HOMIS结构

只在 HOMIS的硬件上添加了铁心振动位移传感器和硬件信号处理电路，便可实现定子铁心振动的在线监测与分析，其中硬件信号处理电路完成硬件滤波、信号调理等功能，铁心振动分析的实现则在 HOMIS上作软件扩展，主要包括三个方面：

1）信号获取及指标计算在发电机监测与分析单元（以下简称发电机单元）上实现，由于铁心振动属于高速变化信号，HOMIS对铁心振动的采样率选取为1K/s，根据香农采样定理，该采样率能够最大分析振动频率为500Hz的振动信号，满足铁心振动在线监测的要求。

2）机组综合监测与诊断服务器（以下简称机组服务器）完成了集成分析环境下的铁心振动分析。其中机组运行状态参数的获取通过实时性能好、可靠性高的CAN网实现。集成环境下铁心振动分析中的实验参考数据、专家知识等经数字化后直接存储在机组服务器上[13]，其他相关信息的来源见表2。

表2 铁心振动分析相关量的获取途径

3）采用分布式存储策略，指标数据存储在机组服务器上，振动原始数据则存储在发电机单元上。专家可根据需要通过机组服务器向发电机单元申请原始数据。当发电机单元检测到机组工况变化（比如机组并网同期）时，自动根据设定的协议向机组服务器发送原始振动数据。

5 现场监测结果

在葛洲坝水力发电厂的 10台机组上安装了HOMIS，并实现了铁心振动的在线监测与分析，积累了大量的定子铁心振动数据。图3为某机组在不同运行状况时对应铁心振动的频谱。图4为某机组在升负荷过程中，不同频率对应的振动幅值随有功变化曲线，其中200Hz幅值由于太小，放大10倍后显示。

图5为两台机组在110MW～120MW负荷区间，铁心振动峰峰值随定子温度的变化曲线。由图可得出以下4点结论。

（1）定子铁心的100Hz下振动非常明显，且在机组负载比机组空载时更为剧烈；在机组甩负荷过程中，机组振动特征较其他运行状态复杂得多。

（2）机组的运行时，存在6倍和29倍转频的振动分量，可能是由机组定转子间多处气隙不均匀引起的。

（3）100Hz及200Hz下的振动幅值随负荷的变化规律基本一致，6倍及29倍转频对应的振动随负荷变化趋势比较小，且不明显。

（4）在发电机有功基本一致的情况下，定子铁心振动随定子温度升高呈减小趋势。

图3 发电机在不同运行状况下的铁心振动频谱

图4 加负荷实验下各频率分量的振动随有功变化曲线

图5 铁心振动峰峰值随定子温度变化曲线

6 结语

（1）分析了大型水轮发电机组定子铁心转频振动和极频振动的原因及特征，研究了定子铁心振动与机组运行状况的关系。

（2）设计了水轮发电机组集成监测环境下定子铁心振动的分析方法，并介绍了该分析方法中各个功能模块的具体内容。

（3）利用葛洲坝水力发电厂HOMIS为硬件平台，实现了定子铁心振动在线监测与分析，并给出了监测及分析的结果，其监测结果与理论分析基本一致。

[1]马震岳, 董毓新. 水轮发电机组动力学[M]. 大连:大连理工大学出版社, 2003.

[2]白延年.水轮发电机设计与计算[M]. 北京: 机械工业出版社, 1982.

[3]曲凤波, 孙玉田, 曲大庄. 水轮发电机的不平衡磁拉力[J]. 大电机技术, 1997, (4): 1-4.

[4]黄学君. 水轮发电机定子系统的振动研究: [D].天津: 天津大学.

[5]周理兵, 马志云, 贺建华. 响洪甸抽水蓄能变极同步发电/电动机谐波磁场引起的铁心振动与电磁噪声分析计算[J].大电机技术，2002, (6): 30-36.

[6]辜承林, 陈乔夫, 熊永前. 电机学[M]. 武汉: 华中科技大学出版社, 2001.

[7]万书亭, 唐贵基, 李永刚. 发电机运行状态对定转子径向振动特性的影响分析[J]. 机械工程学报,2006, 42(9): 190-194.

[8]A.A.Tampion, R.L. Stoll, J.K. Sykulski.Variation of turbogenerator stator core vibration with load[J].IEE PROCEEDINGS-C, 1991, 138(5): 389-400.

[9]哈尔滨电工学院电机教研究室. 水轮发电机的振动[J]. 大电机技术, 1974, (1)：5-23.

[10]许实章, 等. 水轮发电机定子铁心的磁振动[J].华中工学院学报, 1973, (12)：45-79，153.

[11]沈旭东.次谐波引起的铁心振动分析[J]. 大电机技术, 1988, (1): 20-25.

[12]F.C.Trutt，J.Sottile，J.L.Kohler. Detection of AC Machine Winding Deterioration Using Electrically Excited Vibrations. IEEE Trans on Industry Applications [J]. 2001，37(1)：10-14.

[13]李朝晖, 杨贤, 毕亚雄. 水电机组数字化及其工程应用[J]. 电力系统自动化, 2008, 32(23): 76-80.

[14]Zhaohui LI, Youzhong AI, Huixuan SHI.Optimal Maintenance Information System of Gezhouba Hydro Power[C]// In Proceedings of 2007. IEEE Power Engineering Society General Meeting, 2007.