基于Simulink的无刷直流电机仿真模型新策略
2010-06-28陈晋玮
陈晋玮
(船舶重工集团公司 723所,扬州225001)
0 引 言
随着电力电子、集成电路、电机控制理论和永磁材料的快速发展,永磁无刷直流电机广泛应用于工业控制的各个领域。永磁无刷直流电机结构简单、运行可靠、维护方便,具有良好的调速性能。为了便于理论分析和验证各种控制算法和策略,正确建立直流无刷电机控制系统的模型就显得非常重要。本文利用Matlab软件下Simulink仿真工具箱对直流无刷电机控制系统进行详细的建模与仿真,克服了用电力系统模块库分析不够深入、仿真欠灵活等缺点。仿真结果表明该仿真模型与理论分析相吻合,验证了仿真模型的正确性和有效性。
1 无刷直流电机的数学模型
无刷直流电机的运行特性涉及非线性理论及数值解法等诸多问题,在一般工程应用上通常均作如下假定:(1)各相绕组对称,其对应的电路单元完全一致,相应的电气时间常数忽略不计;(2)忽略齿槽、换相过程和电枢反应等的影响;(3)控制电路在开关状态下工作,功率开关管为理想开关,功耗不计;(4)磁路不饱和,不计涡流和磁滞损耗。
由于直流无刷方波电动机的气隙磁场、反电动势以及电流是非正弦的,因此采用d-q变换已不是有效的分析方法,通常直接利用电动机本身的相变量来建立数学模型。
1.1 电压方程
BLDCM三相定子电压的平衡方程可以用以下的状态方程表示:
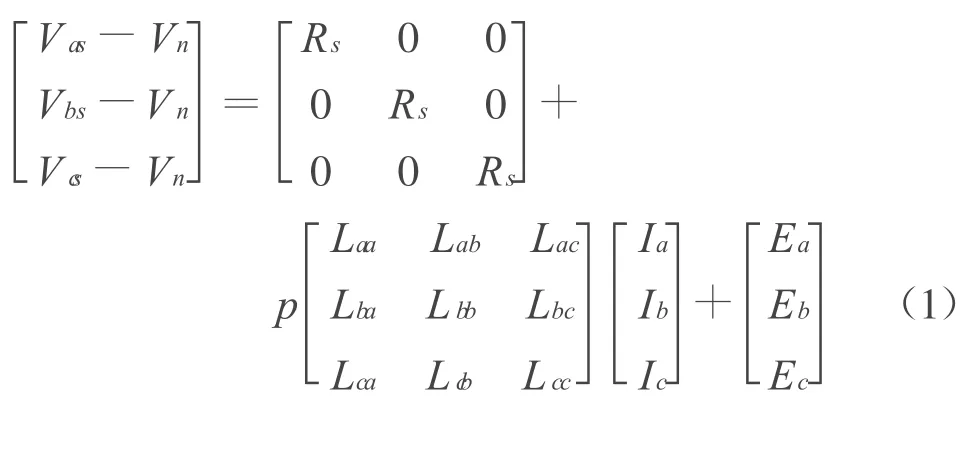
式中:Rs为三相定子绕组的相电阻;Ia,Ib,Ic为三相定子相电流;Laa,Lab,Lac,Lba,Lbb,Lbc,Lc a,Lc b,Lcc为三相定子绕组之间的互感;Ea,Eb,Ec为三相定子的反电动势;p为微分算子;Vn为三相定子绕组中点电压:

式中:∑ES为瞬时三相定子的反电动势之和,反电势为理想梯形波,幅值为:

式中:B为磁场强度;L为电机长度;N为每相匝数;ω为电机转动角速度。
这里假设电感不随位置而改变,反电势为理想梯形波。在360°电角度内,转子的磁阻不随转子位置的变化而变化,并假定三相绕组对称,则有Ia+Ib+Ic=0,并有:
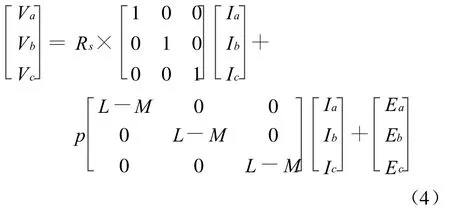
式中:Ea,Ec,Ec为三相反电动势信号。
1.2 转矩方程和运动方程
转矩方程为:
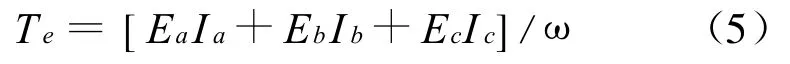
运动方程为:
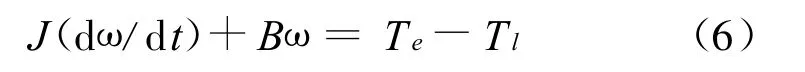
式中:T1为负载转矩;J为转动惯量;B为摩擦系数。
电机转动角度函数为:dθ/dt=(P/2)×ω,P为电机极数。
2 基于Simulink的BLDCM 控制系统模型的建立
目前,Simulink仿真平台由于操作简便、模型库丰富、仿真效率较高等优点,得到科技界广泛认可。本文充分利用 Simulink现有资源,在分析BLDCM数学模型的基础上,对永磁无刷直流电机建模原理和实现过程进行了详细阐释。其系统框图如图1所示。BLDCM控制系统仿真模型主要包括:BLDCM本体模块、速度控制模块、触发逻辑控制驱动逆变模块和转矩计算模块。通过这些功能模块的有机整合,成功搭建出了BLDCM控制系统的仿真模型,并实现了闭环的控制算法。

图1 BLDCM控制系统仿真模型
2.1 BLDCM本体模块
BLDCM系统状态方程为 X′=AX+Bu,由式(7)、(8)、(9)、(10)、(11)建立在整个控制系统的仿真模型中。BLDCM 仿真模型如图2。
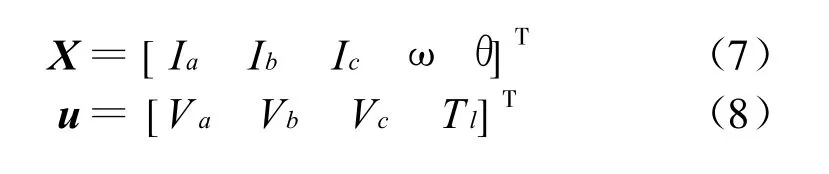

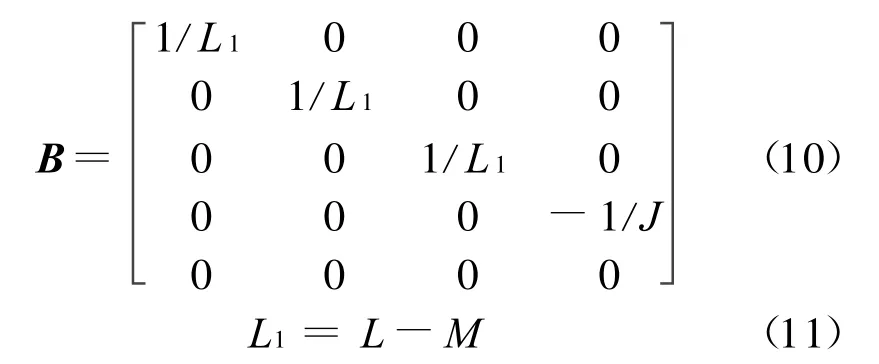

图2 BLDCM仿真模型
BLDCM本体模块是最重要的部分,该模块根据BLDCM电压方程式(4)求取BLDCM三相相电流,由式(4)可得,要获得三相相电流信号 Ia、Ib、Ic,首先要求得三相反电动势信号 Ea、Eb、Ec。在BLDCM建模过程中,梯形波反电动势的求取方法一直是较难解决的问题,反电动势波形不理想会造成转矩脉动增大、相电流波形不理想等问题,严重时会导致换向失败,电机失控。因此,获得理想的反电动势波形是BLDCM仿真建模的关键问题之一。
S函数模型提供了了解电机内部情况的手段,只要电机数学模型足够精细,就能够通过仿真观察到电机内部的仿真结果,因此该模型在建模分析时具有较大的灵活性。本模块S-function采用分段线性法建立梯形波反电动势波形,将一个运行周期0~360°分为 6个阶段 ,每 60°为一个换向阶段,每一相的每一个运行阶段都可用一段直线进行表示,根据某一时刻的转子位置和转速信号,确定该时刻各相所处的运行状态,通过直线方程即可求得反电动势波形。分段线性法简单易行且精度较高,能够较好地满足建模仿真的设计要求。
2.2 速度和转矩计算模块
速度和转矩计算模块如图3所示。该模块采用了通用的PID调节器进行速度和电流的控制。根据速度给定信号、速度反馈信号,用编程S-function计算所需力矩和电机定子每相电流。

图3 速度和转矩计算模块
力矩公式为:
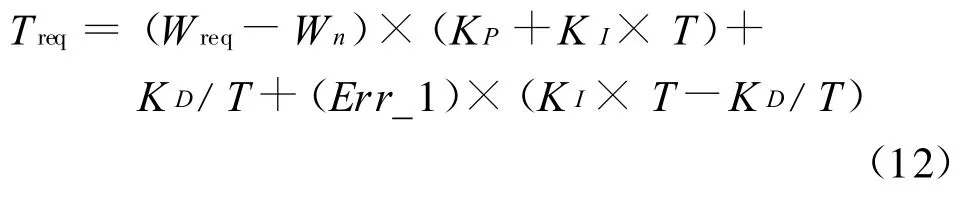
式中:Treq为给定速度所需力矩;Wn为反馈速度;Wreq为给定速度,KP、KI、KD分别为比例、积分和微分参数;Err_1为前一时刻的速度误差。
电流公式为:

2.3 换相逻辑模块
BLDCM控制系统中逆变器的可靠换相,是通过BLDCM内部的转子位置信号进行控制的。IUSTAR_in,IVSTAR_in,IWSTAR_in和反电动势波形相似,包含了转子位置信息。该模块包含三个子模块(如图4),均用Stateflow Charts图形化建立两相导通三相六状态BLDCM换相逻辑。
3 仿真试验及结果
根据上述所建立的BLDCM控制系统的仿真模型,进行了转速调节的仿真试验。仿真所用电机数据:定子绕组电阻Rs=0.702 9 Ω,相电感 L-M=4.238mH,转动惯量J=2kgcm2,额定电流I=4.5 A,额定转速n0=480 rpm,额定转矩 T=6 Nm,极对数 P=2。仿真条件:采用多步解算器ode113算法,变步长。

图4 换相逻辑仿真模型
从图5可以看出,系统从零速启动时,仿真模型S-function需要时间计算反电动势来确定转子位置,之后保持最大启动转矩,转速响应有超调,系统在很短的时间内就进入了稳态。仿真结果显示稳态运行时转速无静差,与理论情况相吻合。由仿真波形可以看出,在N=75 rpm的参考转速下,系统响应快速且平稳,系统具有较好的静、动态特性。仿真结果证明了本文所采用这种BLDCM仿真建模方法的有效性,同时也证实了反电动势控制法的可行性。
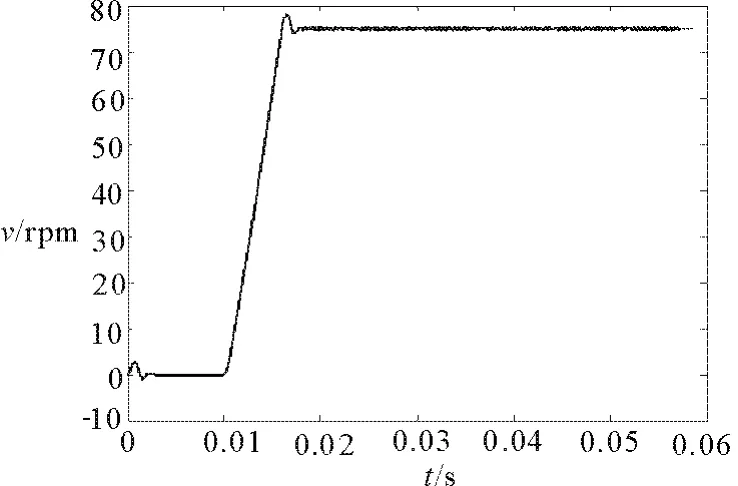
图5 系统速度相应曲线
4 结论
本文在分析BLDCM数学模型的基础上,先后对永磁无刷直流电机的电路模型和S函数模型的建模原理及实现方法进行了阐述,建立了BLDCM控制系统仿真模型。在上述仿真的基础上,控制器可采用不同的控制算法,通过该仿真系统的响应来验证和改进控制策略,它为分析和设计直流无刷电机控制系统提供了一个理想试验平台。
[1]Krishnan R.Electric motor drives-modeling,analysis and control[M].New Delhi:Prentice Hall of India Private Limited,2005.
[2]陶桂林,马志云,周理兵,等.永磁无刷电机的建模与仿真分析[J].华中科技大学学报,2003,31(1):82-85.[3]吴影生,胡虔生.无刷直流电机系统仿真模型与改进[J].机械制造与自动化,2003(5):54-57.
[4]张琛.直流无刷电动机原理及应用[M].北京:机械工业出版社,1996.
