EM方法的一种修正及应用

向绪言, 刘丽芳

(湖南文理学院 数学与计算科学学院, 湖南 常德, 415000)

EM方法的一种修正及应用

向绪言, 刘丽芳

(湖南文理学院 数学与计算科学学院, 湖南 常德, 415000)

针对删失数据的参数估计问题, 给出了EM方法的一种修正. 对Poisson过程情形, 理论上证明由该方法得到的估计是无偏估计, 并给出了相应的置信区间；对一般情形, 通过该方法在计算神经科学解码研究中的应用举例, 说明该方法得到的估计比通常EM方法得到的估计好.

删失数据；EM；修正EM

极大似然估计(Maximum Likelihood Estimate,即MLE)是一种常用的点估计，在总体分布形式复杂时, 不可能找到显示解, 这时需要用更复杂的方法——EM(Expectation Maximization)方法. 然而在样本数据具有删失的情况下, 用通常的EM方法会失败. 例如：在计算神经科学的解码研究中[1-3], 需要利用神经元的已知反应提取相应刺激的参数信息,实验中, 用固定的时间窗口观测并记录神经元的spike发放(fire)时间, 由于实验本身限制, 时间窗口通常很小, 所以得到的ISIs(Interspike intervals, 即spikes时间间隔)是删失数据. 这样, 由通常的EM方法得到刺激的估计与实际刺激误差很大, 于是给出了针对这种删失数据的一种修正EM方法. 对Poisson过程情形, 理论上证明由该方法得到的估计是无偏估计, 并给出相应的置信区间；对一般情形,通过该方法在计算神经科学解码研究中的应用举例,说明该方法得到的估计比通常EM方法得到的估计好.

1 MLE和EM方法

1.1 MLE

根据p( x| Θ)的不同, 其求解的难易程度不同.例如, p( x| Θ)是单个的正态分布, Θ=(μ, σ2)时很容易求解. 然而, 有许多这样的问题, 我们不可能得到其显示解, 于是需要用到更复杂的技巧——EM方法.

1.2 EM方法

当样本数据不完全或有缺失时, EM算法是求解极大似然估计的常用方法. 仍然假设X是一些分布的样本数据, 此时X是不完全数据. 记其完全数据集为Z( X, Y), 联合密度函数为：

1.3 混合分布的EM方法

考虑如下混合密度参数模型：

2 修正EM方法

解码是计算神经科学中的重要方面, 其目的是利用神经元的已知反应(response)提取相应刺激(stimulus)的参数信息, 因为对于给定的神经元, 接受不同的刺激, 其反应也不同；而神经元的反应表现在spikes变化上, 包括spikes的发放频率(firing rate)和spikes之间的时间间隔(Interspike intervals, ISIs).一项重要的研究工作就是根据神经元的ISIs序列估计其密度函数的参数(通常与输入的刺激有关). 具体做法是：

实验中, 用固定的时间窗口T观测并记录神经元每个spike发放的时间, 得到ISIs序列{ti, τi, σi} (图1, {τi},{σi}是不完整数据), 称为删失数据. 由于实验本身限制, 时间窗口通常很小, 所以由EM方法得到刺激的估计与刺激真值误差很大.

图1 删失数据

3 Poisson过程下修正EM的无偏性与置信区间

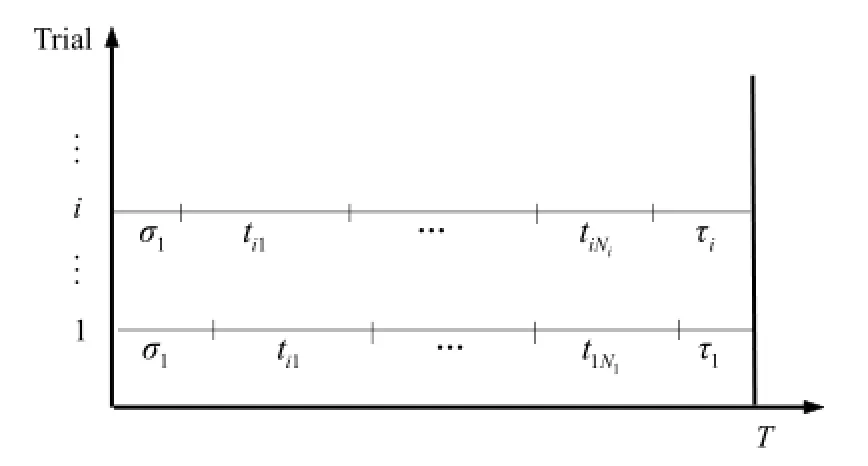
图2 来自Poisson过程的删失数据

4 修正EM方法在神经元解码中的应用

用500 ms的时间窗口截取1 438个trial, 共产生3 000个ISIs, 其中, 规则数据1 676个, 截断数据1 324个, 超过25%的trials(362个)只有1个spike(图3). 频率直方图见图4.

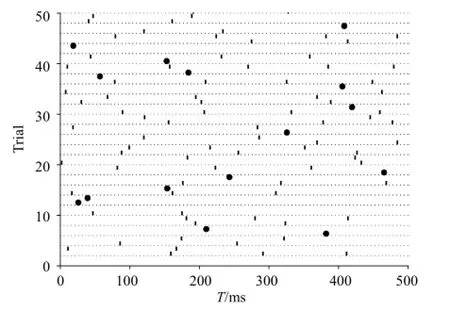
图3 模拟产生的前50个trials

按通常的EM方法求得MLE为：

图4 频率直方图

由式(11)、(12)、(13)和图4易知：用通常的EM方法失败, 而修正EM方法成功.

[1] Feng J F. Computational Neuroscience—A Comprehensive Approach[M]. London FL： Chapman and Hall Press, 2003： 341-366.

[2] Feng J F, Ding M. Decoding spikes in a spiking neural network[J]. Journal of Physics A： Math and Gen, 2004, 37：5713-5727.

[3] Tuckwell H C. Introduction to Theoretical Neurobiology [M]. Cambridge： Cambridge University Press, 1988：191-246.

[4] Lehmann E, Casella G. Theory of Point Estimation[M]. Berlin： Springer, 1999： 109-128.

[5] 茆诗松, 王静龙, 濮晓龙. 高等数理统计[M]. 北京： 高等教育出版社, 1999： 428-443.

[6] 何声武, 谢盛荣, 程依民. 随机过程[M]. 北京： 中国统计出版社, 1997： 34-50.

A correction for EM method and its application

XIANG Xu-yan, LIU Li-fang
(College of Mathematics and Computing Science, Hunan University of Arts and Science, Changde 415000, China)

For parameter’s estimate with censored data, a correction for EM method is proposed. In the case of Poisson process, we prove in theory that the estimate obtained by this method is unbiased. The corresponding confidence interval is given. Generally, examples which the method for decoding is unable in neuroscience to show that the estimate obtained by this method is better than maximum likelihood estimate, are included.

censored data; EM; EM with correction

O 211.67

：A

1672-6146(2010)04-0003-04

10.3969/j.issn.1672-6146.2010.04.002

2010-09-10

国家自然科学基金(10871064); 湖南省自然科学基金(09JJ6016); 湖南省教育厅优秀青年项目(10B073)

向绪言(1975-), 男, 博士, 副教授, 研究方向为随机过程及生物信息.