非线性网络化控制系统鲁棒容错控制＊

兰州理工大学电气工程与信息工程学院（甘肃 兰州730050）李 炜 蒋栋年

1 引言

网络化控制系统（Networked Control System，NCS）是通过一个实时网络构成的闭环控制系统。与传统意义上点到点连接的控制系统相比，NCS具有连线少，成本低，资源共享，便于系统安装、维护、扩展和故障诊断等优点[1-2]。然而，由于网络的引入也衍生出诸如数据传输时延、丢包、异步采样、多包传输、时序错乱以及网络调度等新问题[3]。此外，NCS不仅规模更加庞大、结构复杂，而且不确定因素众多，一旦发生故障，损失将难以估量，因此使NCS具有容错能力已成为现代网络化控制系统的本征性能所求[4]。近年来NCS的容错研究越来越受到广泛的关注[5-7]，但是目前的研究大多数限于线性系统，非线性系统的研究则一般采用T-S模糊模型[8，9]。T-S模糊模型[10]是将线性系统理论与模糊理论相结合来解决非线性系统问题的方法，通过IF-THEN规则将复杂的系统用若干局部的线性模型来表示，再以局部模型的综合来完成全局模型的构造。

本文针对线性连续网络化控制系统，基于时延准T-S模型，考虑系统参数不确定性的影响，在传感器发生失效故障时，通过构造时延概率分布相关的Lyapunov泛函，给出了系统具有鲁棒完整性的充分条件，并通过求解LMIs得到了鲁棒容错控制器。

2 系统描述

2.1 网络化控制系统的T-S模型

考虑线性被控对象

式中：x(t)∈Rn，u(t)∈Rm分别为被控对象状态变量和控制向量，系数矩阵 A，B，C具有适当的维数。根据文献[11]，假设传感器和执行器均由时钟驱动，设 h为采样周期，由离散化式(1)可以得到 kh时刻的网络控制系统的局部模型

其中：执行器的 kh时刻采样的数据包的网络时延为 τk(k∈N)个周期，且

假设maxτk=n(n∈N)，且数据包按照发送顺序到达控制器和执行器，那么 τk+1只决定于 τk，而与 τ1，τ2，…，τk-1无关，即{τ1，τ1，…τk，…}构成一个马尔可夫链。考虑到网络时延 τk的随机性，设 k时刻网络时延概率分布为 μ(k)=[μ1(k)，μ2(k)，…，μn(k)]，其中 μi(k)=P(τk=i)。若 T=[pij](i，j∈{1，2，…，n})为马尔可夫时延概率转移矩阵，初始值 μ(0)已知，则 μ(k+1)=μ(k)T，则可根据 T和 μ(0)来求得 k时刻的模型概率分布 μ(k)。

将具有 τk=i时的模型视为一个子系统，随机变量 τk的概率分布作为隶属度函数，若对各子系统使用相同的状态反馈控制律，模糊规则可以如下方式给出

THEN网络控制系统局部模型为

应用并行分布补偿（PDC）方法，网络控制系统的全局模型可表示为

由式(3)可以得到网络化控制系统的时延准T-S闭环模型为

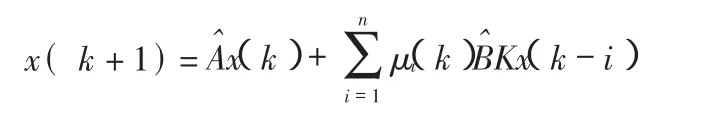
在实际的网络化控制系统，由于环境的变化、元器件的老化、网络指标的精确度等原因，系统往往具有不确定性，考虑具有参数不确定性的系统

其中ΔA和ΔB是范数有界的，由(3)，(4)可得不确定网络化控制系统的闭环模型为

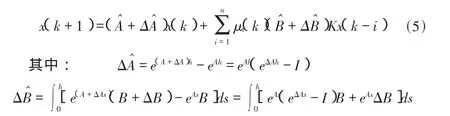
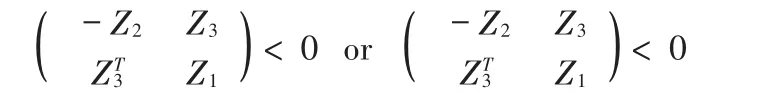
引理3[14]给定矩阵 Z1，Z2和 Z3，若

2.2 引理

引理1[12]对任意的变量 v1，v2和矩阵 M和正定对称矩阵 N，由(Mv1-Nv2)TN-1(Mv1-Nv2)≥0可得

引理2[13](schur补引理)若已知3个矩阵Z3则，当且仅当，当且仅当，对于

3 主要结果

执行器失效故障时NCS鲁棒容错控制：

考虑传感器可能发生失效故障的情形，引入开关矩阵 F，并把它放在反馈增益阵和状态之间，其形式为

F∈Φ，Φ为传感器开关矩阵 F的对角元素任取0或1的各种组合的对角阵集合（除 F=0外），表示所有可能的传感器失效故障模式的集合。则网络化闭环故障系统模型为

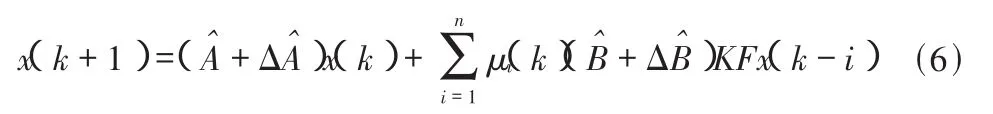
鲁棒容错控制的设计目标为：寻求状态反馈增益阵K，使得不确定网络化闭环故障系统对任意 F∈Φ均保持渐近稳定。

定理1对于任意可能的传感器失效故障模式 F∈Φ和系统允许的不确定性，给定正定对称矩阵 R以及正常数 α，β，若存在正定矩阵 X，满足

则系统(6)对传感器失效故障具有鲁棒完整性。控制器增益矩阵即为 K。

证明：考虑闭环系统(6)构造离散Lyapunov-Krasovskii泛函

由引理1可得

则ΔV(k)＜0，即系统(6)是渐近稳定的。

对(9)，(10)分别左乘和右乘 P-1，并定义 X=P-1，则有

注：定理1中所得到的条件不是严格的LMI条件，使得式(14)成为非凸问题，不能直接采用LMI求解的方法求解。

求解该非线性优化问题的步骤如下

Step1：选取 P-1=λI，其中 λ＞0为充分大的常量，设 s=1；

Step2：使用Step1中选取的 P-1求解LMI(7)，(8)；

Step3：令 P-1=X，重新求解 LMI(7)，(8).s=s+1；

Step4:判断条件：若|δs- δs-1|＜ξ，或|γs- γs-1|＜ξ，停止；否则，返回Step2。其中 ξ为预先选定的充分小量。

4 仿真实例

考虑网络化控制系统(4)，(5)采用如下的模型数据

设采样周期为 h=0.1s，并假设 maxτk=3，μ(0)=[0.3，0.4，0.3]，65 个周期后，μ(65)=[0.2308，0.4615，0.3077]，则 T-S 网络化控制系统的全局模型如下

针对传感器正常和各种失效故障情形，其中：F0=diag(1，1)表示传感器正常情况，F1=diag(0，1)和 F2=diag(1，0)分别表示传感器1，2发生完全失效故障。根据定理1，取 α=1，β=1求解线性矩阵不等式组LMIs，可得

假设系统的初始条件为 x(0)=[3，3]T，在传感器发生 F1和F2故障情形下，其状态 x1，x2的零输入响应如图1，图2所示。

由仿真结果可以看出，NCS在发生传感器失效故障时仍是渐近稳定的，说明文中所述方法对于具有马尔可夫特性时延的影响，不确定网络控制系统在传感器失效故障时具有鲁棒完整性。

5 结论

本文以具有马尔可夫特性时延的网络化线性控制系统为研究对象，基于时延准T-S模型，考虑系统参数不确定性的影响，采用状态反馈控制律，在构造Lyapunov-Krasovskii泛函时引入了时延概率分布因子，推证出了保证参数不确定网络化控制系统在传感器发生失效故障时仍渐近稳定的充分条件，并以求解LMIs给出鲁棒容错控制器的设计方法。最后通过仿真验证了文中所述方法的可行性和有效性。

[1]Zhang W，Branicky M，Phillips S.Stability of networked control systems[J].IEEE Control Systems Magazine，2001，21(1):84 ～ 99.

[2]Walsh G.C.，Hong Ye，Bushnell L.G.Stability analysis of networked control systems[J].IEEE Transactions on Control Systems Technology，2002，10(3):438～446.

[3]邱占芝，张庆灵，刘明.有时延和数据包丢失的网络控制系统控制器设计[J].控制与决策，2006，21(6)：625 ～ 630.

[4]R J Patton，C.Kambhampati，A.Casavola，G.Franze.Fault-tolerance as a key requirement for the control of modern systems[J].The International Federation of Automatic Control，2006，6(1):26 ～ 36.

[5]郑英，王彦伟，方华京.基于T-S模型的网络化控制系统的鲁棒容错控制[J].华中科技大学学报，2008，36(3)：111 ～113.

[6]Huo Zhihong，Fang Huajing.Research on robust fault-tolerant control for networked control system with packet dropout[J].Journal of Systems Engineering and Electronics，2007，18(1):76 ～ 82.

[7]郭一楠，张芹英，巩敦卫，张建化.一类时变时延网络控制系统的鲁棒容错控制[J].控制与决策，2008，23(6):689 ～692.

[8]Huaguang Zhang，Jun Yang，Chun-Yi Su.T-S Fuzzy-Model-Based Robust Design for Networked Control Systems With Uncertainties.Industrial Informatics，IEEE Transactions 2007，3(4):289 ～ 301.

[9]Huaguang Zhang，Dedong Yang，Tianyou Chai.Guaranteed Cost Networked Control for T-S Fuzzy Systems With Time Delays.Systems，Man，and Cybernetics，Part C:Applications and Reviews，IEEE Transactions on Volume 37，Issue 2，March 2007 Page(s):160 ～ 172.

[10]Takagi T，Sugeno M.Fuzzy identification of systems and its applications to modeling and control[J].IEEE Transaction on system，Man，and Cybernetics，1985，15:116 ～ 132.

[11]Zheng Y，Fang H，Wang H.Takagi-Sugeno fuzzy model-based fault detection for networked control systems with Markov delays[J].IEEE Transactions on System，Man，and Cybernetics，Part B:Cybernetics，2006，36(3):924～929.

[12]Fang Huajing，Zhang Hong，Fang Yiwei，et al.Quasi T-S fuzzy models and stable controllers for networked control systems[C].The 6th World Congress on Intelligent Control and Automation，Dalina China，2006.

[13]Gemain G，Jacques B，Denis A.Robust stabilization of discrete-time linear systems with norm-bounded time-varying uncertainty.IEEE Trans.Systems and Control Letters，1994，22(5):327 ～ 339.

[14]Mahmoud M.S.Robust control of discrete systems with uncertain parameters and unknown delay.IEEE Trans.Automatica，2000，36(4):627 ～ 635.