基于HALCON的摄像机标定*
2010-06-25罗珍茜孙峰杰陆士清李长远
罗珍茜,薛 雷,孙峰杰,陆士清,李长远
(上海大学 通信与信息工程学院,上海 200072)
1 引言
近年来,主动视觉在动态目标监控与跟踪、合作目标与非合作目标位置测量,以及工业生产线监测中有着广泛的应用。在主动视觉中,摄像机焦距、光学中心以及外参数是可变的,这些参数的动态在线标定在主动视觉中有重要作用。要利用摄像机进行视觉感知获取目标的三维信息,就必须进行摄像机标定,以确定摄像机的参数[1]。摄像机标定是指建立摄像机图像像素位置和场景点位置之间的关系,其途径是根据摄像机模型,由已知特征点的图像坐标和世界坐标求解摄像机的模型参数[2]。精确标定摄像机内外参数不仅可以直接提高测量精度,而且可以为后续的立体图像匹配与三维重建奠定良好的基础。
国内外许多学者提出了摄像机标定的方法,并得到广泛应用。传统的摄像机标定方法采用的是基于3D立体靶标的摄像机标定,但是3D立体靶标制作成本高,制作方法复杂。Roger Tsai[3]提出基于径向约束的两步法,该方法计算量适中,精度较高。张正友提出基于2D平面靶标的摄像机标定法,该方法克服了3D靶标的缺点,且标定过程中摄像机拍摄角度改变对标定结果无影响。HALCON是德国MVtec公司开发的图像处理软件,它具有完善的综合标准软件库和机器视觉集成开发环境。HALCON提供了丰富的函数库,包括blob分析、形态学、模式匹配、测量、三维目标识别和立体视觉等。它支持Windows,Linux和Solaris操作环境,整个函数库可以用C,C++,C#,Visual Basic 和 Delphi等多种普通编程语言开发,有效提高了开发效率,并且执行速度快,具有良好的跨平台移植性。
2 摄像机模型
为了标定摄像机,首先需要建立一个模型将世界坐标系中三维空间点投影到二维图像中,该模型由摄像机和镜头组成。在机器视觉应用中常用到的两种摄像机模型为面阵摄像机模型和线阵摄像机模型。线阵摄像机模型相对面阵摄像机模型要复杂许多,笔者介绍的是常用的面阵摄像机模型。在实际应用中,通常使用针孔摄像机,它的面阵摄像机模型如图1所示。其中,图像坐标系(r,c),成像平面坐标系(u,v),摄像机坐标系(xc,yc,zc),世界坐标系(xw,yw,zw),Sx和 Sy是缩放比例因子,它们表示图像传感器上水平和垂直方向上相邻像素之间的距离。f表示的并不是镜头的焦距,而是摄像机主距。点P是世界坐标系中点Pw在成像平面上的投影。
世界坐标系中的点 Pw=(xw,yw,zw)T变换到它在成像平面坐标系上的投影点P,需要经历以下4个步骤:
1)点 Pw=(xw,yw,变换到摄像机坐标系中的点Pc=(xc,yc,, 关系为 Pc=RPw+T。 T=(tx,ty,是一个平移向量,R=R(α,β,γ)是一个旋转矩阵,α,β,γ 是分别绕摄像机坐标系 x,y,z轴的旋转角度。在R和T中6个参数(α,β,γ,tx,ty,tz)称为摄像机外参、外方位参数或摄像机位置,它们决定了摄像机坐标系与世界坐标系之间的相对位置。
2)摄像机坐标系中点Pc变换到成像平面坐标系,它们之间是透视投影关系
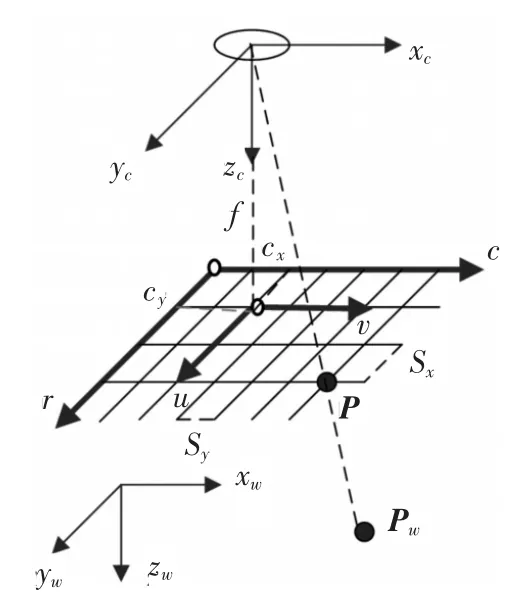
图1 针孔摄像机模型

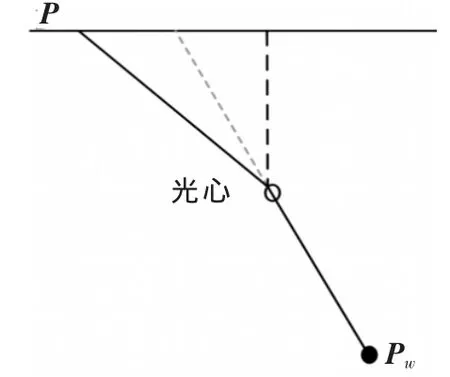
图2 镜头畸变
3)在不考虑镜头畸变的情况下,世界坐标系中的点Pw与成像平面中的投影点P之间的直线过摄像机光学中心,如图2所示。
大部分情况下,镜头的畸变可以近似为径向畸变,即
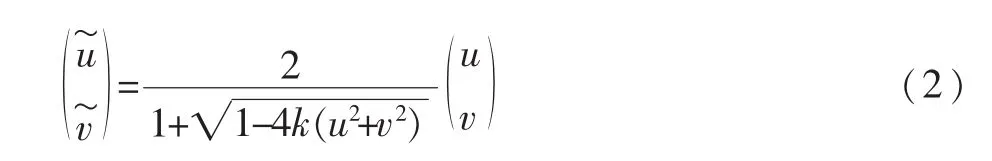
其中,参数k决定了径向畸变的程度,如图3所示。
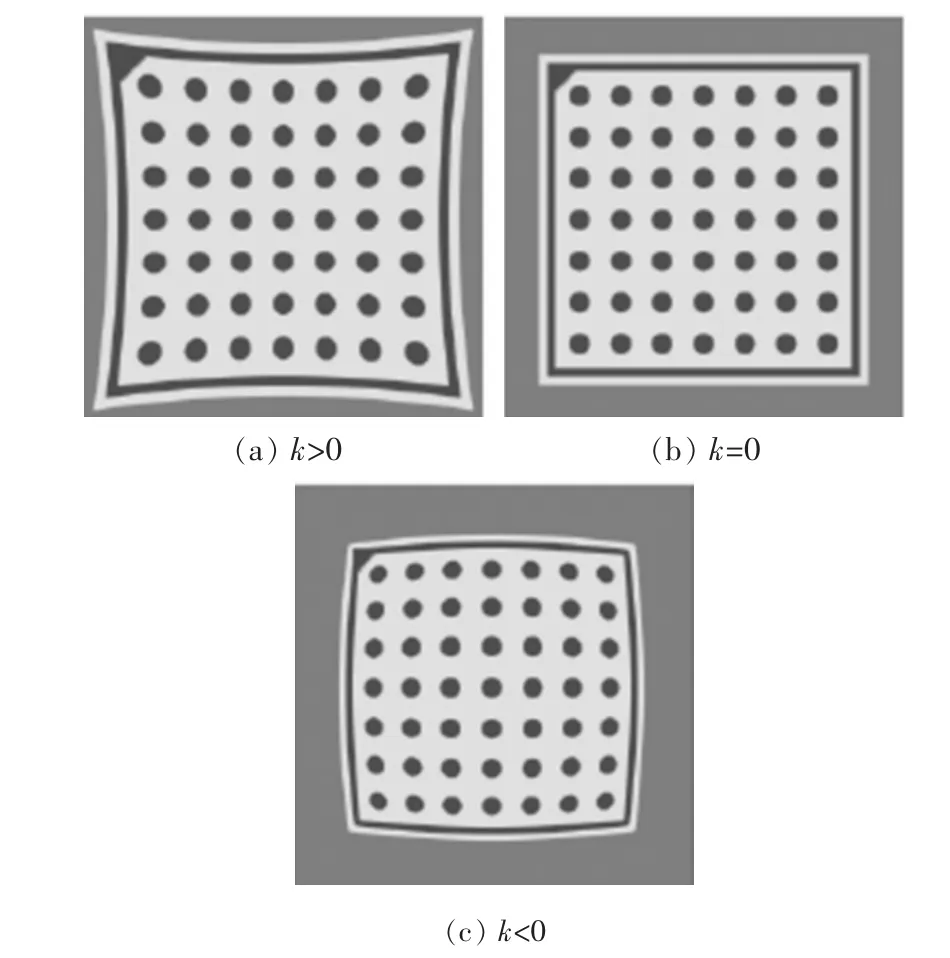
图3 3种情况下的镜头畸变

式中:(Cx,Cy)T是光心在成像坐标系中的投影点。
由以上可知,摄像机标定的实质就是确定内部参数(f,k,Cx,Cy,Sx,Sy)和外部参数(α,β,γ,tx,ty,tz)的过程。
3 基于HALCON的标定
为了进行摄像机标定,必须已知世界坐标系中足够多的三维空间点的坐标,找到这些空间点在图像中的投影点的二维图像坐标,并建立对应关系[4]。这就要求标定过程必须满足两个要求:1)放置在已知位置上的容易提取特征的目标物体或标志(标定板);2)确定世界坐标系中已知点与它们在投影图像中的对应关系。
3.1 标定板
标定板的选择决定了标定的精度,为了达到较高精度,可以从以下方面考虑标定板的选择:
1)标定板的材质:光源在标定板前方,选择陶瓷标定板;光源在后方,选择玻璃标定板。
2)标定板的尺寸:标定板的形状通常为正方形,宽度应接近图像宽度的1/3。例如,图像大小为100 mm×80 mm,标定板尺寸选择30 mm×30 mm较为合适。
HALCON提供了标准的标定板模板,如图3b所示,该标定板的特点是:标定板周围的黑色矩形框使得标定对象的中心容易被提取;矩形边界框角落的方向标记使得标定板的方向唯一。每块标定板都应该有一个对应的描述文件CalTabDescrFile,它描述了标定板的行数和列数、标定板外框的几何尺寸、方向标记、标定板圆形标志的半径等信息。选择到合适的标定板后,用gen_caltab函数生成对应的标定板描述文件。
3.2 提取特征
利用标定板的特点,提取目标板特征,其过程如下:摄像机提取标定板的一帧图像后,首先通过简单的阈值分割算法就能将标定板的内部区域与背景分离;其次利用Canny滤波器提取标定板各圆形标志的边缘;再次采用Fitzgibbon[5]提出的通过线性方法来最小化代数误差以得到拟合椭圆,该算法具有很好的稳健性,可以抑制边缘中孤立点对边缘拟合的影响;最后提取出椭圆的最小外接四边形,可以很容易确定标志点及其与图像中的投影之间的关系。
3.3 摄像机标定
进行摄像机标定时,标定精度与图像数量有关,至少选择10~15幅。所选图像中标定板的位置应该能覆盖图像的4个角,因为角落处的镜头畸变最大,这样能得到较准确的畸变系数k。
标定过程中,由于使用的是平面标定对象,还会存在这样的问题:如果标定对象平行于成像平面,f和tz的解不唯一。解决方法是在最优化过程中保持Sy不变。
基于HALCON的标定过程如图4所示,read_image(∶Image∶FileName∶)读取名称为 FileName 的图像 Image;find_caltab(Image∶Caltab∶CalTabDescrFile,SizeGauss,Mark Thresh,MinDiamMarks∶)通过 3.2节介绍的算法提取图像Images中标定板上的圆形标志来确定标定板的有效区域, 效果如图 5a所示;find_marks_and_pose(Image,CalTabRegion∶∶CalTabDescrFile,StartCamParam,StartTh resh,DeltaThresh,MinThresh,Alpha,MinContLength,Max DiamMarks∶Rcoord,Ccoord,StartPose)确定标定板上圆形标志点的二维坐标,并得到摄像机外部参数的初始值,效果如图 5b 所示;camera_calibration(∶∶NX,NY,NZ,Nrow,Ncol,StartCamParam,NstartPose,EstimateParams∶CamParam,Nfinal Pose,Errors)计算出摄像机的所有参数,它是通过提供的初始参数为初始值,进行优化搜索获得误差最小化的过程;write_cam_par( ∶∶CamParam,CamParFile∶)将标定结果写入CamParFile文件。
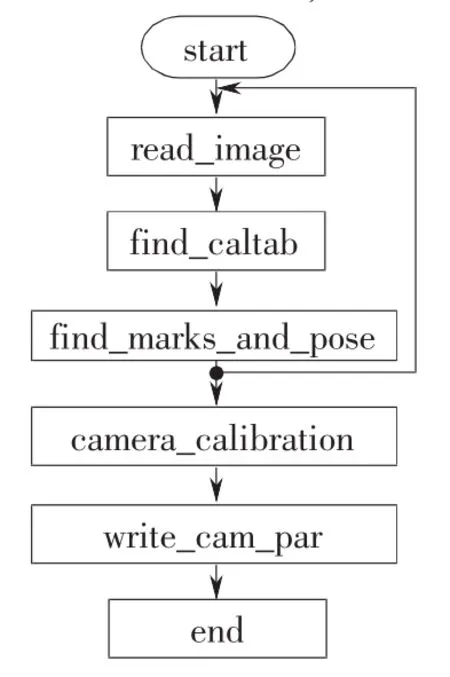
图4 程序流程图

图5 标定效果
HALCON强大的图像处理能力,为摄像机自主标定提供了简单有效的方法。
4 实验结果分析
根据上述标定原理和开发步骤,在Windows XP平台下利用VC++6.0开发了一个基于HALCON8.2的摄像头标定程序,程序经过严格测试,运行稳定,在黑背景下截取3组数量不同的320×240的标定板图像用于标定,并通过重投影法分析标定结果的平均误差。
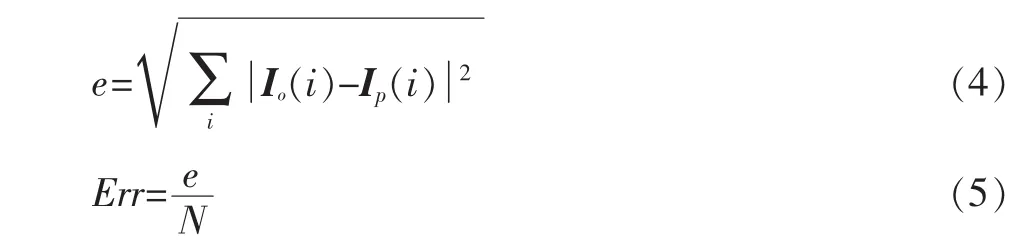
式中:e表示均方误差;Io(i)表示原始图像上第i点的向量,Ip(i)表示重投影图像上第 i点的向量,i∈(0,N);N 表示标志点总数,例如利用10幅标定板图像进行标定,则N=10×7×7;平均均方误差Err等于均方误差与标志点总数的比值。
结果如表1所示,效果较好,可以达到使用要求。
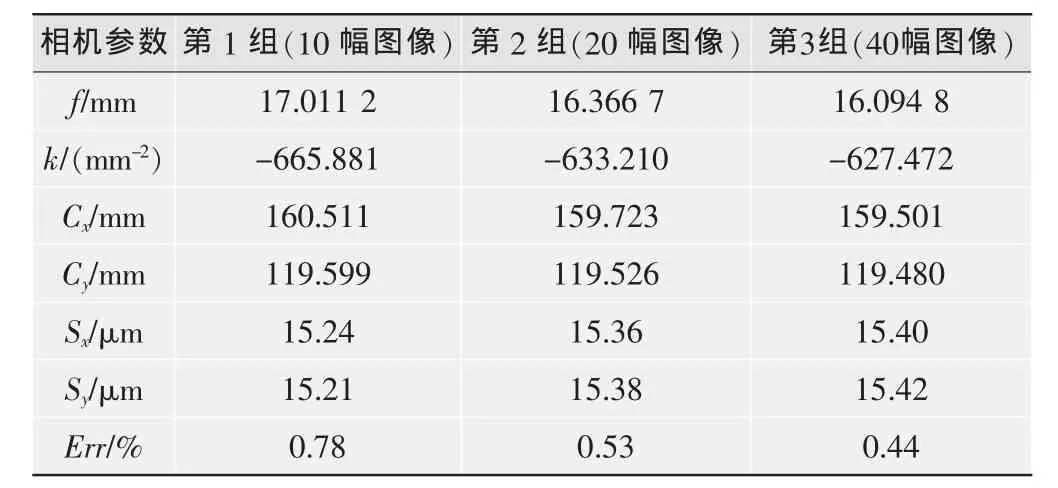
表1 标定结果比较
5 小结
基于HALCON开发的摄像机标定程序在实际运用中取得了很好的效果,标定结果精确、运算效率高、跨平台移植性好,操作简单,缩减了开发周期,可以有效地应用于各种计算机视觉系统中。
[1]李良福,陈卫东,冯祖仁,等.目标跟踪与定位中的视觉标定算法研究[J].应用光学,2008,29(4):481-486.
[2]张广军.机器视觉[M].北京∶科学出版社,2005.
[3]TSAI R Y.An efficient and accurate camera calibration technique for 3D machine vision[EB/OL].[2009-12-20].http∶//research.microsoft.com/apps/pubs/default.aspx?id=66690.
[4]STEGER C,ULRICH M,WIEDEMANN C.Machine vision algorithms and applications[EB/OL].[2009-12-20].http∶//www.amazon.com/Machine-Vision-Algorithms-Applications-Carsten/dp/3527407340#noop.
[5]FITZGIBBON A,PILU M,FISHER R B.Direct least square fitting of ellipses[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1999,21(5):475-480.
