基于三次谐波电流注入的六相感应电动机仿真分析
2010-06-23王成元苏启明
王成元 苏启明 黄 伟
(沈阳工业大学电气工程学院,沈阳 110870)
1 引言
与三相电动机相比,多相电动机主要具有以下优点:
(1)磁势波形得到改善,影响较大的空间谐波次数增加,且幅值下降,转矩脉动的幅值减小,而脉动的频率增加,电动机的噪声变小,系统的动态特性得到改善。
(2)转子电流接近正弦,转子谐波损耗减少,效率提高。
(3)三相电动机是通过增加每相串联匝数,实现高压大容量,多相电动机则是通过增加电动机相数,实现低压大容量。故大容量的的多相电动机,额可以采用低压变频器,避免功率器件串联,特别适合无法得到高压,但需要输出大功率的场合。
(4)电动机冗余度高,多相电动机的一相或较少的几相定子绕组开路并不会影响驱动系统的起动和运行,只需减载运行而不必停机,适合高可靠性要求的领域。
集中整距六相感应电动机不仅具有上述优点,而且还有其独特的优势。
传统的感应电动机提高功率密度的方法是从电动机设计角度,通过优化电动机尺寸,减少电动机的极数来实现功率密度的提高,随着电动机设计技术的发展进入了一个新时代, 带动了评估与优化带有不同电流与反电势波形的各种结构类型电动机功率水平的方法的研究。本文利用谐波电流来产生有用的转矩,提高转矩密度。
谐波注入法可以实现谐波抑制,功率因数校正,无速度传感器感应电动机速度识别等等,本文通过谐波注入法注入三次谐波电流从而提高感应电动机的电磁转矩。由于三次谐波电流在中点连接的相数为3的倍数的电动机中会相互抵消,故目前的研究集中在五相感应电动机和六相双Y移30°绕组感应电动机,本文选用中点不连接的集中整距绕组的六相感应电动机。
本文从谐波磁动势入手,理论上定性的得出了六相感应电动机能够增加电动机的电磁转矩,并建立了考虑三次谐波电流和空间谐波相互作用产生转矩条件下的数学模型,该模型能真实反映电动机的物理实际。通过仿真分析,得到与理论相吻合的结论。
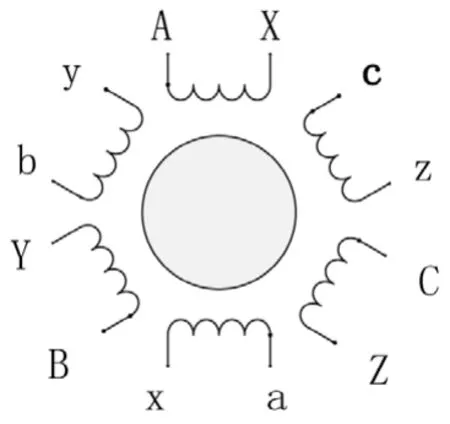
图1 星点不连接六相感应电动机
2 六相绕组谐波磁动势分析
用绕组函数和傅里叶分析是分析绕组谐波磁动势的有效方法。图为六相整距绕组的一相绕组函数图和120°导通电流波形。
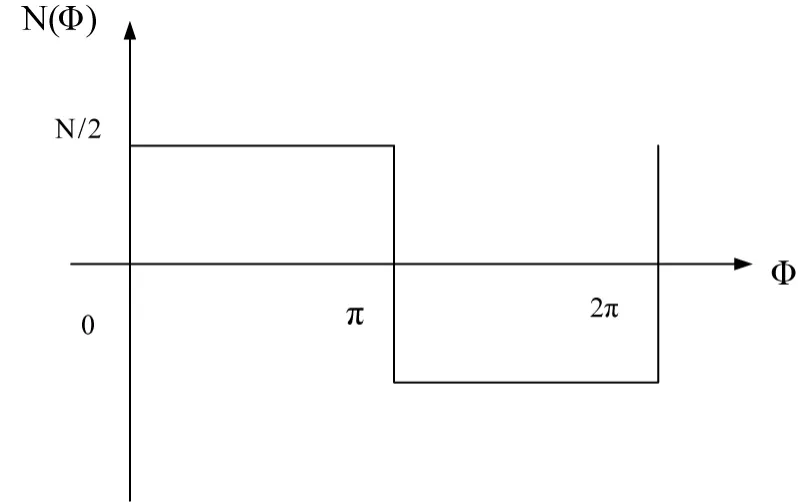
图2 绕组函数图
采用绕组函数的方法,n相对称绕组中第一相的绕组气隙磁势为

将绕组函数和绕组电流傅里叶级数展开,则气隙磁势用谐波形式表示为
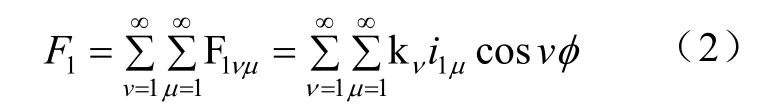
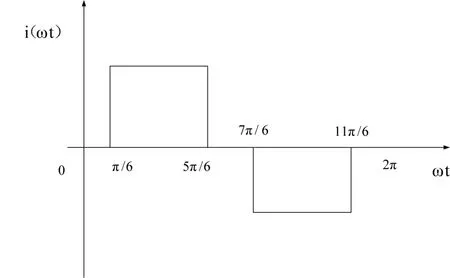
图3 绕组函数图
其中,V为空间谐波次数;U为时间谐波次数。同样地,其余相绕组磁势谐波可表示为
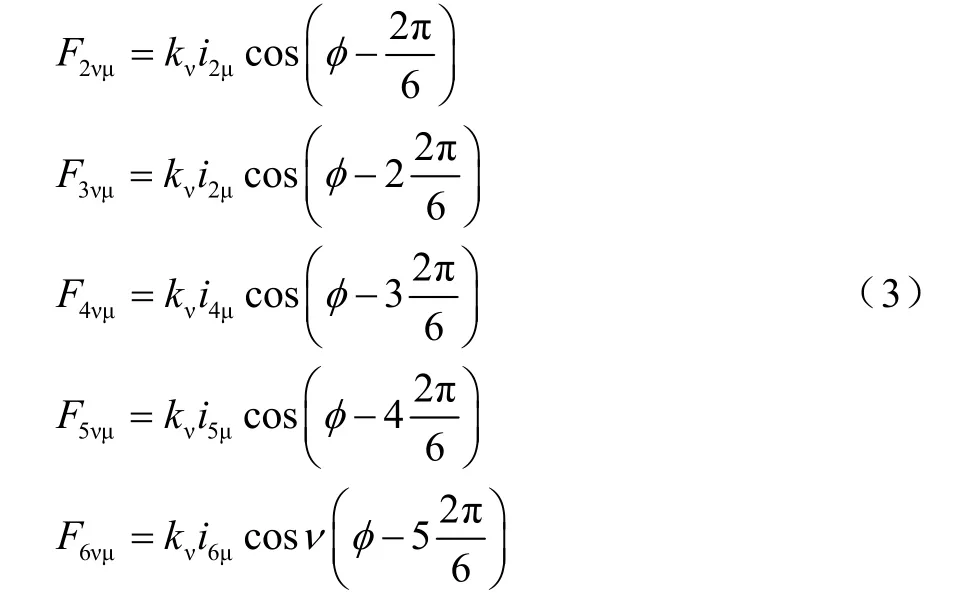
假设绕组电流为n相对称电流,则每相电流的各次谐波可表示为
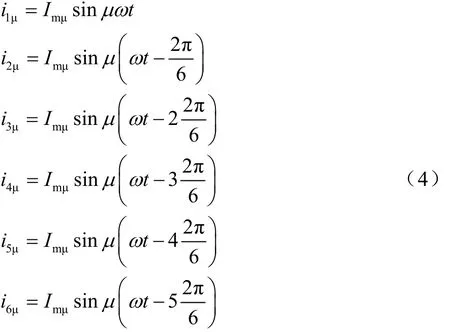
由于对称性,傅里叶级数展开的绕组函数为
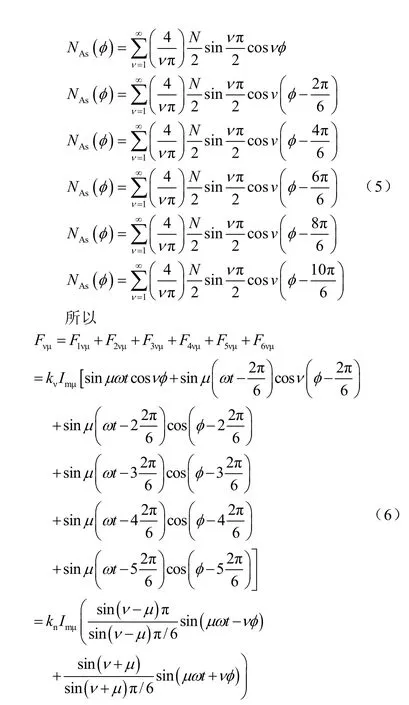
由此得出结论:①与三相绕组相比,低次谐波的影响减少,电机转矩脉动频率增加,幅值减少,转矩电流比略微增加;②于磁场为平定波,电机铁芯利用率提高,电机转矩密度增加。
3 考虑三次谐波的六相感应电动机数学模型
一般分布绕组六相感应电动机数学模型的建立是假设绕组为正弦分布,即除基波外绕组其他谐波分量都被忽略。那么绕组在考虑空间谐波的影响,所建立的模型显然有所不同。为了考虑三次谐波电流和三次空间谐波相互作用产生转矩,取定子电流及其微分为输入,转子电流为状态变量,在静止自然坐标系下:
(1)转子电压方程
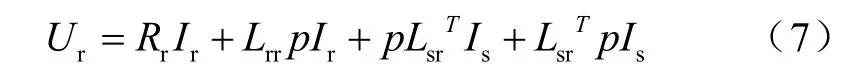
(2)定子电压方程
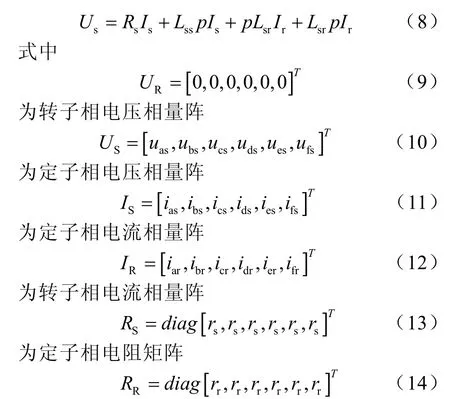
为转子相电阻矩阵。LSS,LRR为定转子电感矩阵,LSR为定子到转子互感矩阵,LSRT为LSR的转置,微分算子p=d/dt。设θr为以定子a相绕组轴线为参考时的转子位置电角度,则 LSR和 LSRT互感阵中的元素与θr有关。
(3)转子运动方程
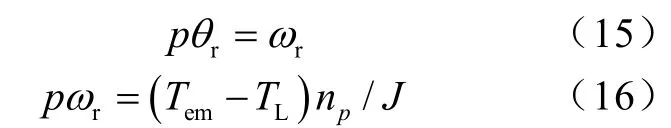
式(16)中Tem、TL、np、J分别为电磁转矩、负载转矩、极对数和电机转动惯量。
将式(15)带入式(7)整理得

式(15)、(16)、(17)即为电机状态方程。
(5)电感矩阵的求取
参考绕组函数中的式(5),只考虑基波和三次谐波,a相绕组可以表示为

同理,其他电感也可求得。
4 仿真分析
基于以上数学模型,在Matlab/Simulink软件平台下,通过编制S函数和搭建模块实现电动机的建模,参数通过封装,界面式输入。
利用该模型对一台六相 4极电动机进行了仿真,电动机参数见表1。
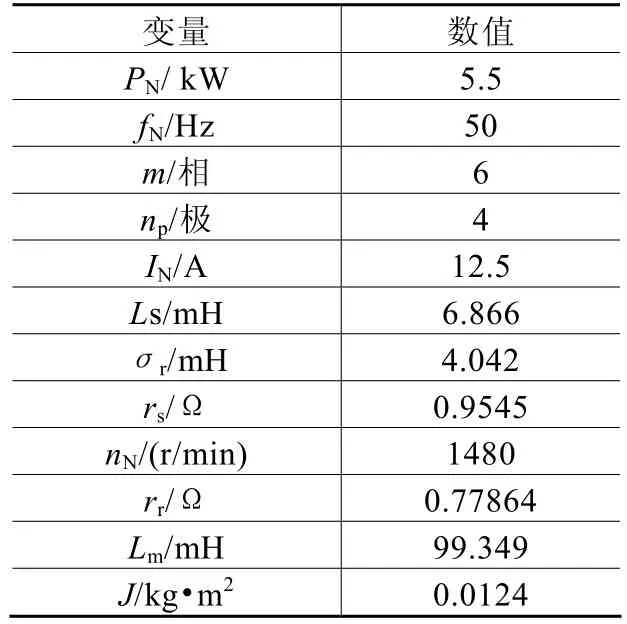
表1 电动机参数
电动机参数一致即整个铜损也一样的情况下,分别做出了加入三次谐波电流和不加入三次谐波电流情况下的仿真曲线,限于篇幅只给出了转速和电磁转矩波形,由仿真结果得出如下结果:
(1)由转速波形看出,在保证相同的惯量等条件下,加入可三次谐波电流的速度响应比没有加入的要快,表明有用谐波转矩产生。
(2)由转矩波形可以看出,在启动和图加负载时段,三次谐波电流产生的瞬时最大转矩也比没有加入三次谐波电流的要大。
(3)仿真过程中还发现,如果数学模型电感阵中没有谐波项,即使加入三次谐波电流,对转矩和转速波形几乎没有影响,因为只有三次空间谐波和三次时间按谐波才能户型啊作用产生有用的转矩,三次谐波电流与空间基波相互正交,不产生转矩,验证了在考虑加入三次谐波电流时的数学模型,电感阵必须发生变化。
所以由于采用时开环仿真,没有考虑控制因素。虽然提高转矩效果并不明显,但能定性看出确有提高。
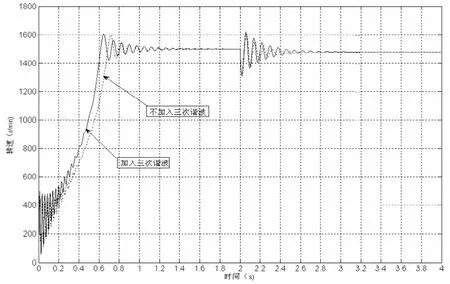
图4 速度波形对比
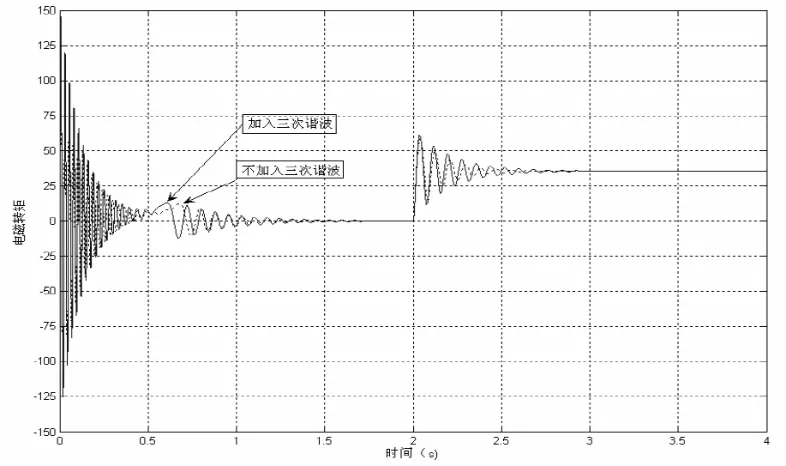
图5 转矩波形对比
5 结论
本文建立了六相感应电动机考虑三次谐波电流条件下的数学模型。并通过编制S函数实现了电动机的建模,该模型通用性好,仿真表明六相感应电动机中加入三次谐波电流可以改善磁势的空间分布,解决感应电动机中铁心材料的局部饱和问题,从而增强了铁心材料的利用率,增加转矩,提高转矩密度。同时表明所建模型正确,对进一步研究电流型逆变器方波供电的仿真分析有一定的参考价值。
[1]侯立军,苏彦民. 陈林等. 多相感应电机调速系统的发展现状和应用前景[J]. 微电机, 2001(5) ∶ 43 - 44.
[2]吴新振, 王祥珩, 罗成. 多相异步电机谐波电流与谐波磁势的对应关系[J]. 清华大学学报(自然科学版),2005,45(7)∶865-868.
[3]陈林,熊有伦. 多相感应电动机调速系统研究与应用[J].微特电机,2002(1)∶33-35.
[4]H.A. Toliyat. Analysis of a Concentrated Winding Induction Machine for Adjustable Speed Drive Applications Part1 (motor analysis) [J]. IEEE trans. On Energy Conversion,1991,6(4).
[5]M.J. Duran. Harmonic CurrentInjection inMulti-phase Machines for High Specific Torque Including SkinEffect [J]. IEEE Transact ion on Energy Conversion,1994,8(3).
[6]H.A. Toliyat. Analysis and Simulation of Five-phase Synchronous Reluctance Machines Including Third Harmonic of Airgap MMF [J]. IEEE trans.on Industry Applications,1998,34(2).
[7]A.R.Munoz and T.A.Lipo, “Dual stator winding induction machine drive,” [J]IEEE transactions on Industry Applications, 2000,36(9)∶1369-1379.
[8]Renato de Oliverira da Costa Lyra .Torque Density Improvement in a Six-Phase Induction Motor with Third Harmonic Current Injection [D].University of Wisconsin- Madison.2002.
