基于s函数的异步电动机任意参考系建模和仿真
2010-06-22杨军
杨 军
(西南交通大学电气学院,成都 610031)
1 引言
三相交流异步电动机的数学模型是一个高阶、非线性、强耦合的多变量系统,不能像直流电动机那样对转速和磁链进行高性能控制。通过对电动机数学模型的坐标变换可以实现其解耦。本文利用Matlab/Simulink中的 S-Function函数对任意坐标系下的异步交流电动机进行建模,并给出仿真结果。
2 异步电动机的数学模型[1]
在建立交流电动机的运动方程时,为便于分析,常常假设电动机为“理想电动机”。理想电动机的基本假设如下[2]:
(1)忽略空间谐波。
(2)忽略定、转子铁心的磁饱和。
(3)忽略铁损。
(4)忽略频率和温度对于电阻的影响。
规定各绕组电压、电流、磁链的正方向符合电动机惯例和右手螺旋定则,则有:
(1)电压方程

(2)磁链方程
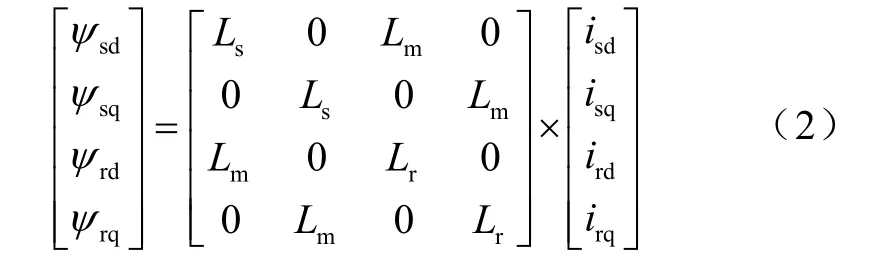
(3)电磁转矩
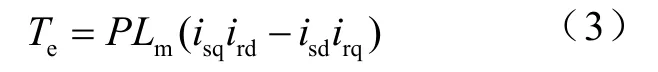
(4)运动方程

式中,下标d、q分别表示d轴和q轴分量;下标s、r表示定转子;ω是转子旋转电角速度;ω1是参考坐标系旋转速度;Te、TL分别为电磁转矩、负载转矩;Ls、Lr、Lm分别为定子电感、转子电感和定转子互感;P为电动机极对数;J为电动机的转动惯量。
当ω1=0时,此为αβ静止坐标系;当ω1=ω时,此为转子速 dq坐标系;ω1=2πf1时,此为同步速坐标系。由此可见,此模型与单独的 αβ坐标系、dq坐标系、同步坐标系电动机模型相比有很大的优势,既可以避免重复建模,还可以观察不同参考坐标系下各个物理量的不同形式。
3 电动机建模
电动机模型求解一般有三种方法:①基于数值计算方法求解微分方程。对于复杂系统,状态方程计算以及某些环节中的求导运算都会引来误差,甚至数值不稳定;②基于Matlab/Simulink基本元件搭建电动机仿真模型。此方法方便和快捷性,但繁杂,易出错;③基于Simulink中的s函数(System Function)建模,可以使问题求解更方便快捷,仿真精度也高。我们以笼型异步电动机为例,介绍 s函数在电动机仿真中的应用。
(1)电动机的状态方程[2]
取状态变量:isd、isq、ird、irq、ω、θ;输入变量:usa、usb、usc、ω1;则电动机的状态方程可写为

(2)电动机模型的s函数描述[3]
根据上面的状态方程,我们就可以编写电动机的s函数ac_motor.m。用s函数建模关键要清楚选择的状态变量和输入量,要理清它们之间的关系;s函数的电动机模型简单明了,不易出错。在此仅给出连续状态计算阶段的代码:


(3)电动机系统模型
电动机仿真系统的模型如图1所示。双击其中的S-Function模块,在对话框中的S-function name栏目内填写 ac_motor,就可以建立起该模块和ac_motor.m文件之间的联系。

图1 电动机系统模型
4 仿真实验
使用上述模型,对笼型异步电动机进行仿真。电动机参数:Pn=37kW,Un=380V,fn=50Hz,nn=1480r/min,Tn=238.7N/m,Rs=0.08233Ω,Rr=0.0503Ω,Ls=0.041389H,Lr=0.041389H,Lm=0.040665H,J=0.37N/m2,P=2。
设定仿真时长为3s。仿真算法为ode(45)变步长算法,最大步长1e-4。0s-1s时ω1=0,1s-2s时ω1=ω,2s-3s时ω1=2πf1。由此来观察参考坐标系变化了之后电动机电气量和机械量的改变。电动机带额定负载起动。
由图 1、图 2可以看出,电动机的起动时间大约是0.6s左右,电动机起动完成后就保持稳定运行,和参考坐标系的变化没有关系。其中实际转速1486r/min比额定转速1480r/min稍高是因为模型忽略了铁损和机械损耗等因素的影响。
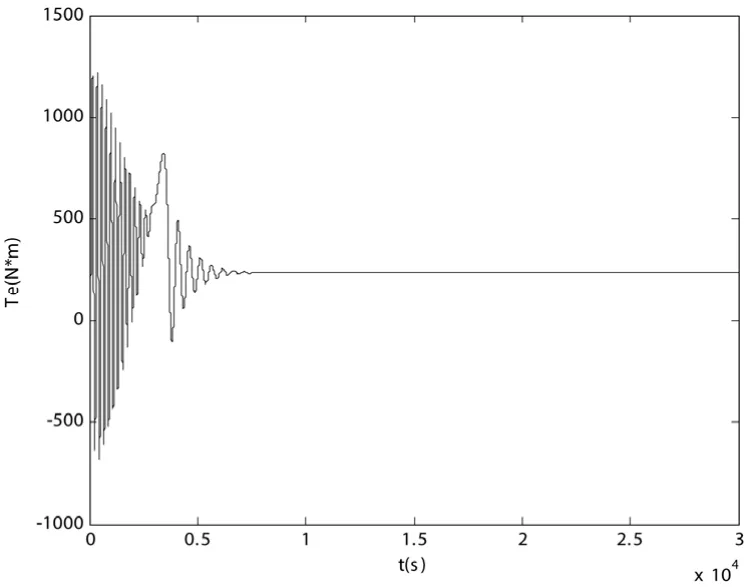
图2 电磁转矩波形

图3 转子转速波形
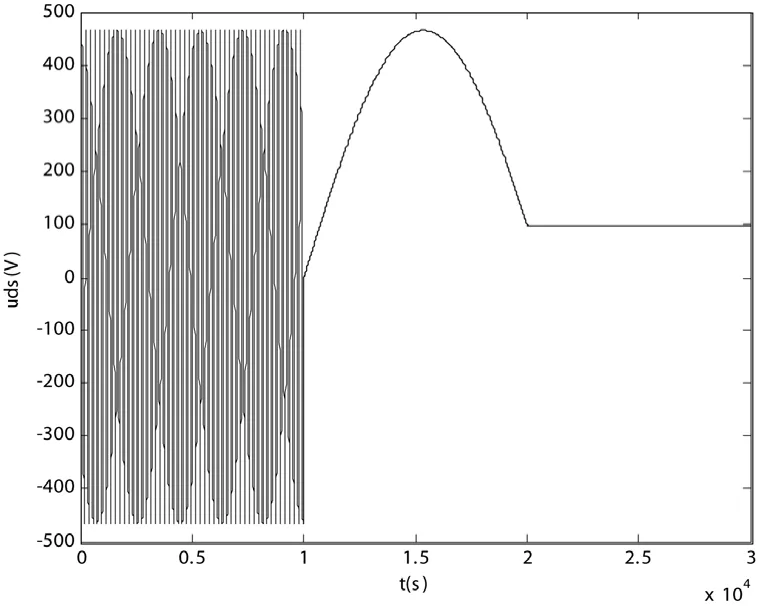
图4 定子d轴电压波形

图5 定子d轴电流波形

图6 转子d轴电流波形
由图3、图4和图5可以看出:
(1)ω1=0,在静止坐标系下电压和电流变量仍是交变的。由于电感矩阵的时变因素得以消除,故仿真速度较快。
(2)ω1=ω,参照系的旋转速度是通过实时检测电动机的转速 ω获得的。在dq坐标系下,电压和电流变量虽任然是交变的,但波动的频率比静止坐标系小。
(3)ω1=2πf1,在同步坐标系下,电压和电流变量完全变成了直流分量。
这表明不同坐标系下对电动机特性进行分析时,只对分析过程的繁简和电量的表达形式有影响,不影响电动机的机械分量。
5 结论
本文从异步电动机任意坐标系模型出发,用Matlab/Simulink 环境下s函数构造了异步电动机的动态数学模型,以实际电动机为例,对其进行了仿真研究,验证了该仿真模型的正确性。该模型结构简单,易仿真,精度高,对于理解不同参考系下的电动机电量变化有积极的参考价值,可以在实际工程设计中应用。
[1]贺昱曜.运动控制系统[M].西安:西安电子科技大学,2009.
[2]汤蕴璆.交流电动机动态分析[M].北京:机械工业出版社,2005.
[3]薛定宇,陈阳泉.基于 Matlab/Simulink的系统仿真技术与应用[M].北京:清华大学出版社,2002.
