渗流潜蚀作用临界发生条件的推导
2010-06-21李喜安陈文军邓亚虹贾丽娜
李喜安,陈文军,邓亚虹,李 亮,贾丽娜
(长安大学,西安 710054)
潜蚀作用的分布极为广泛,几乎所有的气候条件、有机土壤和矿物质土中,在扰动和农耕地中,在某些松散的沉积物和基岩中,甚至于某些可溶性基岩中均可发生潜蚀作用。早在1886年Von Richthofen研究黄土地貌时就曾注意到黄土地层中的潜蚀现象[1],此后,许多地质学、地貌学、气候学、地理学、水土保持等领域的诸多学者在进行研究工作的过程中,有意无意地对世界各地的潜蚀现象都有所提及[2-5]。1963年Parker首次较为系统地报道了潜蚀现象,指出了地下径流侵蚀对地貌塑造和土壤侵蚀的重要性[6]。随后Parker和Jenne在1967年、Bell在1968年、Heede在1971年都相继报道了美国干旱地区的潜蚀现象[7],1980年Gilman和Newson[8],1981年Jones[9]报道了在大不列颠湿润地区的潜蚀现象。1982年一些研究报告报道了在Bryan和Yair干旱半干旱地区的潜蚀作用[10]。20世纪60年代至70年代,关于盆地产流复杂性的证据越来越多,而这一时期有关地下径流对暴雨水力学特性响应的证据也开始出现,与此同时在不同气候区不同土壤类型中有关潜蚀特征的报道也越来越多,这些研究引起了关于潜蚀重要性的越来越多的讨论。
国内关于地下潜蚀方面的研究多集中于黄土洞穴侵蚀的成因上,其观点主要有机械侵蚀说、溶蚀说、多因素综合成因说等三种[11]。国外目前的文献则多集中于地下径流和潜蚀过程及其与潮湿高沼地水力学过程的关系、荒地地貌的关系、与半干旱地区土壤侵蚀关系的研究。国内外关于潜蚀作用发生机理的研究也时有出现,但大多浅尝辄止,尤其涉及到潜蚀作用激发条件方面的文献极为缺乏,这一现状在一定程度上对潜蚀相关的研究构成了约束。鉴于此,本文在对“管涌”、“渗透压密”、“流土”、“突涌”等几种最为常见的渗流潜蚀作用概念模型严格界定的基础上,利用解析方法推导了潜蚀作用的发生条件,为潜蚀作用的进一步研究提供了理论基础。
1 管涌、渗透压密及其临界发生条件
管涌是指在任意方向渗透水流作用下,在砂或砂质土层内部空腔或外部的渗流出口处,细颗粒在粗颗粒形成的孔隙通道中集中移动、流失,或伴随着细颗粒的流失粗颗粒也继而流失,从而形成管状侵蚀通道的现象。管涌根据其侵蚀结果可分为有害管涌和无害管涌两种形式。有害管涌(harmful piping)指在渗透水流作用下,土中的细颗粒在粗颗粒形成的孔隙中移动,以至流失,随着土的孔隙不断扩大,渗透速度不断增加,较粗的颗粒也相继被水流逐渐带走,最终导致土体内形成贯通的径流管道,其发展破坏过程需要有一定的时间,是一种渐进性质的破坏。无害管涌(unharmful piping)发生时,细颗粒被带走,但粗颗粒形成的骨架尚能支持,虽然此时渗流量和渗流速度增大,但粗颗粒骨架并不发生破坏(图1)。

图1 无害管涌作用概念模型
若以单个土壤颗粒为研究对象,则渗透力是由于渗流的运动而对土颗粒表面产生的法向力和切向力等外力的合力。由图2可以显示出,在任意方向的渗流作用下,细颗粒在土体内发生移动,但由于渗透边界条件限制而不流失于土体外,饱和土体在渗透力作用下会发生的体积缩小现象,正如松散堆积体在自重作用下产生自重压密一样,这种在渗透力作用下发生的土体整体或局部体积缩小现象现象称为渗透压密,渗透压密后压密部位的孔隙吼道普遍减小往往造成渗流量减小。

图2 渗透压密作用概念模型
渗透压密和无害管涌只是土层所处的渗透边界条件不同,其细颗粒的启动条件一致。由于该过程不是土体的整体运动,因此不能对土体整体进行受力分析,但若用横截面毛管模型表示骨架孔隙[12],则可取单个可动细颗粒及其赋存的圆管空间作为研究对象,对可动细颗粒进行受力分析。假定可动细颗粒周围是由骨架颗粒围成的微型圆管,以自下而上的渗流为例(图3),忽略双电场力的影响,则细颗粒受到的力有渗流对其向上的拖曳力、细颗粒的水下重力和细颗粒与孔隙壁之间的粘聚力。
根据Happel的推导结果,当渗流方向向上时,细颗粒受到渗流向上的拖曳力为F=6πμr[v0(1-b2/B2)],其中r为细颗粒半径,b为细颗粒中心到微型圆管轴线的垂直距离,B为微型圆管的半径,μ为颗粒-流体系统的表观粘滞系数。
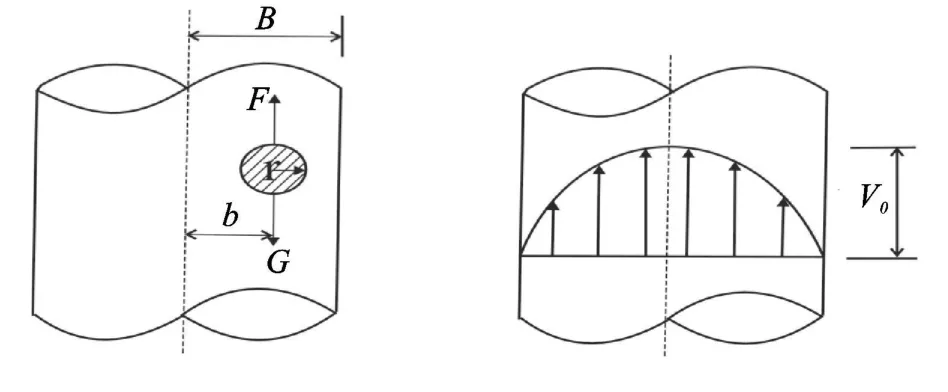
图3 横截面毛管模型[12]

将上述各式代入(1)式得到细颗粒的启动条件为
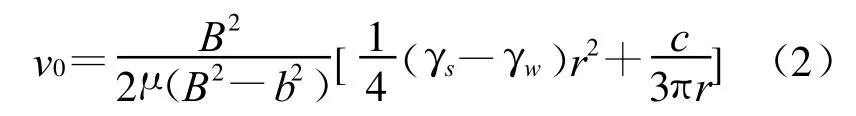
当细颗粒贴壁时,b=B-r,代入(2)式得:
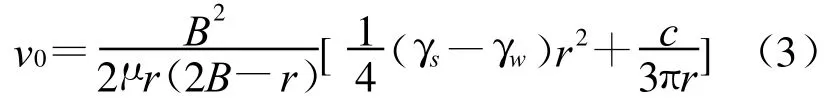
即对于r一定的贴壁细颗粒,其临界启动渗流速度只和渗流的表观粘滞系数μ、孔隙截面半径B以及土壤的粘聚力c有关。此时细颗粒的启动须克服其自身的重力和细颗粒与孔隙壁之间的粘聚力。
对于水平渗流,细颗粒和管壁之间以粘聚力c胶结时(假定胶结接触的面积为s),细颗粒的启动则只需克服细颗粒与管壁胶结处的抗剪强度τ=σn◦tgφ+c,其中为细颗粒与管壁胶结物的内摩擦角。此时处于临界启动状态的细颗粒,其极限平衡条件为F=τ,即:
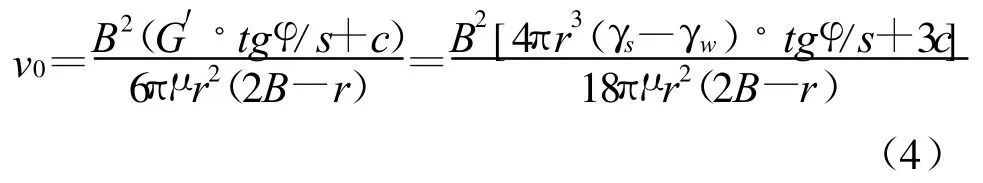
若细颗粒和管壁之间无任何胶结,则c=0,那么只需克服细颗粒与管壁之间的静摩擦力f=G′◦tgφ′,此时处于临界启动状态的细颗粒,其极限平衡条件为F=f=G′◦tgφ′。φ′为细颗粒在松散堆积状态时的内摩擦角,即:
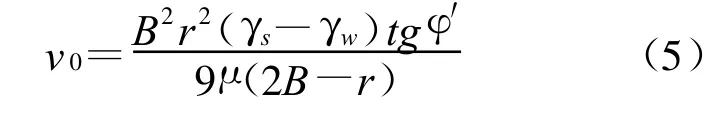
而对于垂直向下的渗流,处于临界启动状态的细颗粒和管壁之间以粘聚力c胶结,其极限平衡条件为:G′+F=σn◦tgφ+c=c(此时 σn=0),则有:
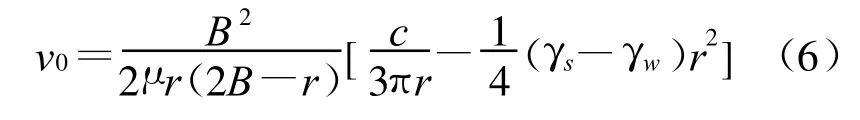
有害管涌中可动细颗粒的启动条件与无害管涌相同,不同的是无害管涌中粗颗粒胶结强度较高或渗流力较小,因此粗颗粒能够形成稳定支架而不至于破坏,但有害管涌中可能由于粗颗粒胶结强度不够或渗流力较大而能够使得粗颗粒启动从而发生破坏。有害管涌中可动粗颗粒的启动条件同样可借鉴可动细颗粒的启动条件分析方法进行,此不赘述。
2 流土发生的临界条件
流土是在任意方向渗透力作用下,饱和土体中局部土体中所有颗粒同时整体起动而发生鼓胀、移动或流失的现象。根据渗流方向的不同,流土可分为底部流土(一般意义上的流土)、顶部流土、侧向流土和斜向流土,图4为底部流土发生机理示意图。
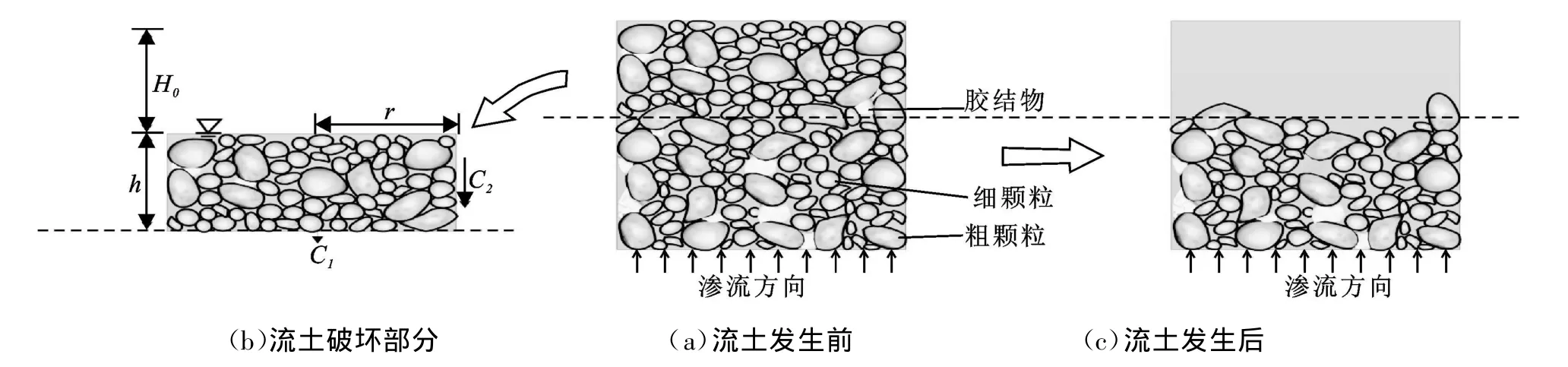
图4 底部流土发生机理示意图
对于底部流土,由于是土体或土颗粒的整体同时运动,因此应取整体运动的那部分圆柱状饱和土体(设高为h,半径为r,饱和土的粘聚力为c,浮重度为γ′=γsat-γw,超压水头为H0)为研究对象,则其所受到的力有作用在圆柱体底面的水压力(P=πr2H0γw)、圆柱土体的浮重(G″=hπr2γ′)、圆柱土体侧面及底面粘聚力的合力(C=2πrhc)(二元结构土层,因为近地表,所以可设土体侧面上的正压力σn=0,又由于分界面是不同渗透性土层的岩性界面,所以圆柱土体底面粘聚力的合力忽略不计),根据饱和圆柱土体受力平衡条件G″+C=P,可得二元结构地层上层发生流土的临界水头差为
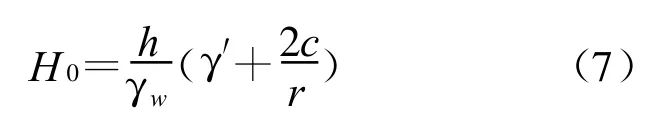
若流土在同一土层中发生,则圆柱土体侧面及底面粘聚力的合力C=πrc(2h+r),同样可根据极限平衡条件得到同一土层中发生流土的临界水头差:
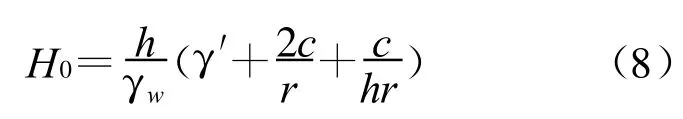
对于二元地层结构地层为了防止流土,一般采用砂砾石压重,此时若要发生流土,则要满足G″+G″1+C=P(砂砾石压重为G″1,设γ′为砂砾石重度,hy为砂砾石层的厚度,粘聚力为0),则相应的临界水头为
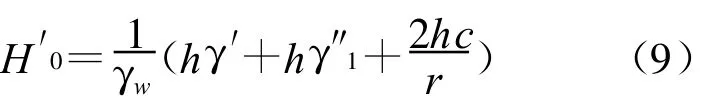
对于顶部流土,同样是局部土体的整体运动,同理取该部分圆柱状饱和土体为研究对象(设其高为h,半径为r,饱和土的粘聚力为c,饱和重度为 γsat,超压水头为H0),则发生顶部流土的土体处于极限平衡状态时所受到的力有土体的饱和重力(G=hγsat)、圆柱体底面所受到的水压力(P=πr2H0γw)、圆柱体侧面粘聚力的合力(C=2πrhc)(二元结构地层),根据饱和圆柱土体受力平衡条件C=G+P,可得顶部流土发生的临界水头为
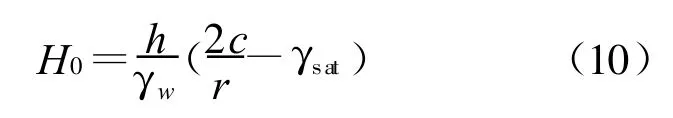
同理可得同一土层顶部流土发生的临界水头:
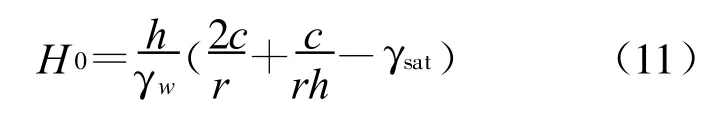
对于侧向流土,取水平方向对整体移动部分圆柱土体进行静力平衡分析,此时圆柱土体在水平方向所受的力主要有圆柱体底面所受到的水压力P=πr2γw(H0+r)、圆柱体侧面粘聚力的合力(C=2πrhc)(二元结构地层),根据饱和圆柱土体受力平衡条件C=P,可得侧向流土发生的临界水力坡降为:
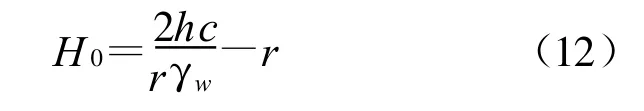
同理可得同一土层侧向流土发生的临界水头:
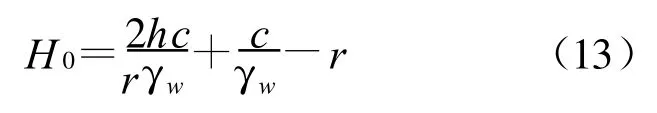
3 突涌及其发生的临界条件
由流土的定义可见,发生破坏的土体是饱和的,因此在受力分析时采用的是饱和容重。实际情况中还存在其他两种基本渗流情况:①土体的破坏水头可能比有稳定渗流时产生的水头小(即土体强度小于渗透力),这样一旦土层中产生渗流就会使土体发生破坏(破坏部分土体非饱和);②超过土体破坏强度的渗流力是突然施加的,破坏的那部分土体中还来不及产生渗流就发生了破坏(破坏的那部分土体是非饱和的)。这两种渗流作用方式下虽然也是局部土颗粒整体起动破坏,但发生破坏的那部分土体在破坏的瞬间是非饱和的,由于后面分析其力学机理时采用的容重不一样(应采用天然容重而不是饱和容重),因此应予以区别。为了突出渗流作用方式的特点,可将其称作“突涌”[13](soil-burst),根据渗流方向的不同,同样可分为顶突、底突、侧突和斜突。
对于底突,取同时移动圆柱状非饱和土体单元(设其高为h,半径为r,非饱和土的粘聚力为c′,饱和土的粘聚力为c,非饱和重度为γ,超压水头为H0)为研究对象,则其所受的力有作用在圆柱体底面的渗透压力[P=πr2(H0+h)γw]、非饱和圆柱土体的重力(G=hπr2γ)、圆柱土体侧面的粘聚力(C′=2πrhc′)(二元结构地层),根据非饱和圆柱土体受力平衡条件G+C′=P,可得底突发生的临界水力坡降为
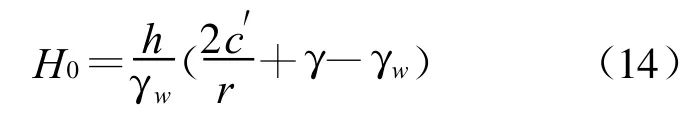
同理可得同一地层发生底突的临界水力坡降为
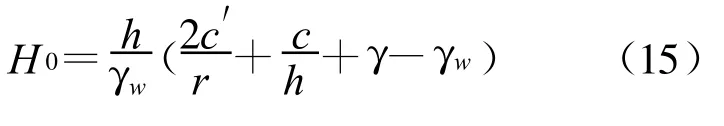
对于顶突,同样取同时移动圆柱状非饱和土体单元为研究对象,则其所受的力有作用在圆柱体底面的渗透压力(P′=πr2H0γw)、非饱和圆柱土体的重力(G=hπr2γ)、圆柱土体侧面的粘聚力(C′=2πrhc′)(二元结构地层),根据非饱和圆柱土体受力平衡条件C′=G+P′,可得顶突发生的临界水力坡降为
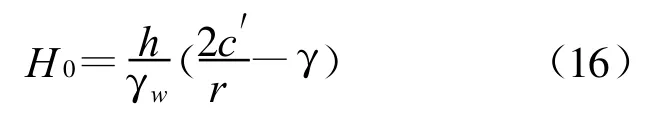
同理可得同一地层发生顶突的临界水力坡降为
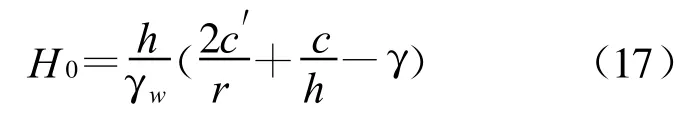
对于侧突,取水平方向对整体移动部分圆柱土体进行静力平衡分析,此时其在水平方向所受的力主要有圆柱体底面所受到的渗透压力[P″=πr2γw(H0+r)]、圆柱体侧面粘聚力的合力(C′=2πrhc′),根据饱和圆柱土体受力平衡条件C′=P″,可得侧突发生的临界水力坡降为
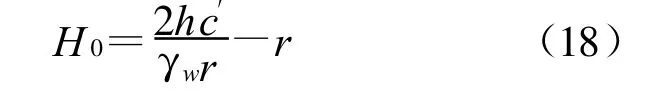
同理可得同一地层发生侧突的临界水力坡降为
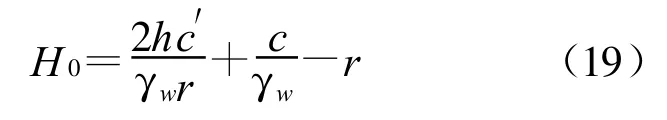
4 地下径流作用下的潜蚀
在地下径流冲刷作用下发生的机械潜蚀称作地下冲蚀或地下冲刷侵蚀(underground scour),地下冲蚀过程需要一定临空空间或自由空间,因而地表径流对地表以下的土层进行冲蚀的前提是地层中必须存在径流通道。实际上这样的径流通道是存在的,它们往往是土层中的各种节理裂隙(尤其是构造节理、垂直节理、湿陷裂隙、卸荷裂隙等等)或动植物孔洞,或地下各种强渗通道经过渗流的作用而在三维空间贯通所形成的各种地质缺陷[14]。水的冲蚀作用通常以冲淘、切割、涮窝拉槽、溅蚀等形式进行侵蚀,由于不属于渗流侵蚀的范畴,且已有许多研究成果,因此本文暂不讨论。
5 结语
本文在对“管涌”、“渗透压密”、“流土”、“突涌”等几种最为常见的渗流潜蚀作用概念模型严格界定的基础上,利用解析方法推导了潜蚀作用的发生条件,为潜蚀作用的进一步研究提供了理论基础。应该指出的是,渗流潜蚀作用发生的环境往往复杂,其环境的多样性反映了各种形式的渗流潜蚀作用起始过程的多样性,从而决定了渗流潜蚀作用具有继发性、动态性和复杂性等特征,这一事实也表明了对于渗流潜蚀作用发生临界条件的判断应就其具体受力情况来具体分析,而要建立一个普遍适用的渗流潜蚀发生模型则是不现实的。
[1]Von Richthofen F.Führer Forschungsreisende.Aiileitung zu Beobachturigen ü ber Gegenstände der physischen Geographie and Geologie[M].Berlin:Oppeenheim,1886:308-310.
[2]Van Zyl D,Harr M E.Seepage erosion analyses of structures[C].Proc.,10th Int.Conf.On Soil Mech.And Found.Engrg.,Sweden:Stockholm,1981:530-509.
[3]Lane E W.Security from underseepage:Masonary dams on earth foundations[J].Trans.Am.Soc.Civ.Eng.,1935:1235-1272.
[4]Terzaghi K.Der Grundbruch an Stauwerken und seine Verhuetung[J].Die Wasserkraft,1922,17:445-449.
[5]Khilar K C,Folger H S,Gray D H.Model for pipingplugging in earthen structures[J].J.Geotech.Eng.,1985,111(7):833-846.
[6]Parker G G.Piping,a geomorphic agent in landform development of the drylands[J].IAHS Publ.,1963,65:103-113.
[7]Parker G G,Jenne E A.Structural failure of western higways[J].Highway Research Record,1967,203:57-76.
[8]Gilman K,Newson M D.Soil Pipes and Pipeflow:A Hydrological Study in Upland Wales[M].Geobooks,Norwich,1980.
[9]Jones J A A.The Nature of Soil Piping:a Review of Research[M].BGRG Research Monograph Series No.3.Norwich:Geo Books,1981.
[10]Harvey A.The role of piping in the development of badlands and gully systems in south-east Spain[C]//Bryan R B,Yair A.Badland Geomorphology and Piping.Geobooks,Norwich,1982:317-335.
[11]李喜安.黄土暗穴的成因及其公路工程灾害效应研究[D].西安:长安大学,2004.
[12]刘忠玉,乐金朝,苗天德.无粘性土中管涌的毛管模型及其应用[J].岩石力学与工程学报,2004,23(22):3871-3876.
[13]李广信,周晓杰.土的渗透破坏及其工程问题[J].工程勘察,2004(5):10-14.
[14]李喜安,彭建兵,郑书彦.湿陷性黄土地区土壤洞穴侵蚀模式研究[J].水土保持研究,2005,12(6):25-27,97.
