基于改进自由搜索算法的电力经济负荷分配

夏 澍，张建华，邱 威，葛晓琳

（华北电力大学电气与电子工程学院，北京102206）

基于改进自由搜索算法的电力经济负荷分配

夏 澍，张建华，邱 威，葛晓琳

（华北电力大学电气与电子工程学院，北京102206）

0 引言

经济负荷分配（ELD）是电力系统运行控制中重要的优化问题，其优化目标是在一个电厂内或电力系统内合理分配各机组负荷，使得在满足负荷和运行约束的条件下发电成本最小[1]。由于火电机组众多，机组耗量特性与阀点效应复杂，导致ELD是一个高维、非线性、不可导、多约束问题，不易解决。经典的数学方法，如线性规划法、拉格朗日松弛法、动态规划法等方法在解决此类问题时存在严重的不足[2-4]。近年来，随着智能优化算法的飞速发展，为解决非线性问题提供了一条新的道路。很多学者将遗传（GA）、粒子群（PSO）、人工免疫（AIA）、微分进化（DE）等算法应用到ELD中并在一定的程度上取得了较好的结果[5-8]。

自由搜索（FS）是由Penev和Littlefair在2004年提出的一种高效率智能优化算法[9]。该算法借鉴动物个体存在不同的嗅觉、机动性等特征，提出了个体灵敏度和邻域搜索半径的概念，并利用动物释放信息素的机理，通过信息素和灵敏度的比较确定各自新的寻优位置，经过不断的搜索找到最优解。FS算法与GA、PSO、ACO等算法相比，在兼顾局部搜索和全局搜索，提高鲁棒性和自适应等方面都有了很大的提高[10]。但是基本FS算法对搜索半径、信息素、灵敏度依赖性较强，若参数设置不当会导致搜索效率低、陷入局部最优等问题。本文针对这些缺点，调整了个体信息素和灵敏度的产生方式，采取了实时控制搜索半径方案，并以实际算例验证了该算法的寻优性能。

1 电力经济负荷分配的数学模型

1.1 目标函数

ELD问题的优化目的是在满足系统运行约束条件下，优化发电机组的出力，从而使系统的总发电成本最低，其目标函数如下：

式中，F为系统总发电成本；Fi（PGi）为第i台发电机的耗量特性；EVi为阀点效应引起的耗量特性变化；Ng为系统内发电机总数；ai、bi、ci、gi和hi为第i台发电机耗量曲线系数；PGi和PGimin分别为第i台发电机有功功率和有功功率下限。

1.2 约束条件

1）发电机运行约束条件：

式中，PGi、PGimin、PGimax分别为第i台发电机有功出力及其上下限。

2）机组出力爬坡约束：

式中，UGi、DGi分别为第i台发电机在相邻时段出力允许的最大上升和下降值。

3）电力平衡约束条件：

式中，PLD、PS分别为系统总负荷和系统总网损。系统网损可采用B系数法或潮流计算方法计算，若网损由B系数法计算，则网损与发电机有功功率的关系为：

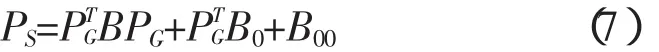
式中，PG为Ng维发电机有功功率向量；B、B0、B00为网损系数；B为Ng×Ng维对称方阵，B0为Ng维向量，B00为常数。

2 改进自由搜索算法

2.1 基本FS算法

2.1.1 初始化

同GA、PSO等进化算法一样，FS操作是针对一个由很多个体即候选解组成的种群。设初始种群S={X1，X2, …，XN},Xi∈Rn，第i个个体Xi=（x0i1,x0i2, …,x0in），其中n为优化问题解空间维数。一般个体向量Xi的各个分量按下式产生：

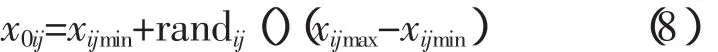
式中，xijmin、xijmax分别为第i个体第j个分量的上限和下限。

2.1.2 搜索过程

为了寻求较优的位置，每代个体各个分量需要在其邻域内进行搜索，其行为描述如下：

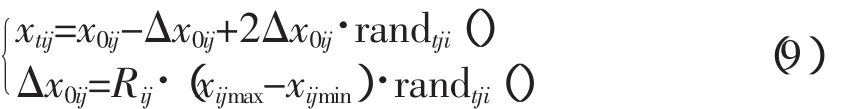
式中，randtij（）为[0,1]间的随机数；Rij为第i个个体第j个分量在搜索邻域的搜索半径，一般取[0,1]之间的数；t是搜索步中的当前小步数（t=1,2,…,T）；T是搜索步数。

2.1.3 择优过程

搜索过程中，对目标函数的符号做如下的规定：

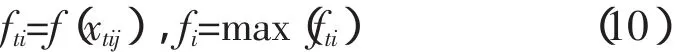
式中，fti是一个个体完成搜索步后的目标函数值。信息素定义为：

灵敏度定义如下：

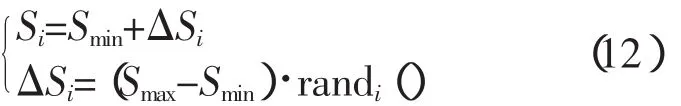
式中，Smin、Smax分别为灵敏度的最小值和最大值，Smin=Pmin，Smax=Pmax，Pmin、Pmax分别为信息素的最大值和最小值。

在一轮搜索结束后个体按下式选择新的位置，即下一次搜索的起始点。

2.2 FS算法的改进形式

2.2.1 信息素调整

标准FS算法是求解最大值问题，而本文的优化目标为最小值，若利用取对数或取负数的方式求解会影响信息素的产生，从而影响整个寻优过程。 因此本文利用式 （14）、（15）更新式（10）、（11），通过修改信息素的产生达到求解最小目标函数的目的。

2.2.2 灵敏度调整

灵敏度Si是FS算法中的另一重要参数，适当减少灵敏度，个体在邻域搜索的随机性增加，有助于提高搜索能力[11]，因此将式（12）按下式进行更新：

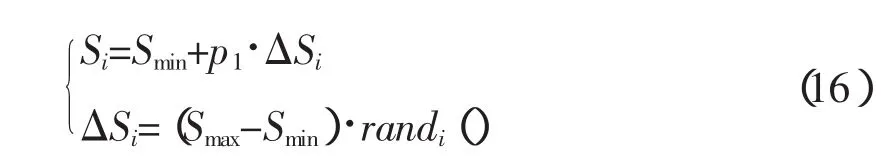
式中，P1为收缩系数（0.95≤P1≤0.99）。

2.2.3 搜索半径的自适应调节

搜索半径Rij是FS算法中的一个重要参数，其大小决定了寻优的性能。若Rij设置较大，则收敛速度明显降低；若Rij设置较小，则容易收敛到局部最优。迄今为止，一般都以进化代数作为参数对其进行动态调整[12]，但是这样做很难选取搜索半径的最小值，因此本文采取了一种方案，首先运用进化代数作为参数对其进行动态调整，当Rij比较小时，利用最优位置与当前个体位置间的距离进行调整，具体实现如下：

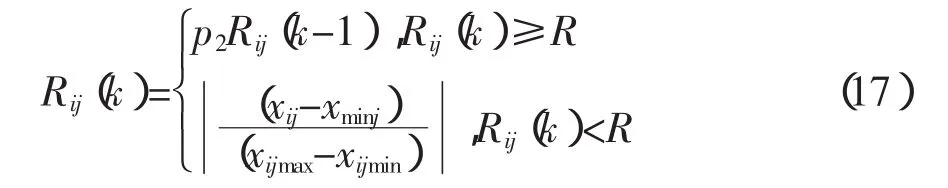
式中，k是当前代数；p2为收缩系数（0＜p2≤1）；xij为第i个个体、第j个分量；xminj为当前最优位置第j个分量；R为搜索半径分界值（0＜R＜1）。

3 算法流程

基于IFS算法的经济负荷分配的流程如图1所示。

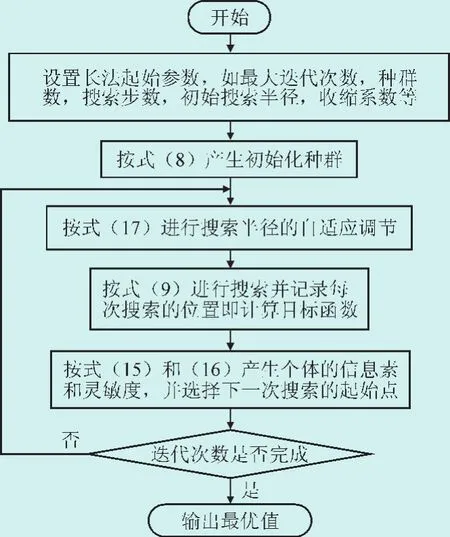
图1 基于IFS的经济负荷分配流程图

4 算例分析

本文以IEEE3机6母线标准测试系统为例进行计算分析，系统总负荷为500MW，发电机特性参数如表1所示。

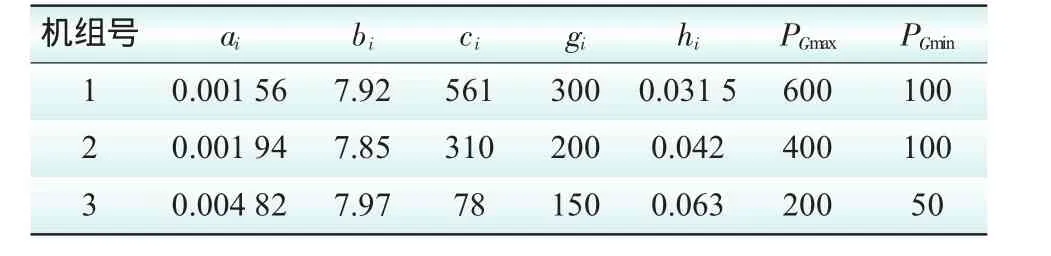
表1 IEEE 3机6母线机组参数

所用的B系数如下：

IFS算法参数设置如下：最大迭代次数Kmax=150；种群数N=30；搜索步数T=30；起始搜索半径Rij=1；搜索半径分界值R=0.01；收缩系数P1=0.98;P2=0.94。

为了便于与其他方案进行比较，本文目标函数分别考虑了以下3种情况：1）不考虑阀点效应，不考虑网损；2）考虑阀点效应，不考虑网损；3）考虑阀点效应，考虑网损。各种情况各自运行50次，GA、FS、IFS算法在寻优过程中最佳个体对应的发电成本进化曲线如图2所示，各种方案得到的最优解如表2～4所示。

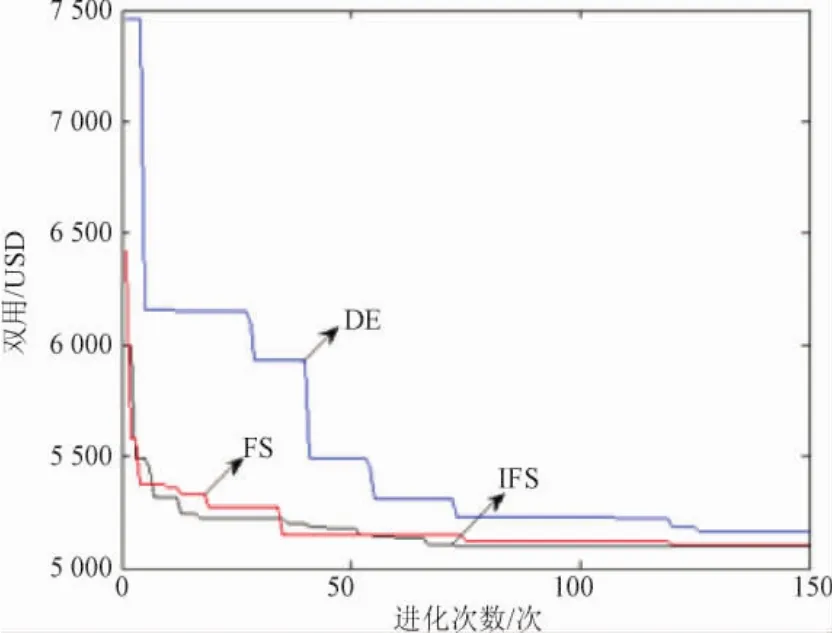
图2 情况2时几种算法的发电成本进化曲线

由图2可以看出，IFS算法收敛速度很快，大约70多代就搜索到最优解，明显优于GA算法，略优于FS算法，得到的最优解也较优。

由表2～4中可以看出：

1）对于情况1、2、3，经济负荷分配情况方案相差很大。因此在实际情况中建议应把阀点效应和网损都考虑进去才能得到正确结果。

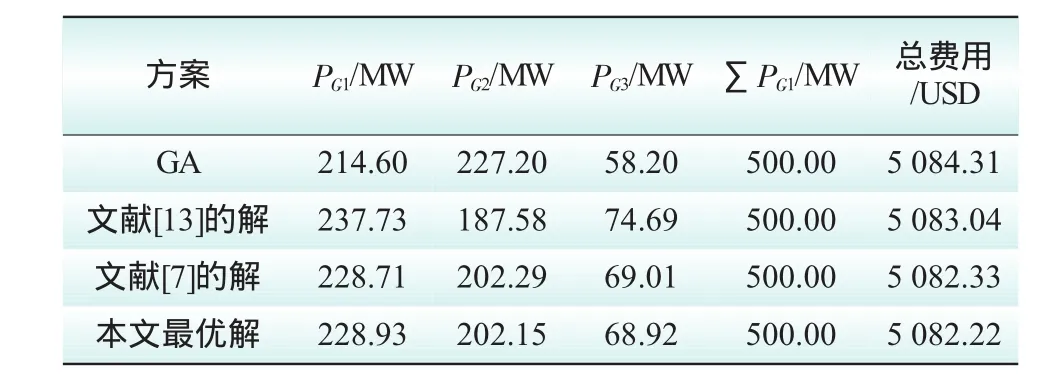
表2 情况1的结果

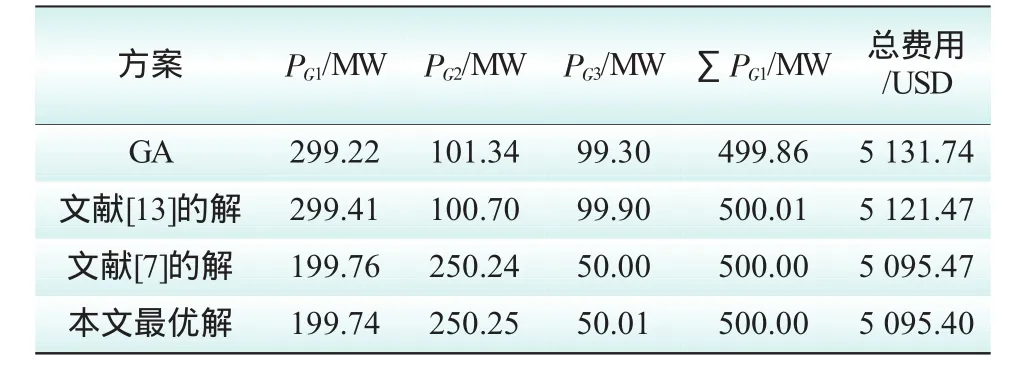
表3 情况2的结果

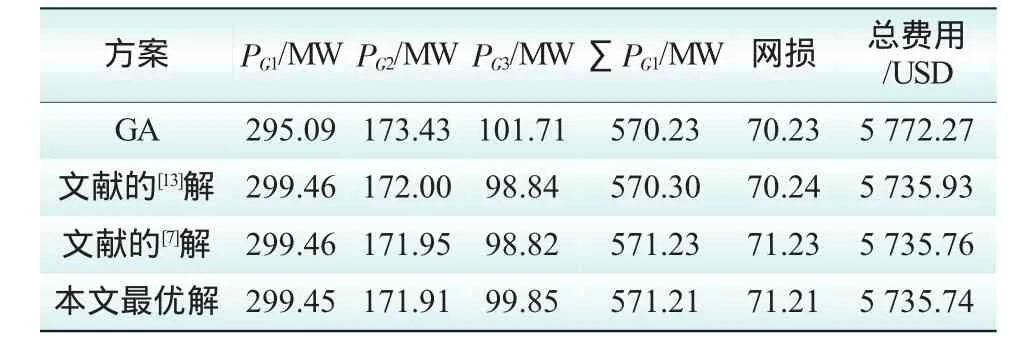
表4 情况3的结果

2）对于情况1、2、3，本文提出的改进自由搜索算出的总费用都明显优于遗传算法和文献[13]中的混沌优化方法，略优于文献[7]中的人工免疫混沌优化方法。因此可以得出IFS算法可以有效地解决电力系统经济负荷分配问题。

5 结语

自由搜索算法是一种新的集群智能算法，可以用于求解各种非凸、非线性优化问题。本文在标准FS基础上，修改了信息素和灵敏度产生方式，自适应调整了搜索半径，进一步提高了算法的寻优性能。在综合考虑网损和阀点效应等前提下，将IFS算法应用于电力系统经济负荷分配问题，通过经典算例证明了该算法的有效性和可行性。由于IFS是一种通用的优化算法，因此也可以用于求解电力系统其他优化类问题。

[1]侯云鹤，鲁丽娟，熊信艮，等.改进粒子群算法及其在电力系统经济负荷分配中的应用[J].中国电机工程学报，2004，24(7)：95-100.

[2]Farag A，Al-Baiyat S，Cheng T.Economic Load Dispatch Multi-objective Optimization Procedures Using Linear Programming Techniques[J].IEEE Trans.on Power Systems，1995，10(2)：731-738.

[3]吴磊，翟桥柱，管晓宏.发电经济调度可行解判据及其求解方法[J].电网技术，2004，28(1)：1-4.

[4]王剑奇，张伯明，赵子臣.动态比较法确定机组的最优组合[J].中国电机工程学报，1996，16(4)：254-256.

[5]David C，Gerald B.Genetic Algorithm Solution of Economic Dispatch with Valve Point Loading[J].IEEE Trans.on Power Systems，1993，8(3)：1325-1332.

[6]Lee Z.Particle Swarm Optimization to Solving the Dconomic Dispatch Considering the Generator Constraints[J].IEEE Trans.On Power Systems，2003，18(3)：1187-1195.

[7]蒙文川，邱家驹，卞晓猛.电力系统经济负荷分配的人工免疫混沌优化算法[J].电网技术，2006，30(23)：41-44.

[8]刘自发，张建华.一种求解电力经济负荷分配问题的改进微分进化算法[J].中国电机工程学报，2008，28(10)：100-105.

[9]Kalin Penev,Guy Littlefair.Free Search-a Comparative Analysis[J].Information Sciences,2005,172(1-2):173-193.

[10]周晖，李丹美，邵世煌，等.一种新的群集智能算法——自由搜索[J].东华大学学报：自然科学版，2007，33(5)：579-582.

[11]周晖，徐晨，邵世煌，等.自适应搜索优化算法[J].计算机科学，2008，35(10)：188-191.

[12]周晖，李丹美，邵世煌，等.一种新的群集智慧优化及其改进研究[J].系统工程与电子技术，2008，30(2):337-340.

[13]唐巍，李殿璞.电力系统经济负荷分配的混沌优化方法[J].中国电机工程学报，2000，20(10)：36-40.

Economic Dispatch of Power Systems Base On Based on Improved Free Search Algorithm

XIA Shu，ZHANG Jian-hua，QIU Wei，GE Xiao-lin
（School of Electric And Electronic Engineering，North China Electric Power University，Beijing 102206,China）

An improved free search ( IFS ) algorithm was presented based on the characteristic of nonconvex, nonlinear, multi- dimension for power systemeconomic load distribution. The searching efficiency and robustness are improved by adjusting the productionmethod ofpheromoneand sensibilityand usingthe plan of real- time controllingand searchingradius. The improved algorithm is used in computing of a typical example, and computed result is comparedwith that ofother optimization algorithm, it shows that IFS algorithmis effective in power systeme conomicloaddi stribution.

economic load distribution；free search；pheromone；sensibility;searching radius

针对电力系统经济负荷分配问题非凸、非线性、高维的特点，提出了一种改进自由搜索算法。通过调整个体信息素和灵敏度的产生方式，采用实时控制搜索半径的方案，进一步提高了此算法的寻优能力和鲁棒性。运用改进后的算法对一经典算例进行了求解，并将得到的结果与其他几种优化算法进行了比较，证明了该算法能有效地解决经济负荷分配问题。

经济负荷分配；自由搜索；信息素；灵敏度；搜索半径

1674-3814（2010）04-0037-04

TM744

A

2009-03-15

夏 澍（1987—），男，硕士研究究生，研究方向为电力系统规划。

（编辑 徐花荣）