弹性限位浮筏隔振系统的动力学建模与算法

温建明，冯 奇

（同济大学航空航天与力学学院，上海200092）

弹性限位浮筏隔振系统的动力学建模与算法

温建明，冯 奇

（同济大学航空航天与力学学院，上海200092）

文章从接触动力学的角度，建立多自由度多弹性限位浮筏隔振系统的动力学模型，采用人工神经网络算法用于判别限位器的接触状态。实例分析指出，神经网络算法接触判别的时间大大缩短，接触计算得以实现。得出了对工程有指导意义的结论：限位器单向约束时，筏体和设备的最大位移与限位器之间存在最优间隙。限位器双向约束时，筏体的最大位移与限位器之间存在最优间隙，而设备的最大位移随着限位器的间隙增大而增大。限位器间隙对系统的影响与限位器的约束状态有关。

浮筏；弹性限位；人工神经网络

1 引 言

含有限位器的浮筏隔振系统的抗冲击研究是一个涉及到非线性动力学，多自由度非线性系统建模、多刚体动力学、计算机仿真和优化等多种学科大分析计算问题。目前，国内外的研究比较集中在理论研究和试验研究相结合[1-2]。带限位器的浮筏系统在受到冲击作用时，限位器与设备之间的接触状态随着系统的振动会发生变化，这样就必须采用接触动力学模型描述，考虑撞击时间以及接触力。目前，对弹性限位器进行的非线性动力学研究主要都集中在单自由度系统[3-6]，对实际问题分析时主要借助于数值算法。Pfeiffer[7-8]建议采用拉格朗日乘子，将接触力预先乘入相应的雅可比矩阵，加在无接触的动力学方程上，并归之于LCP问题。Feng[9]提出了采用人工神经网络算法求解单边接触动力学问题，并通过索结构的计算得到了很好的验证。本文从接触动力学的角度，建立多自由度多弹性限位浮筏隔振系统的动力学模型，将人工神经网络算法用于判别限位器的接触状态。实例分析指出，神经网络算法接触判别的时间大大缩短，接触计算得以实现。同时研究了单向限位和双向限位两种限位状态下限位器间隙对浮筏系统受冲击情况下的影响。

2 弹性限位浮筏隔振系统的运动微分方程的建立

具有多个弹性限位器的浮筏隔振系统的简化模型如图1所示，浮筏隔振系统中的每个物体都看作具有六个自由度的刚体，隔振器简化为三向刚度的弹性元件，假设刚体转动时为小角度转动，取每个刚体的质心位移和卡尔丹角为广义坐标：

xi,yi,zi,αi,βi,γii=1,2,…

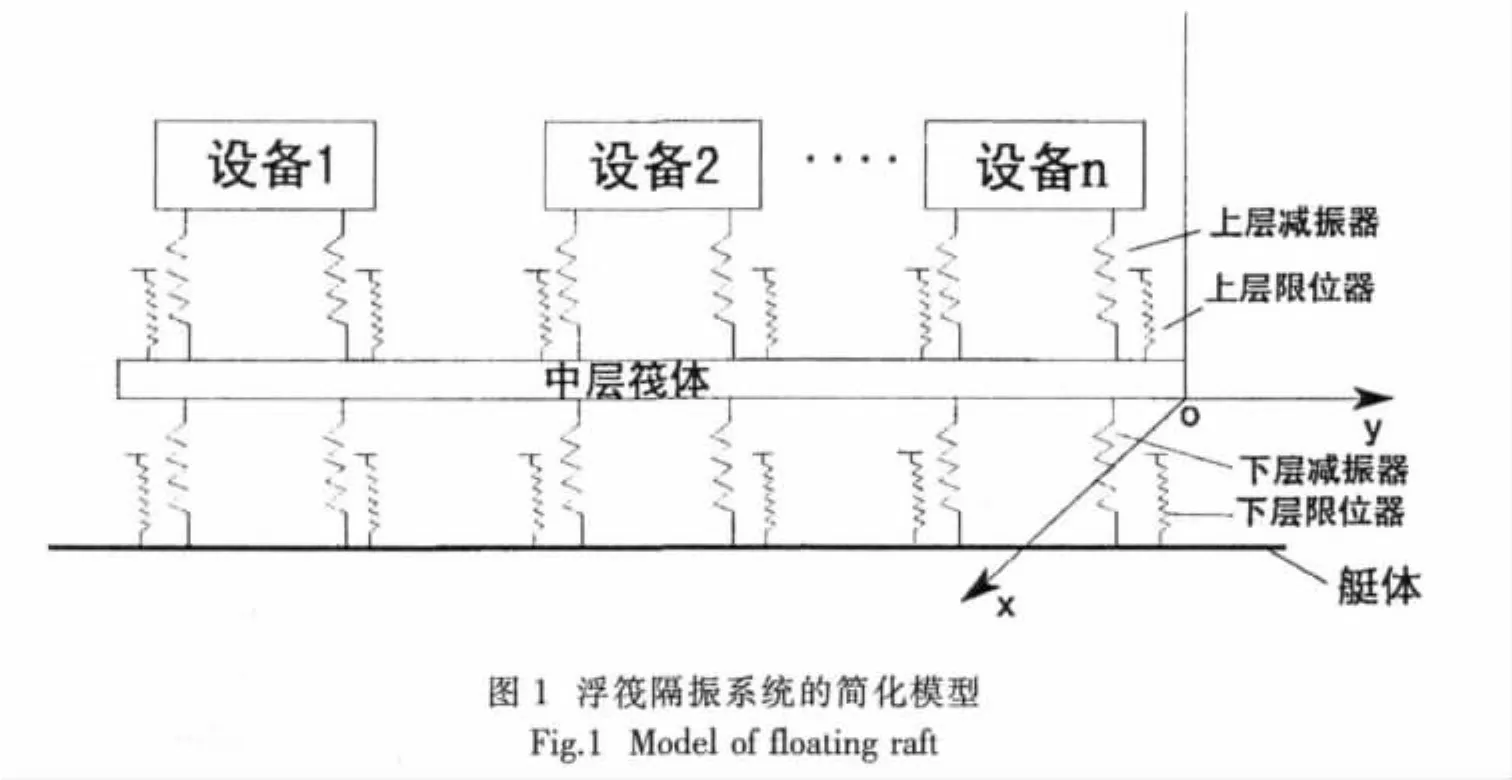
2.1 多刚体浮筏隔振系统的运动方程

对于隔振系统中的每一个物体，利用牛顿－欧拉方程，有如下形式[7]：

对于系统引入比例阻尼，产生系统的振动方程为：

2.2 弹性限位器的接触

如果gNi＞0，则物体n与限位器之间没有接触；如果gNi=0，则物体n与限位器之间接触；如果gNi＜0，则物体n与限位器之间接触并产生接触力。因此接触条件：

接触力对物体m质心的接触力矩：

接触力对物体n质心的接触力矩：

上式中，IBmA为物体m的连体基相对于惯性基的坐标转换阵，IBnA为物体n的连体基相对于惯性基的坐标转换阵。

一般地，如果有k个限位器，则每一个限位器最邻近点的距离都可以写成：

q为系统的广义坐标，由于wNi，i均为与时间无关的量，因此最邻近点的相对速度和相对加速度可写为：

用向量和矩阵的形式表示为：

2.3 含有接触力的浮筏隔振系统的运动微分方程

如果浮筏隔振系统在受到冲击作用，运动范围超出了其限位器的约束空间，此时弹性限位器与刚体发生接触，在隔振系统的运动方程中必须添加相应的接触力和接触力矩。设某时刻t，有nk个限位器发生接触，则添加接触力后的运动方程可写为：

另λNj=，表示接触力的大小，将上述方程进行整理，则运动微分方程可写为：

由于限位器只能承受压力，因此接触力向量λN中所有元素必须非负，即λN≥0。此外，接触点的相对加速度也必须非负，否则非穿透条件则不能满足。如果＜0，则意味着接触终止，其接触力相应地消失。如果=0，则物体仍旧保持着接触，接触力的大小λN≥0。因此对接触点存在着互补条件：

结合运动微分方程，系统可得到一个线性互补问题：

3 接触状态的决策

由于在浮筏隔振系统中存在的限位器比较多，当有多个可能的接触点存在时，接触的可能位形也有许多种可能。根据文献[7]可知，方程（17）的线性互补问题可以等价为优化问题，神经网络把优化问题中的目标函数约束条件与Hopfield的能量函数联系起来，那么电路达到的平衡点就是能量函数极小点，也是优化中满足约束条件下的目标函数的极小点。由于人工神经网络是并行计算，其计算时间不随维数的增加而发生指数性质的“爆炸”，因此用于判别限位器的接触状态很有效。

3.1 优化问题的目标函数

优化问题的关键是构造目标函数，在此利用高斯原理构造目标函数如下：

3.2 神经网络算法

根据要求的目标函数，设计Hopfield能量函数[10]E，令V=μ

Ri为电路中的电阻，令Ri=1，状态变量Z与输出变量V的关系为一硬函数：

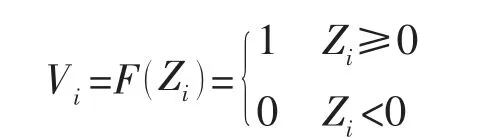
写成离散的反馈式网络为：

上述方程构成了神经网络的计算公式。网络参数W（t ），I（t）的具体表达式为：

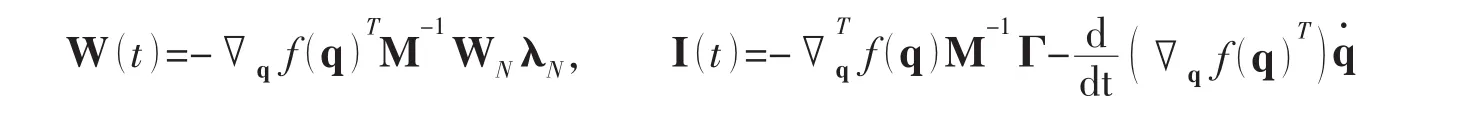
4 实例分析

浮筏隔振系统的筏体、设备的参数如表1。

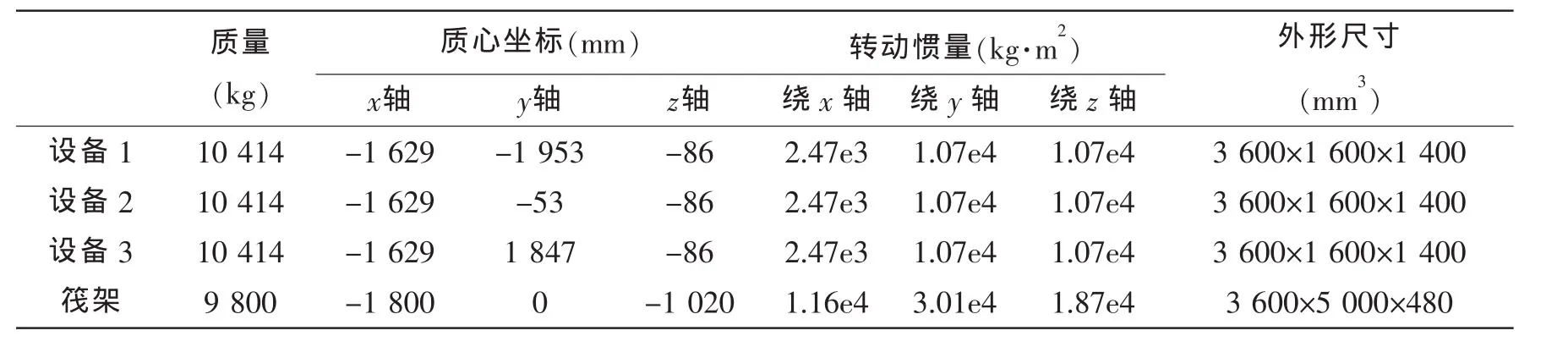
表1 浮筏基本参数Tab.1 Basic parameters of floating raft

上层组件共安装3×10只减振器和3×6只抗冲击限位器，减振器纵向刚度:1 715kN/m，横向刚度:1 715kN/m，垂向刚度:3 435kN/m。下层组件共安装3×12只减振器和3×6只抗冲击限位器，减振器纵向刚度:1 880kN/m，横向刚度:1 880kN/m，垂向刚度:3 760kN/m。下层限位器安装在基础上，上层限位器安装在筏体上，限位器的刚度取为隔振器的0.7倍，冲击作用的冲击加速度为50gsin 350（）τ，冲击时间为6ms。单向限位时限位器间隙为g0，双向限位时限位器间隙为±g0。g0≥（）0 。文中采用Matlab语言编制程序实现人工神经网络对限位器接触状态的决策[11]。

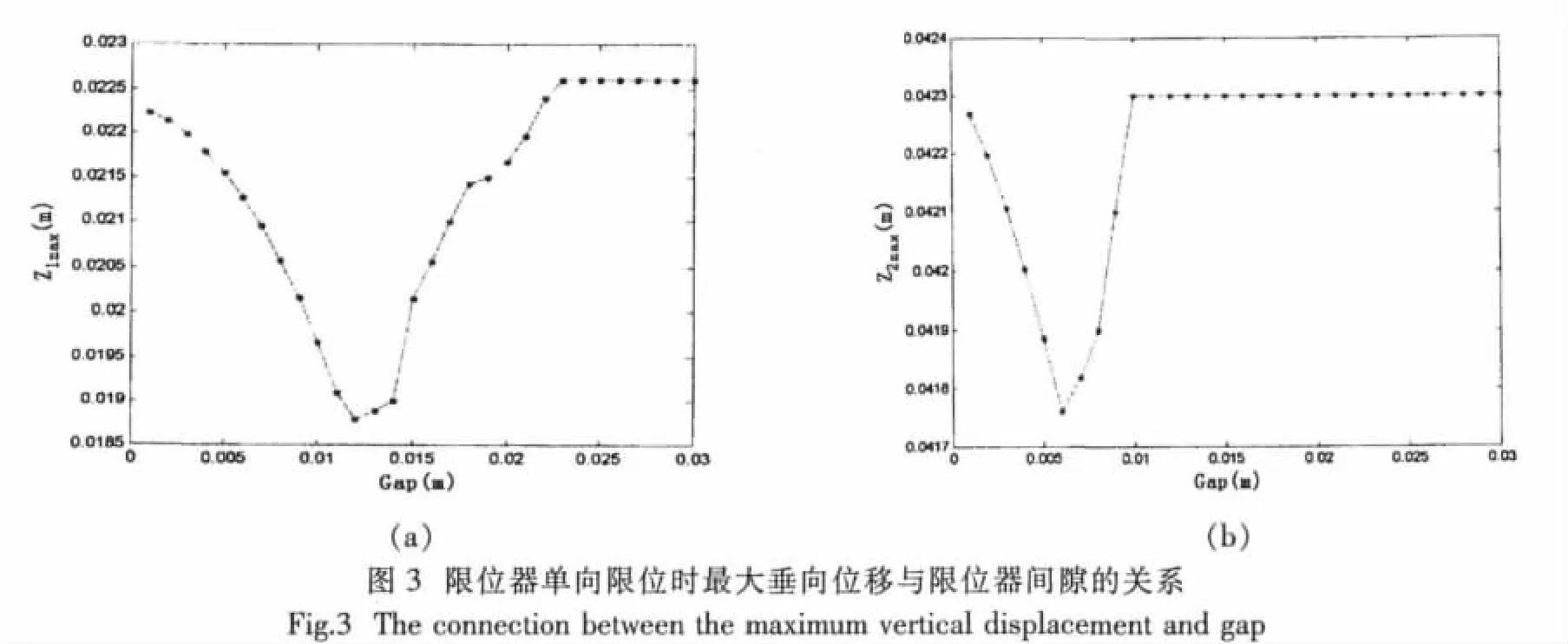
图3表示限位器单向限位时，浮筏隔振系统的冲击最大垂向位移与限位器间隙的关系，（a）为筏体的最大垂向位移与限位器间隙的关系，（b）为设备1的最大垂向位移与限位器间隙的关系，横坐标为限位器的间隙，纵坐标为最大垂向位移，z1max表示筏体的最大垂向位移，z2max设备1的最大垂向位移，可以看出，对筏体来说，冲击时最大垂向位移的最小值发生在限位器间隙为12mm的情况下，而当限位器间隙大于22mm时，限位器不起作用，为无限位器下的最大位移。而对于设备1来说，冲击最大垂向位移的最小值发生在限位器间隙为7mm，而当限位器间隙大于12mm时，限位器不起作用。因此，对于设计限位器间隙时，筏体的限位器间隙与设备的限位器间隙应分别设置，筏体的限位器间隙应大于设备的限位器间隙。这是由于筏体的限位器限制的是筏体的绝对位移，而设备的限位器限制的是设备与筏体的相对位移。

图4表示限位器双向限位时，浮筏隔振系统的冲击最大垂向位移与限位器间隙之间的关系图。图中横坐标为限位器的间隙，纵坐标为最大垂向位移，z1max表示筏体的最大垂向位移，z2max为设备1的最大垂向位移。可以看出，对于筏体来说，垂向最大位移在间隙为6mm的情况下达到了最小值。随着间隙的增大，垂向位移的最大值也在增大，当限位器间隙达到20mm时，限位器不再起作用。对于设备来说，随着限位器的间隙增大，垂向位移也增大。设备1当限位器间隙超过11mm时，限位器不起作用。双向限位器间隙对系统的影响与单向限位器间隙的影响是不同的。

5 结 论

本文建立了多自由度多弹性限位浮筏抗冲隔振系统的动力学运动微分方程，将人工神经网络算法用于判别限位器的接触状态。实例分析指出，神经网络算法的计算时间为直接搜索计算时间的1/1 000，接触判别的时间大大缩短。同时研究了单向限位和双向限位两种限位状态下限位器间隙对浮筏系统受冲击情况下的影响，指出了限位器单向约束时，筏体和设备的最大位移与限位器之间存在最优间隙，筏体的最优间隙与设备的最优间隙是不同的，应分别设置。限位器双向约束时，筏体的最大位移与限位器之间存在最优间隙，而设备的最大位移随着限位器的间隙增大而增大。限位器间隙对系统的影响与限位器的约束状态有关。

[1]William T F.UNDEX testing:When,why&how it began[C]//Proceedings of the 70th Shock and Vibration Symposium,Albuquerque,New Mexico,USA,1999:15-19.

[2]Van Ananhold J E,Meijer G J,Lemmen P P M.Under shock response analysis of a floationg vessel[J].Shock and Vibration,1998,5:53-59.

[3]胡海岩.隔振系统限位器的非线性动力学设计[J].航空学报,1996,17(5):529-533.

[4]Narayanan S,Sekar P.Periodic and chaotic responses of an SDF system with piecewise linear stiffness subjected to combined harmonic and flow induced excitations[J].Journal of Sound and Vibration,1995,184(2):281-298.

[5]Chicurel-Uziel E.Exact,single equation,closed-form solution of vibrating systems with piecewise linear springs[J].Journal of Sound and Vibration,2001,245(2):285-301.

[6]Chatterjee S,Malik A K,Ghosh A.Periodic response of piecewise non-linear oscillators under harmonic excitation[J].Journal of Sound and Vibration,1996,191(1):129-144.

[7]Pfeiffer F,Glocker C.Multibody dynamics with unilateral contacts[M].Cambridge,UK:Wiley,1996.

[8]Pfeiffer F.Mechanical system dynamics[M].New York:Springer,2008.

[9]Feng Q,Tu J.Modeling and algorithm on a class of mechanical systems with unilateral constraints[J].Archive of Applied Mechanics,2006,76(1-2):103-116.

[10]张立明.人工神经网络的模型及其应用[M].上海:复旦大学出版社,1993.

[11]葛哲学,孙志强.神经网络理论与MATLAB R2007实现[M].北京:电子工业出版社,2007.

Model and algorithm for floating raft with elastic limiters

WEN Jian-ming,FEN Qi

(School of Aerospace Engineering and Applied Mechanics,Tongji University,Shanghai 200092,China)

Based on contact dynamics,the multi-degree-freedom dynamic model of floating raft isolation system with elastic limiters was established.The artificial neural network was used to dingtinguish the contact state of elastic limiters.The example analysis showed that the algorithm of artificial neural network for contact shortened the time of caclaution.The contact calculation could be realized.Some interesting results may be useful to the actual engineerings:for setting an unilateral limiter to the system,there is a best gap corresponding to the displacement of the raft and equipments.Setting the bilateral limiter to the system,there is a best gap corresponding to the raft.On the other hand,the maximum displacement of the equipment is increased with the limiter’s gap.The influence of gap for floating raft is concern of the constraints’status.

floating raft;elastic limiter;artificial neural network

032

A

1007-7294（2010）05-0549-07

2009-05-23

国家自然科学基金（10702051）：随机非光滑系统中的摩擦和接触研究（Friction and contact in stochastic nonsmooth system）；上海市重点学科建设项目资助（B302）

温建明（1972-），女，同济大学航空航天与力学学院副教授，wenjianming@tongji.edu.cn。