2种纤维弹塑性梁单元特性

聂利英,郭青伟,李硕娇

(河海大学土木与交通学院,江苏南京 210098)

钢筋混凝土是由2种不同的材料——混凝土和钢筋组合而成的,其性能与这2种材料的性能密切相关,特别是在非线性阶段,混凝土和钢筋本身的各种非线性特征,在这种组合材料中会有一定程度的反映.

对于压弯构件,一般在截面层次建立恢复力模型.常用的一般空间受力杆件恢复力模型有3种:屈服面模型[1]、多弹簧模型[2-3]和纤维模型[4-5].纤维模型将梁柱截面沿2个主轴方向划分成网格(纤维),每一根纤维可以表示混凝土,也可以表示钢筋.分析时,基于平截面假定和钢筋、混凝土纤维各自的应力 应变关系,考虑2个方向弯矩平衡条件和轴力平衡条件,可获得复杂的截面双向滞回曲线.

目前基于纤维模型的钢筋混凝土弹塑性梁柱单元有2种:一种是沿单元长度积分的纤维弹塑性梁单元,根据单元长度方向的内力分布,可以求得各截面的弯曲刚度,沿单元长度积分可以得到单元刚度,这种单元可以模拟受力过程单元长度方向截面刚度的连续变化;另一种是可以直接应用塑性铰长度经验公式的单元——带长度的纤维塑性铰弹塑性梁单元,其塑性变形集中在一定长度范围的塑性铰上,这种单元只在塑性铰范围内采用.本文首先对这2种单元模型及其本构特征进行分析,然后应用这2种单元对一桥梁工程进行地震反应分析,从静力和动力2个方面对比了这2种单元的主要非线性特性.

1 2种弹塑性梁单元的对比

1.1 基本假定

2种单元的基本假定有相同之处,也有不同之处.相同之处是,2种单元均基于以下假定:(a)小变形假定;(b)平截面假定;(c)忽略黏结滑移和剪切滑移影响;(d)扭转为弹性且不与弯矩、轴力耦合.不同之处是:沿单元长度积分的纤维弹塑性梁单元将一个梁单元划分为若干积分段,假定每段内,截面形式和截面上各个纤维的本构关系保持一致;带长度的纤维塑性铰弹塑性梁单元假定在塑性铰长度范围内,刚度性质保持一致.

1.2 本构模型

1.2.1 沿单元长度积分的纤维弹塑性梁单元

由图1可知,沿单元长度积分的纤维弹塑性梁单元的本构模型比较简单.这种单元的特点是沿单元轴向离散成许多段,每一段的特性由中间横截面(或切片)的特性来代表,而该横截面又被离散成许多纤维(如用矩形网格划分),每一根纤维都可直接定义混凝土或钢筋的应力-应变关系,并且由截面上的力和变形关系可以得到截面上的刚度矩阵

其中

式中E(x,y,z)为轴向坐标为x,截面坐标为y,z的钢筋或混凝土纤维的弹性模量,其大小与纤维受力过程中的应力状态有关,可直接通过钢筋或混凝土的应力 应变关系曲线获得.已知梁单元每一个积分段截面的刚度矩阵,即截面绕y,z轴的曲率、轴向应变与截面绕y,z轴的弯矩、轴向力之间的关系,沿单元轴线积分,则可得到单元杆端的力与位移关系,即单元刚度矩阵.由此可见,此模型可以描述单元内部每一个积分段代表截面的曲率变化.

图1 2种纤维弹塑性梁单元Fig.1 Two fiber elastop lastic beam-column elements

1.2.2 带长度的纤维塑性铰弹塑性梁单元

这种单元实际上是一种分布塑性铰模型,可通过子单元法来建立,如图1(b)所示.子单元法是建立钢筋混凝土弹塑性梁单元的常用方法,最早由Giberson[6]提出,后来被广泛应用.Imbsen等[7]于1986年利用子单元法建立了屈服面集中塑性铰弹塑性梁单元模型,Filippou等[8]于1988年利用子单元法建立了集中塑性铰模型,后来又建立了分布塑性铰模型.

子单元法[8-9]认为:压弯构件弹塑性变形可以分为弹性变形和塑性变形2个部分,这2种变形可分别用弹性子单元和刚塑性子单元来模拟,单元的柔度为各个子单元柔度的和,如图1(c)所示.弹性子单元为一般的空间弹性梁单元,仅发生弹性变形;刚塑性子单元的塑性变形集中在塑性铰区,塑性铰之间由刚性杆连接,塑性铰长度范围内刚度性质保持一致.

当采用子单元法建立单元模型时,以双折线本构模型为本构关系的子单元分解相对容易实现.双折线本构模型考虑了强化阶段的弯矩(M)曲率(φf)关系,可以近似表达截面的刚度变化规律,其恢复力关系曲线如图2所示.图2中:dφf为曲率增量;(dφf)e为弹性曲率增量;(dφf)p为塑性曲率增量;EI为截面弹性弯曲刚度,EI=,I为截面惯性矩;(EI)T为截面进入塑性强化阶段的弯曲刚度,(EI)T=.图 2 中的截面M-φf关系可以分解为弹性和刚塑性2个部分,如图3所示.

H′对应刚塑性模型强化阶段,因此有

由式(2)和图3可知,2个部分的弯矩 曲率关系构成串联模型,如图4所示.由此子单元法的建模过程可知,弹塑性梁单元由弹性子单元与刚塑性子单元串联而成,其中EI对应弹性子单元本构特征,H′对应刚塑性子单元本构特征,My即为屈服弯矩,用来判断结构是否进入塑性阶段.

图2 梁单元截面的双折线强化恢复力关系Fig.2 Bilinear hysteresis curve of beam section

图3 梁截面M-φ关系分解结果Fig.3 Decomposition of moment-curvature relation of beam section

图4 串联模型Fig.4 Series model

带长度的纤维塑性铰弹塑性梁单元的刚塑性子单元的刚塑性采用纤维模型来描述,与前述分解双线性截面弯矩 曲率关系的思路相对应,将钢筋和混凝土的应力(σ)-应变(ε)关系理想化为双线性的强化模型,如图5(a)所示.由于刚塑性杆子单元中没有弹性变形,因此其截面上的钢筋、混凝土纤维的应力 应变关系为刚塑性模型,如图5(b)所示.类似于式(2)的曲率刚塑性强化参数H′,图5(b)中h′s为刚塑性应变强化参数,由式(3)求得.

式中E′为塑性段的斜率.虽然此单元的塑性特征最终是通过钢筋和混凝土的刚塑性应力和应变来反映的,但是从子单元法分解本构模型的总体思路可以看出,此单元的塑性铰区域总体上应该能够体现双折线强化模型的特点.

图5 纤维 σ-ε关系Fig.5 Relationship between stress and strain of fiber

1.3 适用性

a.2种单元均将梁柱截面沿2个主轴方向划分成网格(纤维),每一根纤维都可直接定义混凝土或钢筋的应力 应变关系,根据截面上2个方向的弯矩平衡条件和轴力平衡条件,求得截面的双向滞回曲线,因此,这2种单元对于复杂截面均具有很好的适用性.

b.沿单元长度积分的纤维弹塑性梁单元在计算分析钢筋、混凝土的应力 应变关系时可方便地采用多折线模型,且沿着单元长度积分可以得到总体单元刚度矩阵.因此,纤维弹塑性梁单元可模拟梁柱受力过程中沿单元长度方向截面刚度的连续变化过程,精细地反映梁柱开裂、屈服等非线性性能.

c.带长度的纤维塑性铰弹塑性梁单元,其塑性铰特征总体上能体现双折线强化模型的特点,且塑性铰长度为单元模型参数.因此,可以利用塑性铰长度的经验公式,将此单元与实践经验相结合.

2 实 例

为了比较这2种弹塑性梁单元的应用特性,本文通过一联连续梁桥的地震反应分析比较其动力响应,并在单墩模型的能力分析中比较二者的力 位移关系曲线.

图6 7跨连续桥计算模型Fig.6 Analytic model of continuous bridge with 7 spans

2.1 连续梁模型

计算模型如图6所示.其中:2个边墩墩顶为滑板支座,其余墩顶支座为橡胶支座且设有限位器;所有墩截面的长×宽均为200 cm×90cm,混凝土等级C30,纵筋配筋为54∅22,且纵筋沿四周均匀布置.由于桥梁震害主要集中在下部墩体,分别用2种弹塑性梁单元模拟墩柱,进行静力推倒分析和动力时程分析.建模要点如下:(a)基底固接.(b)桥墩分别用纤维弹塑性梁单元和纤维塑性铰弹塑性梁单元模拟.分析中纤维截面划分为3种类型,即保护层混凝土、核心混凝土和钢筋.混凝土中箍筋的作用通过约束混凝土的本构关系来考虑[10-11].(c)2个边墩墩顶滑板支座用2个水平小刚度弹簧和1个竖向大刚度弹簧来模拟,其他墩顶与梁体连接用3个平动大刚度弹簧来模拟.(d)上部结构取为弹性梁单元,且为单梁模型.(e)采用集中质量模型.

分析过程中,地震波的输入方向分为纵、横向,纵向为计算模型第1个和最后1个墩的连线方向,横向为与纵向垂直的方向.本文采用罕遇水准地震波,对这一联连续梁进行分析.

2.2 桥墩能力分析

首先对各个桥墩进行单墩静力推倒分析.图7为7号墩用2种单元模拟时静力推倒力 位移关系分析结果.

图7 7号墩静力推倒力 位移关系分析结果Fig.7 Analytic results of static push-over force-disp lacement relation of pier No.7

由图7可见,沿单元长度积分的纤维弹塑性梁单元可以精细地模拟受力过程中沿杆长方向截面刚度的连续变化过程,带长度的纤维塑性铰弹塑性梁单元则反映出明显的双线性特征,且2种弹塑性梁单元的计算结果相近.由此可见,带长度的纤维塑性铰弹塑性梁单元是对沿单元长度积分的纤维弹塑性梁单元的一种近似.

通过对2号～7号墩的静力推倒分析,得到不同墩高下的屈服位移(以纤维塑性铰弹塑性梁单元模拟桥墩的模型为准),见表1.

2.3 动力时程分析

表2和表3为连续梁动力计算结果.由表2和表3可知:在罕遇地震下,地震波横向输入时,6号墩接近屈服状态,其他墩均发生屈服;墩顶位移和墩底内力,除6号墩略有差异外,2种弹塑性梁单元模型计算结果吻合较好.地震波纵向输入时,2号～4号墩发生屈服,5号～7号墩未屈服;2种弹塑性梁单元模型计算情况下,墩顶位移和墩底内力结果差异略大.

表1 连续梁各墩墩顶屈服位移Table 1 Yield displacements of continuous bridge at pier tops

表2 地震波横向输入连续梁动力计算结果Table 2 Dynam ic results of continuous bridge under transverse seism ic waves

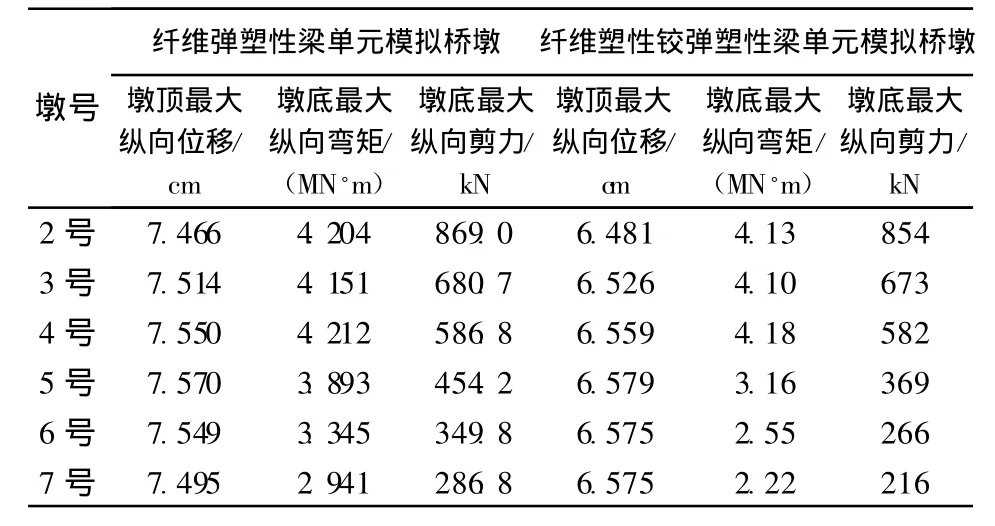
表3 地震波纵向输入连续梁动力计算结果Table 3 Dynam ic results of continuous bridge under longitudinal seism ic waves

3 结 论

a.沿单元长度积分的纤维弹塑性梁单元可以模拟受力过程中沿杆长方向截面刚度的连续变化过程,带长度的纤维塑性铰弹塑性梁单元则可以反映双线性特征.从静力推倒分析得到的力 位移关系曲线可以可明显地看出此双线性特征.

b.带长度的纤维塑性铰弹塑性梁单元是对纤维弹塑性梁单元的一种近似.2种弹塑性梁单元在构件是否屈服的判断上结果完全相同,而且当构件全部或几乎全部屈服时,其动力响应吻合很好;但是当有显著的未屈服构件影响时,分析结果差异相对略大.这表明,当结构在动力作用下发生强烈的塑性响应时,2种弹塑性梁单元均可恰当地描述结构的塑性特征,否则会有较大差异.这主要是由于未屈服前,沿单元长度积分的纤维弹塑性梁单元,其各积分段的刚度连续变化,可以有效反映开裂等刚度退化现象,而带长度的纤维塑性铰弹塑性梁单元此时刚塑性子单元不参与工作,单元刚度为弹性子单元刚度.

[1]TAKIZAWA H,AOYAMA H.Biaxial effects inmodeling earthquake response of R/C structures[J].Earthquake Engineering&Structural Dynamics,1976,4(6):523-552.

[2]LAI S S,WILL G T.R/C space frames with column axial force and biaxial bending moment interactions[J].J Struc Eng,1986,112(7):1553-1572.

[3]LI K N.Nonlinear earthquake response of reinforced space frames[D].Tokyo:University of Tokyo,1993.

[4]SPACONE E,FILIPPOU F C,TAUCER F F.Fiber beam-column model for nonlinear analysis of R/C frames:part I formulation[J].Earthquake Engineering&Structural Dynamics,1996,25(7):711-725.

[5]SPACONE E,FILIPPOU F C,TAUCER F F.Fiber beam-column model for nonlinear analysis of R/C frames:part II application[J].Earthquake Engineering&Structural Dynamics,1996,25(7):727-742.

[6]GIBERSON M F.Two nonlinear beams with definition of ductility[J].Journal of the Structural Division,1969,95:137-157.

[7]IMBSEN R A,PENZIEN J.Evaluation of energy absorption characteristics of highway bridges under seismic conditions:report of EERC[R].Berkeley:University of California Berkeley,1984.

[8]FILIPPOU F C,ANGELO A D,ISSA A.Nonlinear static and dynamic analysis of reinforced concrete sub assemblages:report of EERC[R].Berkeley:University of California Berkeley,1992.

[9]欧文 D J R,辛顿E.塑性力学有限元[M].曾国平,译.北京:兵器工业出版社,1989.

[10]MANDER J B,PRIESTLEY M J N,PARK R.Theoretical stress-strain model for confined concrete[J].Journal of Structural Enginnering,1988,114(8):1804-1826.

[11]MANDER J B,PRIESTLEY M J N,PARK R.Observed stress-strain behavior of confined concrete[J].Journal of Structural Enginnering,1988,114(8):1827-1849.