建筑物的定位放样方法及其误差分析

朱 勇 邹宗良

建筑物的定位放样工作,就是要将建筑物的平面位置在实地上标定出来,其实质是将建筑物的一些轴线交叉点、拐角点测设在地面上,它是建筑工程测量的主要任务之一。在施工现场,由于干扰因素很多,测设方法和计算方法力求简捷,放样精度应根据建筑工程的性质和设计的要求来确定,不需片面追求高精度,导致人力、物力及时间的浪费;但也不应过低而影响施工质量,甚至造成工程事故。本文将首先分析建筑物定位放样的精度要求,然后讨论极坐标法和角度交会法放样的误差问题,从而为建筑工程进行定位放样时合理的选择放样方案提供参考。

1 建筑物定位的点位放样精度要求

建筑物定位的点位测量中误差 m测受施工控制点的起算误差m控和放样误差m放的共同影响,即:

由文献[1]可知:点位测量中误差和建筑限差之间的关系为m测=±N◦Δ,N=1/3～1/2;当 N=0.4时,m控=±0.082Δ,m放=±0.182Δ;当 N=0.5时,m控=±0.102Δ,m放=±0.228Δ。

其中,Δ为建筑限差。

建筑限差是施工点位相对纵横轴线偏离值的限值,在现行的国家标准GB 50300建筑工程施工质量验收统一标准及GB 50202～GB 50209各专业工程施工质量验收规范等规范中,均作了明确规定。建筑限差的大小,是根据工程建筑物的规模和性质来决定的。若取建筑限差分别为10mm,20mm,50mm,则我们可得建筑物定位的点位测量中误差如表1所示。

表1 建筑物定位的点位测量中误差 mm

2 点位放样方法及其误差分析

2.1 施工控制网的放样误差分析

施工测量贯穿于整个施工过程中,其首要任务就是建立施工测量控制网。施工控制网通常分为场区控制网和建筑物施工控制网,对于规模较小的单体项目或当项目间无刚性连接时,可根据实际情况,减少施工控制网的布网层次,直接布设建筑物施工控制网。控制点的点位精度可以用下式计算:

其中,mij为相邻点的点位中误差为边长相对中误差;mβ为测角中误差;Sij为相邻点间边长。

当采用全站仪布设施工控制网时,根据全站仪的不同标称精度和不同的放样距离,按式(2)可得控制点的放样误差如表2所示。

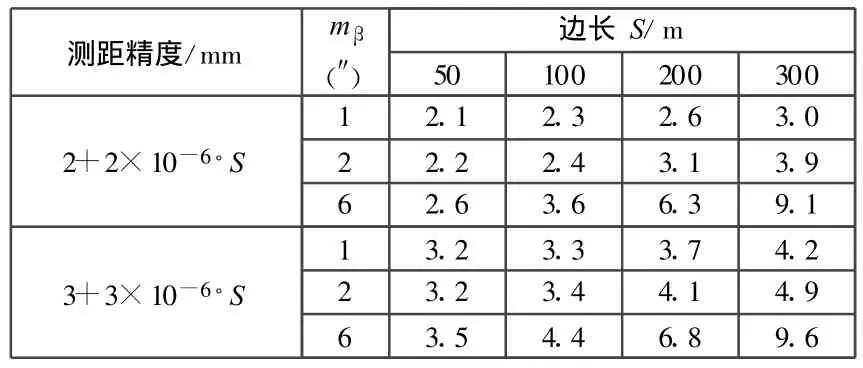
表2 控制点点位放样误差

比较表1和表2中的数据,结果表明,若建筑限差 Δ≥20mm时,测距精度为2+2×10-6◦S,测角精度为1″和2″的全站仪基本能满足放样精度要求。

2.2 建筑物定位的点位放样方法及其误差分析

建筑物的定位是根据已布设好的控制点与放样点间的角度(方向)、距离或相应的坐标关系而定出点的位置。常见的放样方法有直角坐标法、极坐标法、角度交会法、距离交会法和全站仪坐标放样法等。工程中可根据所用的仪器设备、控制点的分布情况、放样场地地形条件及放样点精度要求等从中选择使用。现分析用极坐标法和角度交会法放样点位的精度。

1)极坐标法。采用极坐标法放样点位时,点位放样误差可用下式计算:

其中,mP为放样点点位中误差;ms为边长中误差;mβ为角度中误差;S为测站点至放样点的距离。

若不考虑标定误差,用不同的测距误差、测角误差和边长代入式(3),可得极坐标放样法的点位误差,见表3。

表3 极坐标放样法的点位误差

比较表1和表3中的数据,测距精度越高,放样误差则越小;而测角精度的高低,对放样误差的影响很微小。当测距中误差大于1/5000时,点位放样误差远超过了误差要求;当测距中误差小于1/5000时,放样边长越大,点位误差也越大,两者成正比的关系,但只要选择合适的边长,点位放样误差能满足要求。

2)角度交会法。角度交会法,适用于不便量距或测设点远离控制点的地方,见图1。对于一般小型建筑物或管线的定位,亦可采用此法。测设点P的精度可按下式计算:

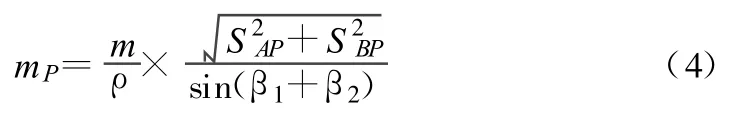
其中,mP为放样点点位中误差;β1,β2均为交会角;m为测设β1,β2的测角中误差;SAP,SBP均为交会边的长度。

若不考虑标定误差,选择不同的交会角和交会边长度代入式(4),可得角度交会法的点位放样误差,见表4。

从表4的计算结果可以看出,若不考虑点位标定误差,角度交会法的放样误差小于极坐标法放样误差;当交会边长度小于200m时,只要两交会角之和的正弦值不太小,点位放样误差能满足要求。

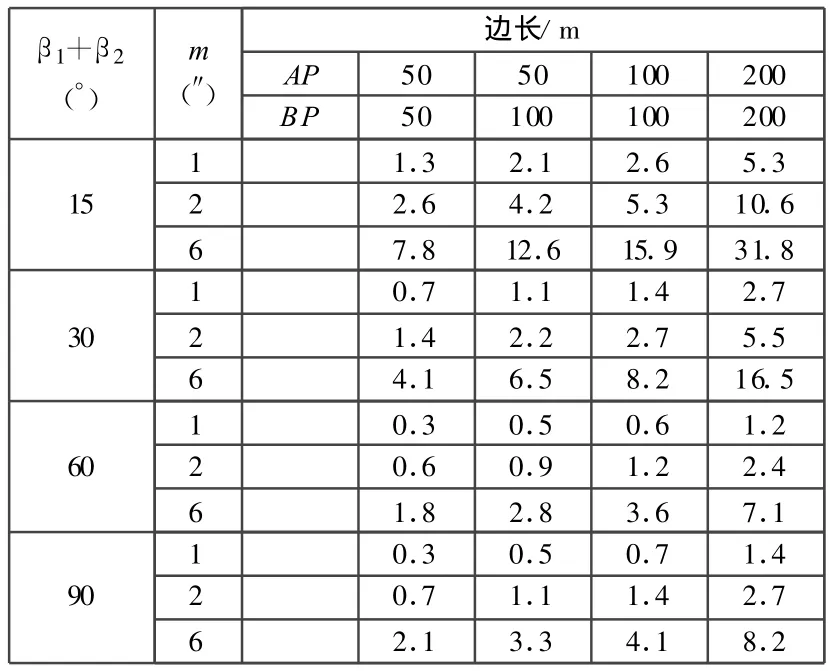
表4 角度交会放样法的点位误差

3 结语

1)施工测量贯穿于整个建筑施工的全过程,放样精度对建筑工程质量和施工进度都起着十分重要的作用,应合理确定测量误差与施工误差的关系,控制点误差与放样误差的关系。2)用极坐标法进行点位放样时,要合理确定放样方案,选择合适的测边精度与测角精度,以减少点位放样误差。3)用角度交会法进行点位放样时,要合理确定交会角度和距离,同时尽量减少点位标定误差,以提高点位放样精度。

[1]王黎黎,杨志藻.建筑施工测量必要精度的探讨[J].工程勘察,2000(2):59-61.

[2]DB 50026-2007,工程测量规范[S].

[3]陈丽华.测量学[M].杭州:浙江大学出版社,2009.