具有中介状态结构地震易损性分析

李 明 鲍雷华 陈红敏

地震易损性分析就是估计建筑结构在某强度地震作用下,发生给定破坏等级的概率。根据我国三级抗震设防原则“小震不坏、中震可修、大震不倒”,将结构的破坏等级分为安全、中介、失效三级。其中安全状态对应结构完好和轻微破坏,中介状态对应结构的中等破坏,失效状态对应结构严重破坏和倒塌。这里的易损性分析就是计算不同烈度地震作用下,结构处于安全、中介、失效的概率,通过计算不同烈度下结构的可靠性向量,得到可靠性矩阵,即为单体结构易损性矩阵。在单体结构易损性矩阵基础之上,通过概率方法,计算得到群体建筑易损性矩阵,矩阵中的数据表示某强度地震作用下,发生给定破坏等级建筑所占抽样建筑的比例。

1 单体建筑易损性分析

根据震害的严重程度,将结构在地震作用下可能发生的破坏等级划分为三级,每级破坏分别对应结构的安全状态、中介状态和失效状态。文献[1]将建筑的破坏程度划分为五级,基本完好(B1)、轻微破坏(B2)、中等破坏(B3)、严重破坏(B4)、倒塌(B5)。用Dj表示第j级破坏等级,则:

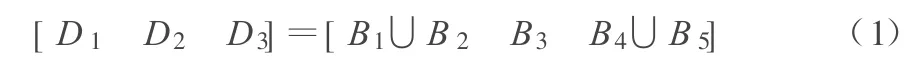
三级破坏等级D1,D2和D3分别对应安全、中介、失效三级工作状态,这样地震易损性分析就是计算结构在某强度地震作用(烈度 i)下,处于安全、中介和失效状态的概率:

其中,Pij为强度为I的地震作用下,设防烈度为Id结构发生第j级破坏的条件概率。

通过式(2),可以计算某一烈度作用下,结构处于安全、中介和失效的概率PR,PM,PF得到结构的可靠性向量[PR,PM,PF]。不同地震烈度可以计算得到不同的可靠性向量,以可靠性向量为行,可以得到可靠性矩阵 Pi×j:

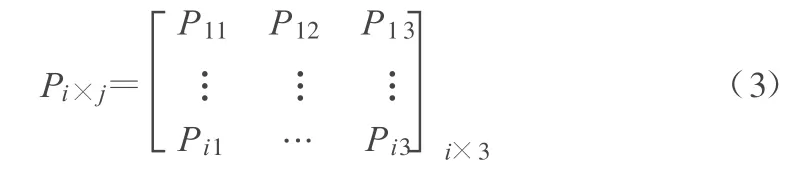
矩阵Pi×j中的各元素表示在某烈度i地震作用下,结构发生第j级破坏的概率,即此矩阵就是三级破坏等级对应的易损性矩阵。矩阵的行代表某烈度i地震作用下结构的可靠性向量,显然Pi1+Pi2+Pi3=1。

2 建筑群体易损性分析

建筑结构群体易损性分析就是确定一个城镇、地区或者企业范围内,按照某种分类标准的同类建筑在某强度地震作用下发生某种破坏程度的概率。通过群体易损性分析可以反映不同城镇、地区建筑物的抗震性能和不同种类建筑的抗震性能。文献[2]提出了一种根据计算平均震害指数来快速评估城镇地区群体震害方法;高小旺等分别对城市和企业,以及内框架和底框建筑进行震害预测研究,并提出了基于概率的预测方法[3-5]。尹之潜以概率理论为基础,提出了地震灾害预测的动态分析模型,得到了计算动态震害矩阵和动态损失矩阵的方法,为震害的动态分析打下了理论基础[6,7]。陈健云等将模糊数学中的熵权法和相似理论引入到建筑群体易损性评估中,提出了一种适用于震后快速评估的分析方法,并用于分析砌体结构[8]。

通过分析预测单元中抽样得到的单体结构,我们可以得到各个单体结构的可靠性向量。在计算群体易损性矩阵的时候,把每栋建筑的破坏看成是一个随机过程Ai,在某地震烈度作用下,建筑破坏这个随机过程具有三个基本事件Ai1,Ai2,Ai3,其中Ai1发生的概率为结构处于安全的概率、Ai2发生的概率为中介概率、Ai3发生的概率为失效概率。对于抽样得到的N栋建筑在地震作用下的破坏,就相当于进行N次独立试验,每次试验的基本事件为Ai1,Ai2,Ai3,根据各个事件发生的概率,就可以求得 N次事件中发生n次Ai1(或者 Ai2,Ai3)事件的概率,即得到 N栋建筑中有n个建筑处于安全(或中介、失效)的概率 PR(n/N)(或PM(n/N),PF(n/N)),即为有 n栋建筑发生D1(D2和D3)级破坏的概率,这样我们就可以得到 N栋建筑中发生D1(D2和D3)级破坏的概率期望ER(n/N),EM(n/N)和EF(n/N)。根据离散分布函数期望的定义:

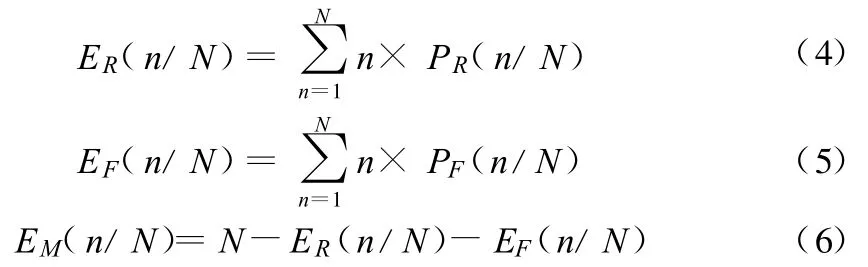
为了简化计算,将可靠性向量蜕化为二维模型[安全,非安全]和[非失效,失效],然后计算得到 PR(n/N)和 PF(n/N),进而根据式(4),式(5)算出对应 D1,D3级破坏建筑数的期望,然后通过式(6)得到 EM(n/N)。然后根据式(7)计算 i级地震烈度下,发生第 j级破坏的概率。

其中,Rij为所有抽样建筑在发生i级地震烈度作用时,发生j级破坏建筑占抽样建筑总数的百分比;Eij(n/N)为某烈度 i地震作用下,发生 j级破坏建筑数的期望值,按式(4),式(5)和式(6)计算。根据式(7),可以得到群体建筑的易损性矩阵:

矩阵中的每个元素为在某烈度地震作用下,发生某级破坏建筑的数量与抽样建筑总数的比值。

3 计算实例

考虑地震烈度为7度,抽样建筑数量为5栋,其中每栋建筑在烈度7度条件下的可靠性向量分别为[0.85,0.11,0.04],[0.63,0.29,0.08],[0.83,0.10,0.07],[0.79,0.15,0.06],[0.75,0.20,0.05]。将可靠性向量蜕化为二维模型[安全,非安全],相应的概率为[0.85,0.15],[0.63,0.37],[0.83,0.17],[0.79,0.21],[0.75,0.25];[非失效,失效]相应的概率为[0.96,0.04],[0.92,0.08],[0.93,0.07],[0.94,0.06],[0.95,0.05]。根据MATLAB编程计算可以得到 PR(n/N)(n=1～5)和PF(n/N)(n=1～5),求得 ER(n/N)和 EF(n/N),然后根据式(6),可以得到 EM(n/N)(n=1～5)。具体计算结果见表1。

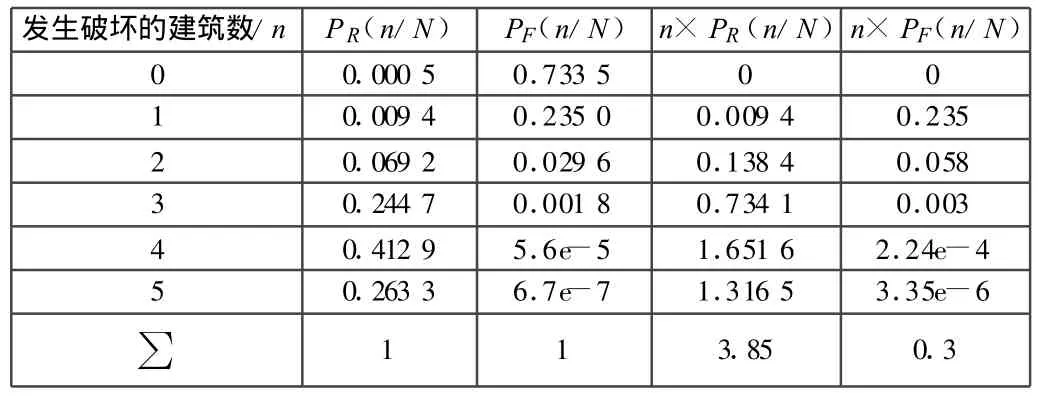
表1 有 n栋建筑发生1级,3级破坏的概率

根据表1可以得到,ER(n/N)=3.85,EF(n/N)=0.3,根据式(6),有:

同理,根据其他烈度条件下的可靠性向量,可以计算出相应其他烈度条件下的条件概率Rij,进而可以得到某种类建筑群体易损性矩阵 Mi×j。

4 结语

在可靠性向量理论基础之上,提出了可靠性矩阵,通过计算某城市或者区域抽样单体结构在不同烈度地震作用下的可靠性向量,得到结构的可靠性矩阵,即易损性矩阵。在单体结构易损性评估的基础之上,结合概率理论,形成了同类型建筑群体易损性评估方法,通过这个方法可以得到群体建筑易损性矩阵。这个方法是建立在可靠性向量理论和概率理论基础之上,计算简单方便,适用于各类结构抗震性能的快速评估,为单体建筑的抗震性能评价、抗震加固以及城市、地区的综合抗震能力评估等提供决策数据。

[1] 建设部抗震办公室.GB J11-89建筑抗震设计规范统一培训教材[M].北京:地震出版社,1992.

[2] 陈有库.城镇地区群体震害预测:快速法[D].哈尔滨:中国地震局工程力学研究所硕士学位论文,1990.

[3] 李 荷,高小旺.城市和企业地震影响灾害预测及减灾对策[M].北京:中国铁道出版社,1997.

[4] 陈德彬,高小旺.内框架建筑震害预测方法[A].第三届全国地震工程会议论文集[C].1990:1821-1826.

[5] 高小旺,钟益村.底层全框架砖房抗震能力评定和震害预测方法[A].第三届全国地震工程会议论文集[C].1990:1815-1820.

[6] 尹之潜.地震灾害及损失预测方法[M].北京:地震出版社,1996.

[7] 尹之潜.地震灾害损失预测的动态分析模型[J].自然灾害学报,1994,3(2):72-79.

[8] 陈健云,毕可为.一种适于震后快速评估的群体易损性分析方法[J].震灾防御技术,2009,4(2):174-181.