基于BP网络-突水系数理论的突水预测

贾琳瑜，陈见行，韩志婷

(中国矿业大学)

底板突水属于煤矿众多突水类型中的一种，是影响煤矿正常安全生产的重要因素之一[1]，判别底板突水有许多方法，主要包括下三带理论、突水系数法、模糊数学法、地理信息系统法、多源信息复合处理法和突水概率指数法等。其中，下三带理论法比较接近煤层底板破坏突水的情况，但测试工作比较复杂，考虑因素众多；突水概率指数法是一种考虑了多种因素对突水的综合影响而且能够反应研究区的突水规律的新方法，但需要对研究区的底层构造及水文特征要有足够的认识和研究，因此底板突水预测中，较为实用的是突水系数法。

突水系数法简单实用，但存在较多的局限性，如考虑因素较为片面而且在临界突水系数附近预测效果较差。因此，本文提出采用BP神经网络结合突水系数法对底板突水进行预测。

1 原理与方法

1.1 突水系数理论

突水系数法是指含水层中正常块段静水柱压力与隔水层厚度平衡关系变化规律的壁纸，即单位厚度隔水层所能承受的极限水柱压力之间的力学平衡条件，用公式表示为：

式中：

Ts—突水系数；

P—水压；

M—隔水层厚度。

20世纪80年代，考虑隔水层分层岩石力学性质不同，并参考了匈牙利等值隔水层厚度的概念，我国又一次对突水系数作了修正[2]，即：

式中：

Mi—隔水层底板各分层厚度；

mi—各分层等效厚度换算系数。

1.2 BP神经网络

BP神经网络一般由输入层、隐含层和输出层组成。输入层神经元的个数为输入信号的维数，隐含层神经元个数及隐含层节点的个数应视具体情况而定，输出层神经元个数为输出信号的维数[3]，具体情况见图1。

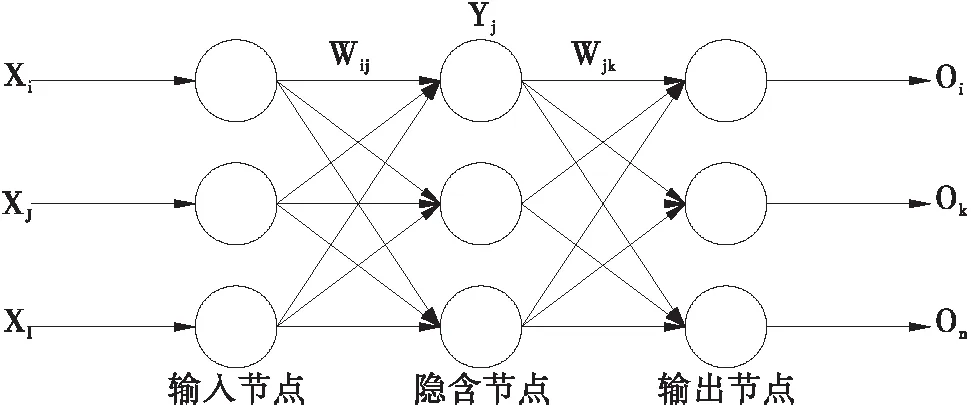
图1 BP神经网络结构示意图

输入向量为X=(xi，xj，xk)，而隐含层输出向量为Y，输出层的输出向量是O，期望输出向量为d，输入层到隐含层之间的权重用表示Wij，隐含层到输出层的向量用Wjk表示权重，则有关系：

对于输出层有：

ookp=f(netokp) (k=1,2,…,n)

对于隐含层有：

ohjp=f(nethjp) (j=1,2,…,m)

对于输入层有：

Iip=xip(i=1,2,…,l)

ΟΙip=Iip=xip

每层神经元之间的变换函数 f(x)是可微的sigmoid函数：

式中：

x—神经元的输入信号；

y—神经元的输出信号。

根据应用需要，也可以采用不同的传递函数。

1) 学习思想。BP算法采用非线性规划中的最速下降法，按误差函数的负梯度方向修改各个权值。其中，定义网络的期望输出与实际输出之差的平方和为误差函数 ，即：

式中：

yk—输出层各节点的期望值，k=1,2,…,n。

输出层各节点的期望值。

2) 调节网络连接权值。

权值修正量Δwji、Δwjk和En的负梯度关系为：

式中：

η—学习效率。

3) 调整网络神经元阀值。

同权值修正量一样，神经元阀值修正量与误差的负梯度关系为：

2 应用实例分析

2.1 样本数据

本文以某矿对工作面底板突水采集数据信息为样本进行分析，原始数据见表1。

表1 工作面底板采集信息

2.2 突水系数分析

依据突水系数理论计算6个工作面底板突水系数，计算结果见表2。

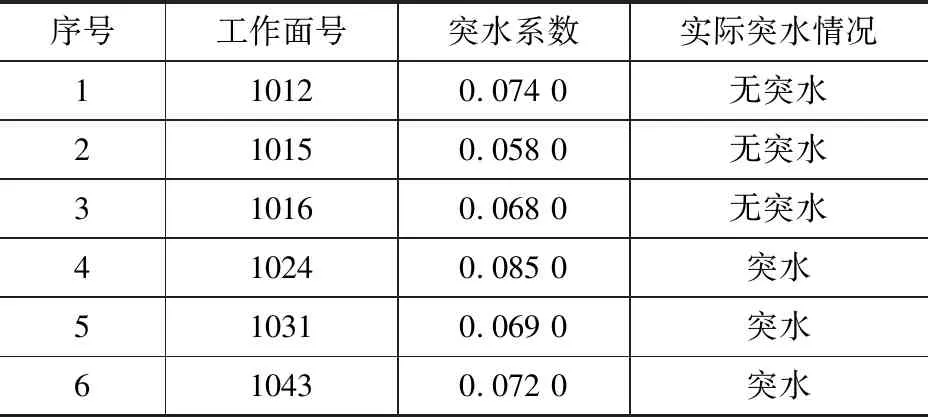
表2 突水系数计算结果

根据该矿井多年观测，确定临界突水系数为0.070。依据突水系数理论可知，当某工作面底板突水系数计算值大于0.070时，表明该面可能会发生突水事故，反之成立。

从表2可以看出，序号2即1015工作面底板突水系数为0.058 0，远小于临界突水系数0.070，预测无突水，实际回采过程中没有发生突水事故；序号4即1024工作面底板突水系数为0.085 0，远大于临界突水系数0.070，预测突水，实际回采效果发生突水，预测效果较好。

但观察剩余4组数据，发现计算得到突水系数处于临界突水系数附近，预测结果出现波动：序号3即1016工作面底板突水系数为0.068 0，预测无突水，实际没有发生突水，但序号1即1012工作面底板突水系数为0.074 0，预测突水，但实际回采没有发生突水。两工作面突水系数均处于临界突水系数附近，预测结果相反，但实际回采效果相同。序号5和序号6两组数据与之类似，说明突水系数理论在计算得到突水系数与临界突水系数相差较大时有较好的预测效果，但在临界突水系数附近确有明显波动，预测效果较差。

2.3 BP神经网络

为了提高预测精度，解决突水系数理论在临界突水系数附近的波动性问题，采用BP神经网络进行进一步预测。

1) 构建网络。底板突水状况与众多地质条件有关，如地质构造、断层的数量、底板岩层岩性及其组合特征、含水层的富水性、含水层水压、矿山压力及地应力等[4]，本文选用断层数量、富水性、隔水层承受水压及隔水层厚度4项作为影响突水的因素。

构建一个3层的BP神经网络，输入层共4个神经元，即等于影响突水的因素数目；隐含层神经元的数目采用经验公式结合逐步增长的方式确定，经验公式如下[5]：

式中：

e、p、q—分别为隐含层、输入层和输出层神经元的数目。

计算得到e=3 ，逐步增加隐含层神经元数目直至精度满足要求，最后得到隐含层共7个神经元；输出层1个神经元，即预测突水结果，输出值为0和1，分别表示底板无突水和突水。因此构建一个4×7×1 的神经网络。

2) 设置参数并进行训练。为了简化计算，采用Matlab编程进行计算，Matlab中提供了专门的神经网络工具箱(NNbox)，可以方便地进行神经网络的设计和仿真[6]。

以表1中的数据作为样本进行输入，数据输入及构建网络代码如下：

clear;

clc;

p=[3,6,4,3,16,13;

0.0210,0.031 0,0.045 0,0.900 0,0.760 0,0.500 0;

3.350 0,2.930 0,3.070 0,4.510 0,3.000 0,3.120 0;

58.000 0,63.150 0,59.160 0,66.000 0,56.450 0,54.000 0];

t=[0,0,0,1,1,1];

[pn,minp,maxp,tn,mint,maxt]=premnmx(p,t);

net=newff(minmax(pn),[7,1],{'tansig','purelin'},'traingdm');

对训练参数进行设置，具体参数见表3。

表3 训练参数

对样本数据进行训练，训练误差函数曲线见图2。

图2 训练误差函数曲线

经过4296步训练，目标函数误差达到精度要求，训练结束。输出训练结果，即：

a=[0.000 7 0.000 2 -0.000 9 1.000 0 1.000 0 1.000 0]

由于样本数据理论突水情况为：

a=[0 0 0 1 1 1]

因此，通过BP神经网络训练得到的理论结果与实际情况近似相等，表明该模型符合要求，可以用于突水的预测。

3) 预测。选取4组理论突水系数处于临界突水系数的底板监测数据见表4。

表4 预测数据样本

从表4可以看出，4组数据计算得到突水系数处于临界突水系数附近，由于突水系数理论在临界突水系数附近的波动性，因此，难以采用突水系数理论对其进行预测，下面采用训练好的BP神经网络对这4组数据进行分析，实现代码如下：

pnew=[3,7,12,10;

0.034 0,0.060 0,0.660 0,0.480 0;

3.200 0,2.970 0,3.200 0,2.980 0;

56.240 0,58.680 0,57.200 0,52.280 0];

pnewn=tramnmx(pnew,minp,maxp);

anewn=sim(net,pnewn);

anew=postmnmx(anewn,mint,maxt)

经过Matlab运算，得到输出结果为：

anew=[0.051 1 0.033 7 1.013 2 0.911 0];

可以看出，前2组输出结果近似为0，后2组输出结果近似为1，表明依据前2组数据预测无突水，后2组数据预测发生突水，与实际突水情况相符。

4) 分析。突水系数理论简便可行，被广泛用于煤矿底板突水状况的预测分析，但通过本例可以看出突水系数理论在计算得到的突水系数与临界突水系数相差较大时预测效果较好，但在临界突水系数附近确有着明显的波动性。BP神经网络考虑了更多的诱发突水的因素，通过实例分析，说明BP神经网路可以有效解决突水系数理论在临界突水系数附近的波动性问题，弥补突水系数理论的不足，可以用于临界突水系数的突水预测。

3 结论与建议

1) 应用突水系数理论对某矿6个工作面底板突水状况进行了分析，结果表明突水系数理论在计算得到的突水系数与临界突水系数相差较大时有着较好的预测效果，但在临界突水系数附近确存在着明显的波动性，预测精度较差。

2) 引入BP神经网络对临界突水系数进行预测，采用样本数据作为输入数据训练BP神经网络，用训练好的神经网络对4组突水系数理论难以判断的新数据进行了预测，预测结果与实际效果相符，表明BP神经网络在临界突水系数附近有着较好的预测效果，可以弥补突水系数理论的不足。

3) 建议对底板进行突水预测中，先采用突水系数理论对各采集样本进行突水预测，在预测结果中提取理论突水系数处于临界突水系数附近的数据作为特殊样本，以剩余的样本作学习样本进行BP神经网络训练，训练结果符合要求后，利用训练好的神经网络对特殊样本进行预测，既可以保证当理论突水系数与临界突水系数相差较大时预测效果较好，又可以保证在临界突水系数附近预测精度较高。

[1] 李永军，刘登宪. 突水系数理论在淮南矿区的应[J]. 华北科技学院学报，2008(4)：26-28.

[2] 段水云. 煤层底板突水系数计算公式的探讨[J]. 水文地质工程，2003(1)：97-100.

[3] 敬忠良. 神经网络跟踪理论及应用[M]. 北京：国防工业出版社，1995：21-23.

[4] 李 涛，李文平，高颖,等. 突水系数理论在桃园矿区的实践[J]. 矿业安全与环保，2010(2)：26-28.

[5] 余晓红. BP神经网络的MATLAB 编程实现及讨论[J]. 浙江交通职业技术学院学报，2007(12)：45-48.

[6] 桂现才. BP神经网络在MATLAB上的实现与应用[J]. 湛江师范学院学报，2004(3)：79-83.

收稿日期 2010-07-22