平面4N体问题的扭转正多边形套周期解
2010-06-08苏霞
苏 霞
(淮阴工学院数理学院,江苏淮安 223003)
0 引言
天体力学是一门古老的学科,是天文学的一个重要分支,但又同数学和力学有着千丝万缕的联系。天体力学是天文学和力学之间的交叉学科,它运用力学规律来研究天体的运动和形状。天体内部和天体相互之间的万有引力是决定天体运动和形状的主要因素,它以万有引力定律为基础。虽然已发现万有引力定律与某些观测事实发生矛盾,而用爱因斯坦的广义相对论却能对这些事实作出更好的解释,但对天体力学的绝大多数课题来说,相对论效应并不明显。因此,在天体力学中只是对于某些特殊问题才需要应用广义相对论和其他引力理论。天体力学以数学为研究手段。它的研究内容包括二体问题、三体问题、多体问题、摄动理论、天体形状和自转理论,以及有关天体运动的定性理论和数值方法。天体力学还和天体测量学、星系力学、天体动力演化论、天体物理学等密切相关。多体问题又叫N体问题,是研究N个质点在万有引力作用下的运动。在N=2时为二体问题,这个问题是天体力学的基本问题之一,已得到完全解决。在N=3时为三体问题,这个问题难度较高,多年来进展甚慢,仍未得到解决,正用分析方法、数值方法和定性方法进行研究。还有许多人致力于一些特殊问题的研究,如三体问题的积分、限制性三体问题等。对于其他多体问题,主要研究运动的一般特性。在现代天体力学的研究中,多体问题是一个重要领域,这是天体力学同一般力学和应用数学之间的共同研究领域。牛顿多体问题主要研究在牛顿运动定律和万有引力作用下,天体的运动规律。
1 问题的提出
对于N≥2的平面N体问题的运动方程可以写成

这里zk是质量mk∈R+的质点在惯性坐标系中的复坐标。
在文献[2]和[4]中,作者研究了平面N体问题的正多边形解和平面2N体问题的正多边形套周期解。本文研究4N体问题的扭转正多边形套周期解。
假设4N个天体位于圆心在坐标原点的三个同心圆上,且每个圆上的质点构成一个正多边形,它们的边数分别为N,2N,N。

假设质点mk∈R+位于 ρ2k(k=1,2,…,N),m'k∈R+位于 ρ'k(k=1,2,…,N),m''k∈R+位于 ρ''k(k=1,2,…,N)。令质点系的质心

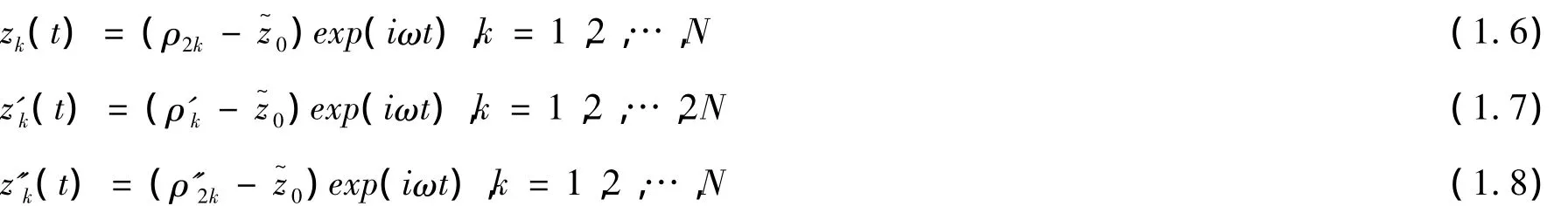
方程(1.1)可以改写为

2 主要引理
定义2.1 若N×N矩阵A=(ai,j)满足

则称A是一个循环矩阵。
引理2.1 如果A和B是循环矩阵,则A+B,A-B,A·B也是循环矩阵,且AB=BA。
引理2.2 设A=(ai,j)是N×N循环矩阵,则A的特征值λk和特征向量vk是

引理2.3 设A和B是循环矩阵,λk(A)和λk(B)是A和B的特征值,则A+B,A-B,A·B的特征值分别是 λk(A)+λk(B),λk(A)-λk(B),λk(A)·λk(B)。

3 问题的解决
zk(t),z'k(t),z"k(t)是方程(1.9)、(1.10)、(1.11)的解的充要条件是
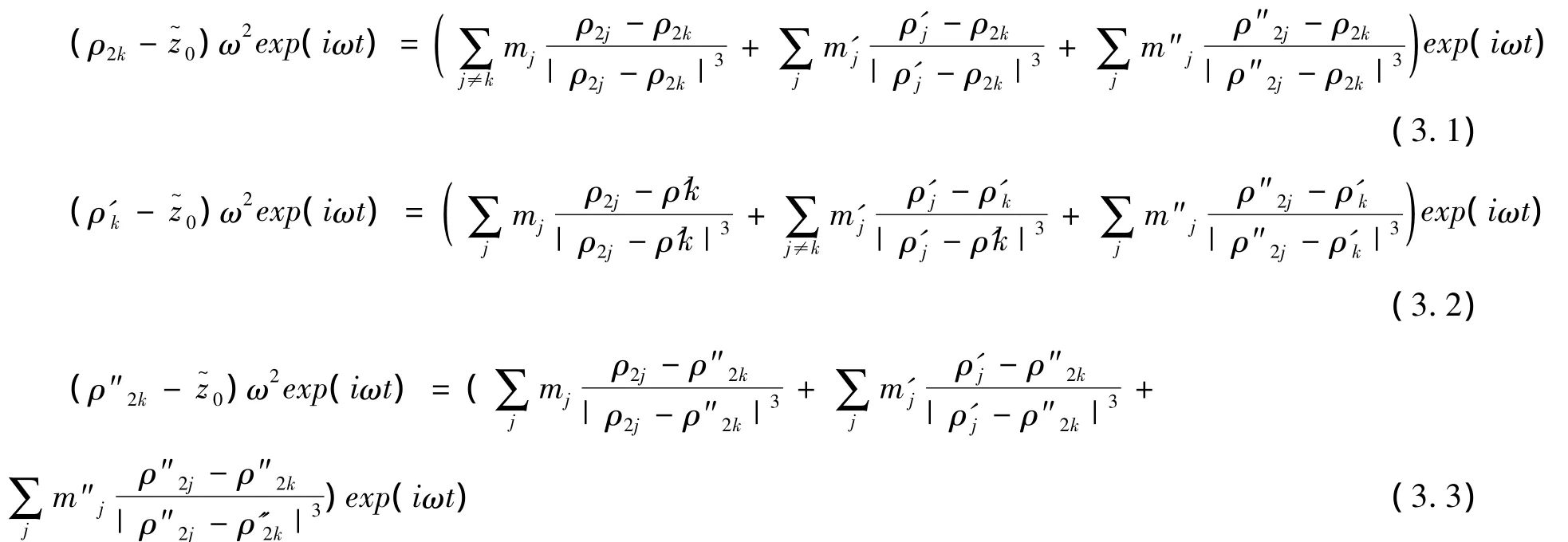
或者等价地表达为:


注意式(3.1)到式(3.9)是可逆的。

设M1=(m1,…,mN)T,M2=(m'1,…,m'2N-1)T,M3=(m'2,…m'2N)T,M4=(m''1,…m''N)T,则式(3.7),式(3.8),式(3.9)成立的充分必要条件是方程组

有一个正解,等价于

有正解,其中

注意到方程(3.11)有正解,等价于Q对应于0特征值的正实特征向量。
由引理2.3得

因此,对于某个1≤k≤N,

成立,即
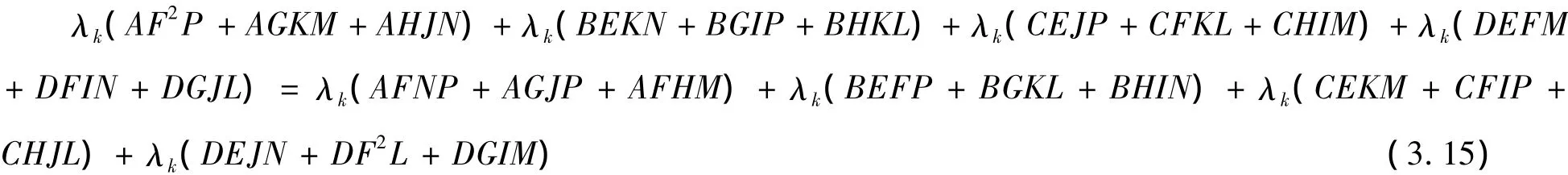
由引理2.2 及 2.4,我们有 λk,因此有
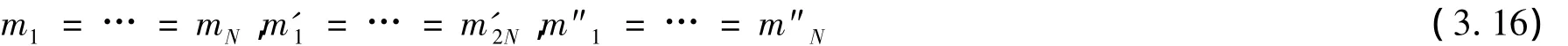
且ω满足:

其中


4 结论
由上述讨论,我们有如下结论:
定理 1 当N≥2 时,式(1.6),式(1.7),式(1.8)是方程组(1.9),(1.10),(1.11)的解,则 ω 满足
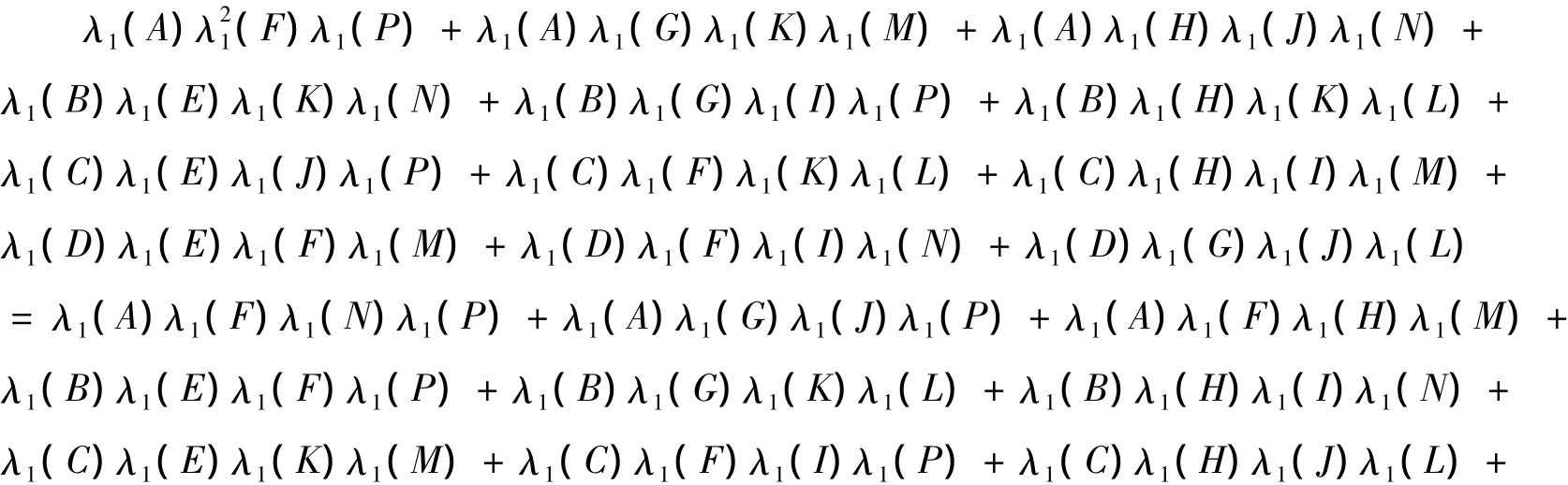
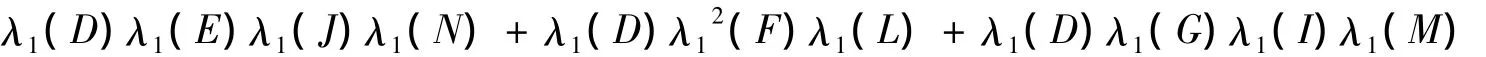
定理2 当N≥2 时,(1.6),(1.7),(1.8)是方程(1.9)(1.10)(1.11)的解的充分必要条件是
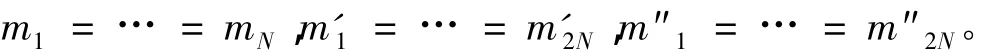
[1]Abraham R,Marsden J.Foundations of Mechanics[M].London:Benjamin/Cummings,1978.
[2]L M Perko,E Lwalter.Regular polygon solutions of N-body problem[J].Proc AMS,1985,94:301-309.
[3]Moeckel R.On central configurations[J].Math,1990,205:499-517.
[4]Meyer K,Hall G.Introductions to Hamilitonian Systems and n-body problems[M].Berlin:Springer,1992.
[5]S Q Zhang,Q Zhou.Periodic solutions for planar 2N-body problems[J].Proc AMS,2002,131:2161-2170.
[6]程云鹏.矩阵论[M].西安:西北工业大学出版社,2001.
[7]陈剑.平面3N体问题的中心构型[J].绵阳师范学院学报,2008,27(5):8-12.
[8]陈静.一类平面对称五体问题的中心构型[J].扬州职业大学学报,2008,12(4):40-43.
[9]刘文中,徐玢,王欢,等.N-体问题的“蜂窝型”中心构型[J].北京师范大学学报:自然科学版,2006,42(6):576-578.
[10]刘学飞,姜友谊.一类平面五体中心构型[J].重庆大学学报:自然科学版,2004,27(3):65-68.
[11]朱长荣,罗广萍.N+1-体问题的空间和平面中心构型[J].重庆大学学报:自然科学版,2007,30(9):96-98.
[12]龙以明,孙善忠,张世清.中心构型和线性方程组[J].南开大学学报:自然科学版,2002,35(4):26-34.
[13]汤建良.关于4-体问题中心构型的一点研究[J].系统科学与数学,2006,26(6):647-650.
[14]苏霞,温书.四体问题的平行四边形中心构型[J].淮阴工学院学报,2006,15(5):15-19.
