水力半径简算方法探讨

胡兰秋，李秀荣

（1.绥滨县水务局，黑龙江绥滨 156200;2.牡丹江市水利勘测设计研究院，黑龙江牡丹江 157000）

1 概述

在洪水调查及天然河道水面曲线计算中，计算洪峰流量、水文站糙率和河道设计洪水位时，一般常用曼宁公式：C公式中水力半径R的准确与否将直接影响计算的精度。对于水力半径的计算，由于精算法比较繁琐，目前多采用简化方法，有时为了计算简便常用计算断面的平均水深代替水力半径推求糙率值和断面设计洪水位等，水力半径如选用不当，会严重影响计算成果的精度。究竟简化方法是否可以采用?各种简化方法在什么条件下选用比较合适?本文就上述问题进行简要的分析论述，仅供参考。

2 水力半径简算方法概述

水力半径计算公式为：

式中：A为过水断面面积，m2;x为湿周，m;R为水力半径，m。

由（1）式可以看出，水力半径R精算与简算的区别主要在于湿周X的精算与简算。目前常用的简算方法主要有3种，即：

式中：B为断面不同水深时水面宽度，m;h0为断面平均水深，m。

分别选取矩形、梯形、三角形、抛物线形、天然河道断面共5种类型河床（包括宽浅、窄深式）计算水力半径的精算值R精和3种简算值及相对误差，建立R精～R简相对误差关系曲线。详见表1～表5和图1～图10。

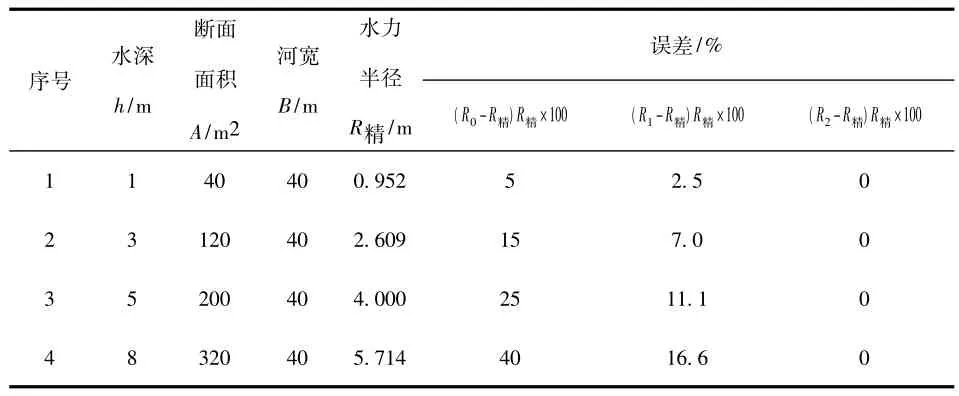
表1 矩形河床R精～R简不同算法比较计算表

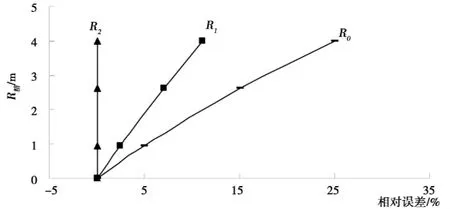
图1 矩形河床R精～R简相对误差关系曲线图

表2 抛物线形河床R精～R简不同算法比较计算表

图3 抛物线形河床R精～R简相对误差关系曲线图

图4 抛物线形河床断面图

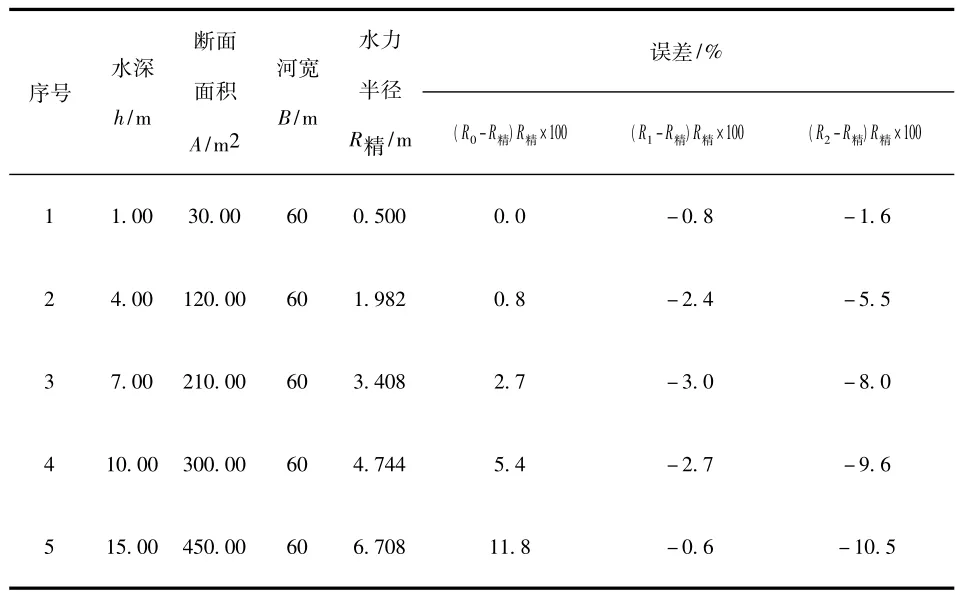
表3 三角形河床R精～R简不同算法比较计算表

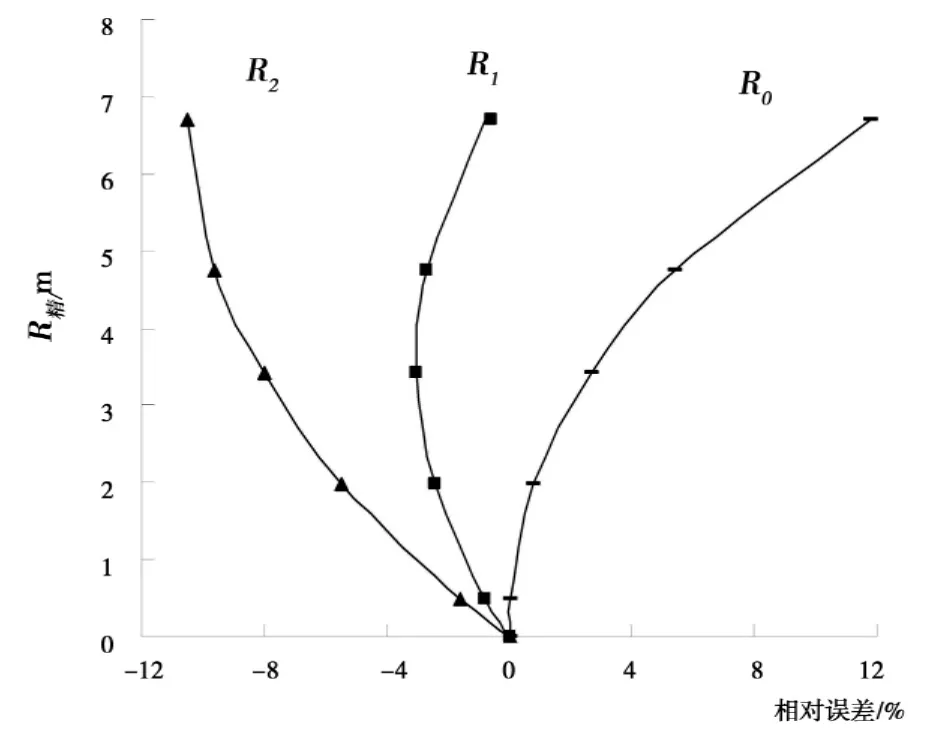
图5 三角形河床R精～R简相对误差关系曲线图

图6 三角形河床断面图

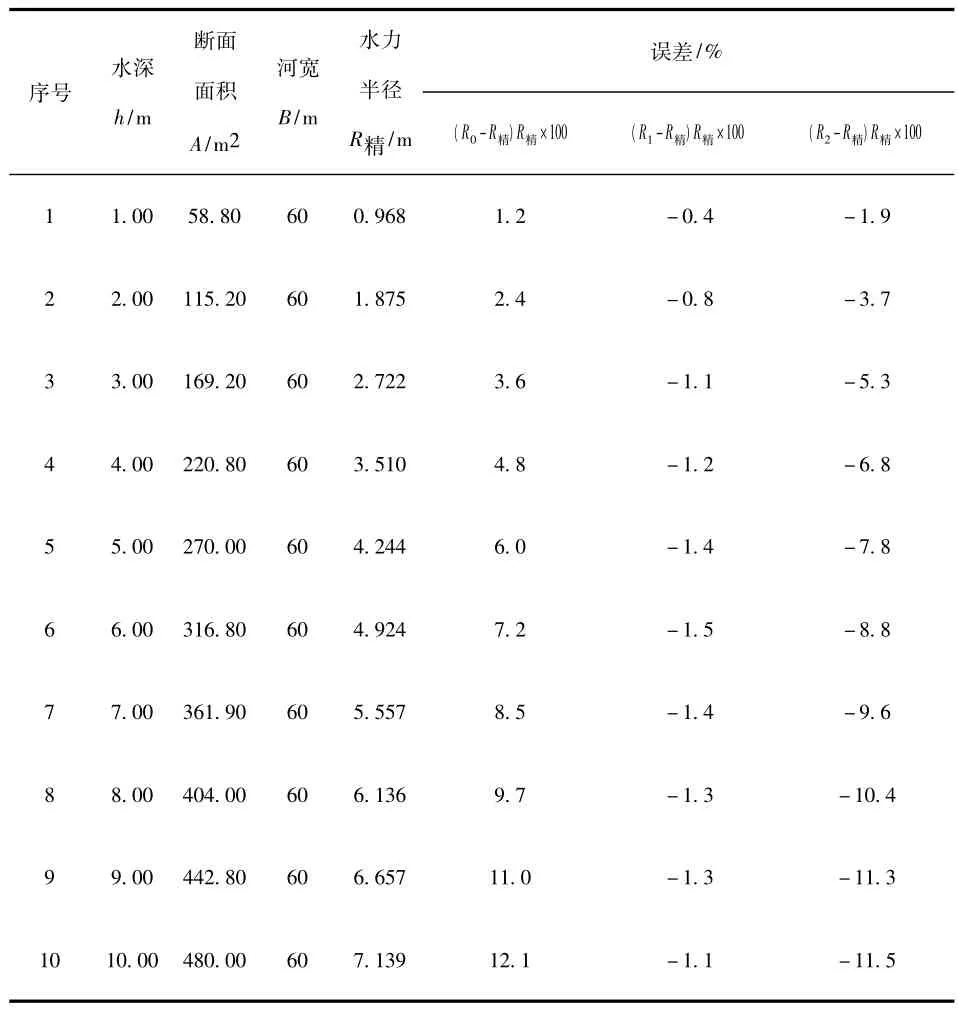
表4 梯形河床R精～R简不同算法比较计算表

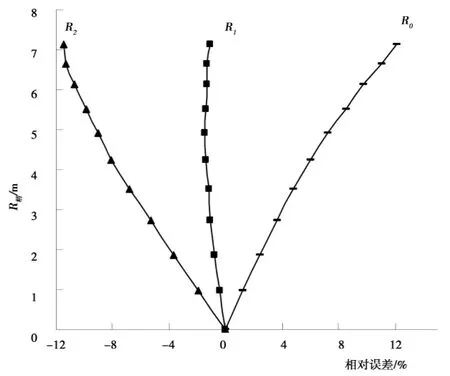
图7 梯形河床R精～R简相对误差关系曲线图

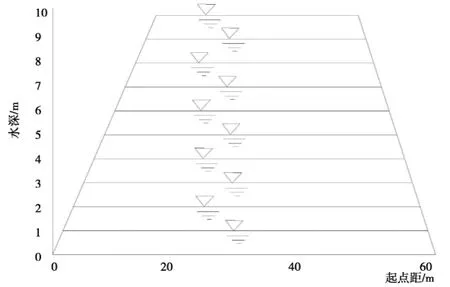
图8 梯形河床断面图

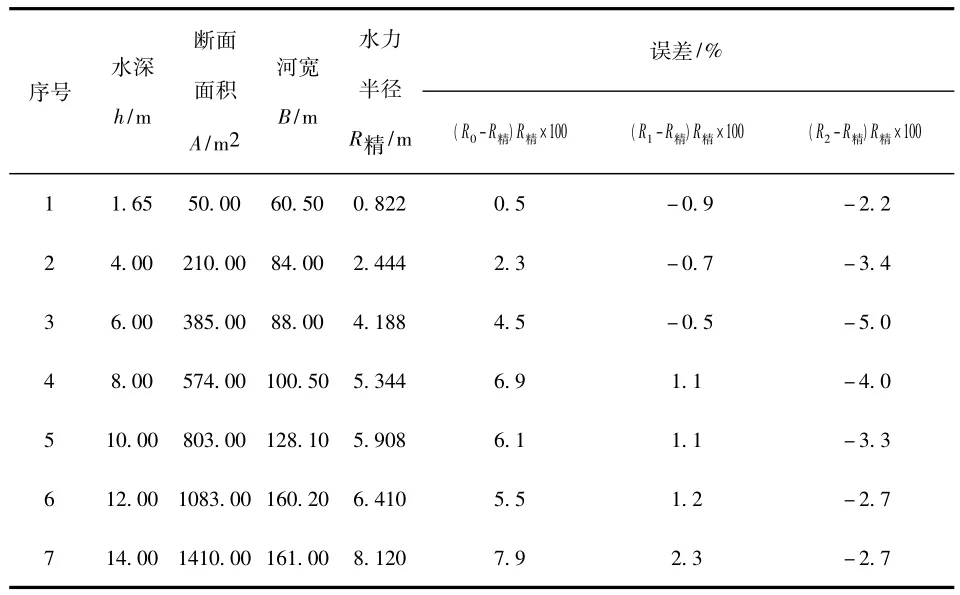
表5 天然河床R精～R简不同算法比较计算表

3 成果分析

从图中可以看出：

1）R简的误差与 R的大小成正比，当 h0＜2 m时，R简≈R精。

2）宽浅式河床，当B/h0＞20时，3种简算值均接近精算值。

3）矩形断面的湿周 x精=h0=B+2h0，故 R2=R精。R1、R0的相对误差分别在2.5% ～16.6%、5.0% ～40%。

4）除矩形断面外，其他各种河床都是R1≈R精，其误差仅为-3.5% ～2.3%。以R0作水力半径，其值偏大，相对误差从0.4% ～12.1%，以R2作水力半径，其值偏小，相对误差从-1.6%～-11.5%。

图9 天然河床R精～R简相对误差关系曲线图

图10 天然河床断面图

4 结语

根据上述分析，对选用简算法计算水力半径提出如下4点建议，供参考：

1）除矩形断面外，不采用x=B+2h0计算湿周。

2）除B/h0＞20外，不采用平均水深代替水力半径。

3）一般情况下，用x=B+h0计算湿周;当B/h0＞20时，可以用平均水深代替水力半径;当河床为矩形或近似矩形时，用x=B+2h0计算湿周。

4）水文站计算糙率时，水力半径最好采用精算法。

[1]吴持恭.水力学[M].北京：高等教育出版社，1993.

[2]袁作新，等.工程水文及水利计算[M].北京：水利出版社，1980.