输电塔-线体系覆冰作用非线性分析
2010-06-08晏致涛刘操兰李正良汪之松
晏致涛,刘操兰,李正良,汪之松
(1.重庆大学 土木工程学院,重庆 400045;2.中国电力科学研究院,北京 100192)
输电塔-线体系是由高耸的杆塔结构和导线连接组成的一种高柔结构,在高海拔、覆冰等恶劣条件下,存在大悬臂横担引起的几何非线性大变形以及导线的脱冰、断线等引起的导线跳跃和对输电塔的冲击作用等问题。由于输电塔的高耸、柔性性质,几何非线性影响不容忽视[1-2]。
输电塔塔身主要角柱一般为连续受压压杆,存在杆件的次弯矩作用,即存在 P-Δ效应。El-Ghazalyt H A[3]以KUWAIT地区的1个输电塔为例,采用ANSYS和STAAD-III计算软件包建立了1个二维耐张塔的计算模型,分析了风荷载下塔受力的几何非线性影响。Da Silva[4]对目前输电塔设计的模型进行了分析比较,重点分析了纯桁架模型和梁-杆模型之间的差别。Prasad Rao[5]针对典型的等肢角钢塔进行了分析,重点考察了风荷载作用下结构几何非线性的影响。邓洪州[6]、Ji-Hun Park[7]通过试验研究了梁单元和杆单元模型的区别,分析了梁单元模型中次应力的影响。Roy S[8]也从理论上分析了梁单元中次应力的影响。
上述相关研究基本上是对单塔的几何非线性进行分析,并且没有考虑塔身扭转产生的荷载非线性。
越来越多的研究关注输电塔—导线体系的整体耦合受力分析。Ronaldo C[9]、Kudzys[10]分析了风荷载作用下输电塔的动力特性和稳定性。Wahba[11]对拉线天线塔进行了数值模拟,分析了拉线塔—线整体模型与单塔模型在风荷载、覆冰荷载下的力学性能的差别。胡松[12]、李宏男[13]、梁峰[14]等分别讨论了输电塔-线体系在风荷载、地震荷载下的动力特性与建模。上述研究大都集中在整体力学性能方面,基本没有涉及铁塔非线性内容,尤其是荷载非线性的影响没有考虑。
以下将建立较准确的输电塔-线体系分析模型,考虑输电塔、导(地)线以及绝缘子的非线性力学特性,实现体系在各种覆冰工况下考虑几何非线性的力学分析,讨论不均匀覆冰引起塔身扭转的非线性影响。
1 输电塔-线体系力学模型
1.1 输电塔力学模型
以往的研究表明,由于杆件在节点连接处刚度增强,次应力问题在设计中应该考虑,尤其是4根角柱和大悬臂的主要杆件,其实际上就是连续梁结构,按梁单元进行有限元计算比按杆单元计算的结果与试验值更为接近。本次研究的输电塔结构构件主要为单边连接等肢角钢,在进行非线性静力分析时,对主要的拉压杆件如角柱、悬臂上下弦采用三维空间梁单元模型,对主要的“X”撑、“K”撑等也采用刚性节点,并考虑连接偏心的影响根据现行规范对横向支撑进行刚度上的修正[5]。次级的小支撑在分析中内力很小,往往通过构造决定,采用轴向受力模型。
1.2 导线力学模型
对于导(地)线索单元,已有许多研究表明采用悬链线模型计算输电线是精确的[15],因此,采用悬链线单元模拟导(地)线。空间悬链线刚度是一个隐式表达式,可通过迭代求得。由于输电塔线体系是一个多跨体系,在分析时,往往只取出其中的几跨。因此,确定相邻导线的轴向刚度和侧向刚度是相当有必要的。为简便起见,在边界处相邻跨的导线采用抛物线模型,这样,便可以得到导线刚度的显示表达式。导线的轴向刚度为
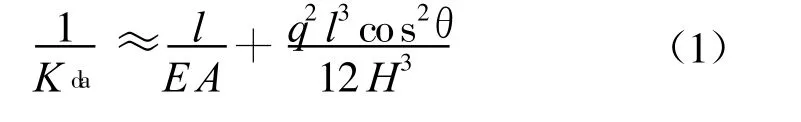
其中,E为导线弹性模量;A为导线的面积;H为导线的沿弦向张力;l为导线的水平档距;θ为风荷载与导线之间的夹角。若索只受重力作用,则q为分布重度;若索同时还受侧向风荷载作用,则上式中还需要添加风荷载的贡献,则q为风荷载与自重荷载的合力。
导线侧向受力分析模型如图1所示。水平虚线表示变形前的导线,实线表示变形后的位置;U为导线侧向位移;F为侧向摆动力;θ1与θ2分别为导线与原位行的夹角。根据静力平衡条件可以得到导线侧向刚度系数

其中,L1、L2分别为相邻2跨长度;H1和H2分别为相邻2跨导线水平张力。
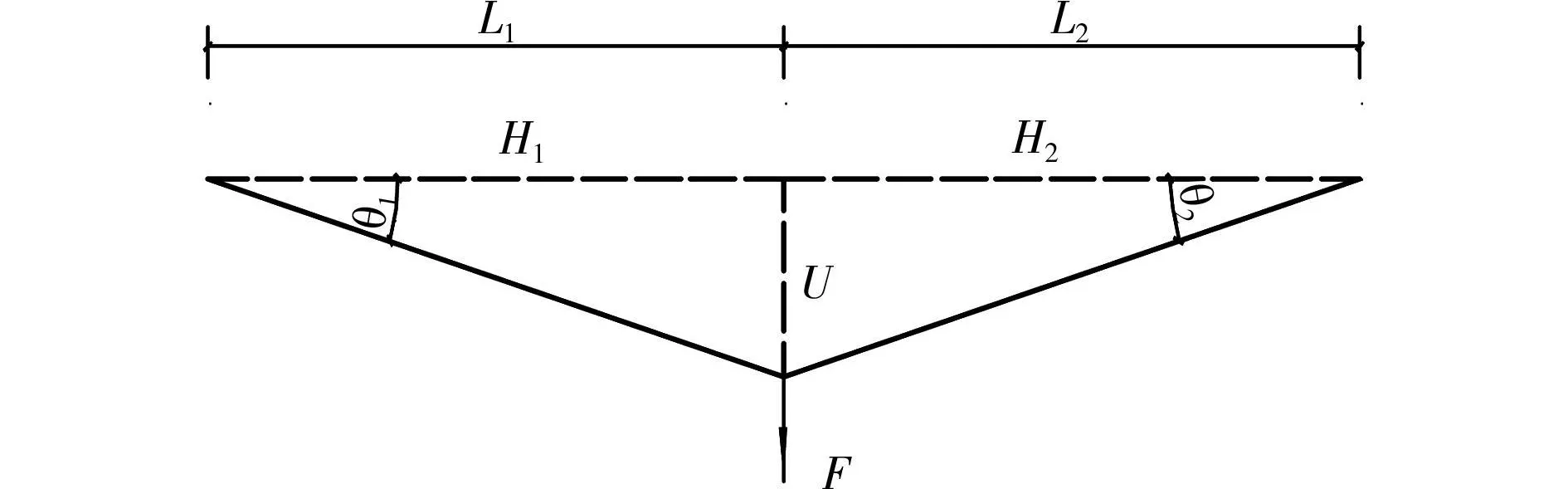
图1 导线侧向的受力分析
1.3 绝缘子力学模型
输电塔的绝缘子一般有单串和“V”串 2种形式。单串绝缘子主要考虑沿线向和侧向2个方向的摆动刚度,“V”串绝缘子沿导线向刚度为2串绝缘子之和,侧向刚度可以根据2串绝缘子的轴向刚度和夹角确定。以下主要介绍单串绝缘子沿2个方向的摆动刚度求解,忽略悬挂绝缘子串的拉伸变形,假定绝缘子轴向为完全刚性。以沿导线向(X向)摆动刚度系数为例,典型的变位后的绝缘子串形状如图2所示,图中水平荷载Fx主要是由于导线的自重、覆冰以及风荷载引起。根据静力平衡,可以得到刚度系数
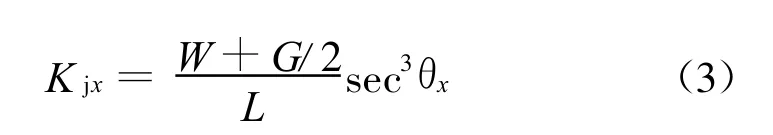
其中,L为绝缘子串长度;G为绝缘子自重;W为绝缘子底部作用导线自重及覆冰等垂直荷载;θx为绝缘子串在xz平面上的投影与z轴的夹角。K jx为悬挂绝缘子串x向摆动切线刚度,y向摆动刚度可以进行类似推导。可见绝缘子的刚度系数和自重、投影长度以及摆动角度、导线上的自重及覆冰、风荷载(引起W 的变化)等均有关,与变形呈强非线性关系,现有商用软件均未有合适单元可以采用,必须自编程序实现。
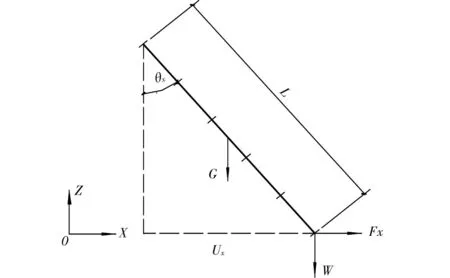
图2 绝缘子的受力分析
1.4 边界条件
在分别求得了导线、绝缘子、输电塔的刚度,输电塔-线体系边界处的竖向刚度、横向刚度可以通过对直线塔的相邻跨刚度集成得到(直到耐张塔)。定义输电塔的刚度为K t,绝缘子的刚度为K j,导线的刚度为K d。由于输电塔与绝缘子属于串联关系,和导线则属于并联关系,则总的刚度矩阵有如下表达式

2 覆冰作用下静力非线性计算
根据上述分析过程,以正在修建的向家坝-上海±800 kV特高压直流输电线路为例(如图3)建立了一个考虑边界条件的输电塔线体系简化分析模型,进行覆冰荷载下的塔线耦联体系静力非线性分析。该工程是目前世界上最高电压等级的示范工程,起自向家坝换流站,止于上海换流站。该工程参数为(数据来自西南电力设计院):直线跨越塔呼高50.6 m,全高69m,跨度450m。采用耐-直-直-直-耐体系。水平档距为450 m,中间输电塔为直线塔。地线采用 LBGJ-210-20AC,截面 209.85 mm2,直径 18.75mm,线重 14.022 N/m,最大覆冰30mm,覆冰最大张力为77 610 N。导线采用A 3/S1A-651/45,分裂数为6,截面面积为 696 mm2,导线自重为21.040 6 N/m,导线最大张力为484 420 N。单串导线绝缘子为4 500 kg,地线绝缘子重量为100 kg。导线绝缘子为“V”串,地线绝缘子为单串。
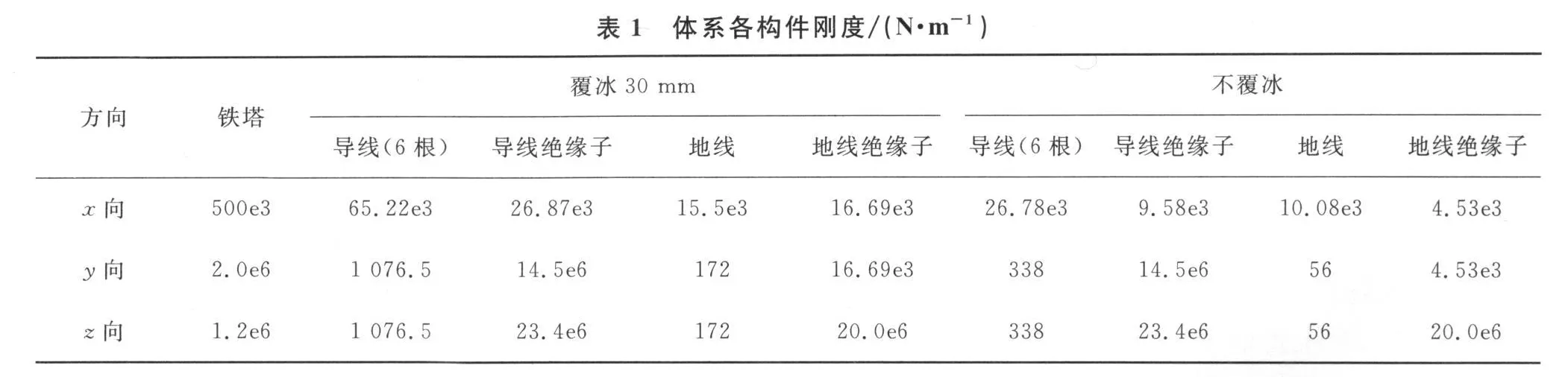
相邻跨导(地)线、输电塔以及绝缘子的边界条件用弹簧模拟,经计算,地线连接处边界弹簧刚度分别为 30.24 kN/m 、16.72 kN/m 、1 130 kN/m;导线连接处边界弹簧刚度分别为76.34 kN/m、1 760 kN/m、1 140 kN/m。体系各构件刚度如表1所示,其中X向为顺线向(铁塔为大悬臂导线悬挂点处),Y向为侧向,Z向为竖向。可以看出,不论是覆冰还是不覆冰状态,铁塔、导(地)线以及绝缘子体系耦联作用是显著的。

图3 输电塔线体系分析模型
对7种覆冰工况进行了静力非线性分析,其中工况1:导(地)线不覆冰、风速 27 m/s;工况 2:导(地)线覆冰厚度 30 mm,风速 15 m/s;工况 3:导(地)线覆过载冰,覆冰厚度45 mm,风速15 m/s;工况4:不均匀覆冰I(第1跨前导线、第 2跨后导线覆冰30mm,其余不覆冰),风速15m/s;工况5:不均匀覆冰II(第1跨前导线、第2跨后导线覆冰45mm,其余覆冰30mm),风速15 m/s;工况6:不均匀覆冰 I(第1跨前导线、第2跨后导线覆冰30 mm,其余不覆冰),风速为0;工况7:不均匀覆冰I(1跨前导线、2跨后导线覆冰30mm,其余不覆冰),风速30m/s。前7种工况为实际工程设计中需要考虑的工况,后2种工况主要是用来和工况4比较。
分别计算了体系在线性及非线性分析工况下的内力,计算结果表明,输电塔构件的内力受几何非线性的影响和其拉压状态有关,考虑几何非线性后,受拉构件及受压较小构件内力有适度降低,但以受压为主的构件由于荷载非线性比较明显,内力有所增大。在5种工况下,弹性支座处的反力和大部分受拉杆件、导(地)线的内力等在考虑了几何非线性的影响后均变小。“V”串绝缘子中受拉一侧内力变小,受压一侧增大。5种工况下输电塔的支座反力如表2,由于结构对称,因此只取了2 688、2 705、2 720等几个点分析(节点编号见图3)。表中Fx、分别表示全局坐标系下结构在x、y、z方向的力和力矩。结果表明,工况 1、工况 2、工况3的内力增大不是非常明显,工况4-工况7的P-Δ效应比较明显。工况4中主要受压支座节点2 688和2 720最大竖向反力(Fz方向)分别增大6.7%和4.1%,最大弯矩(M x方向)增大11.6%和11.8%。工况5节点2 688及2 720轴向反力分别增大15.5%、4.1%,弯矩分别增大16.2%和17.9%。

表2 输电塔支座节点反力/N
表3为上述工况中前5种工况下分别考虑几何非线性和线性工况下计算的输电塔横担底部最大受压弦杆的内力(单元号见图 3)。表中 P、V2、V3、T、分别表示局部坐标系下结构的最大轴力、剪力、扭矩和弯矩。结果表明,工况1、工况 2、工况 3、杆件内力都变化不大,但对于工况4和工况5,其P-Δ效应比较明显。工况4中单元91和单元115的轴力最大分别增大9.4%和8.7%,弯矩分别增大6.7%和16.5%。工况5中单元91和单元115的轴力最大分别增大4.0%和4.2%。

表3 输电塔大悬臂下端单元内力
3 荷载非线性分析
从上述计算中可以看出,前3种工况由于结构和荷载对称,铁塔支座底部和大悬臂底部只受到侧向风荷载的作用,在考虑几何非线性分析之后,结构的内力变化相差不大,一般较线性分析结果偏小。当考虑不均匀覆冰工况(工况4-工况7)之后,铁塔两侧导线的张力不平衡,从而产生对铁塔的扭转效应。一段底部铁塔在扭矩T作用下的变形如图4所示,从变形图可见,扭矩使铁塔产生扭转,主要角柱产生侧向偏移,因此在压力 P作用下产生附加弯矩,从而导致荷载非线性。
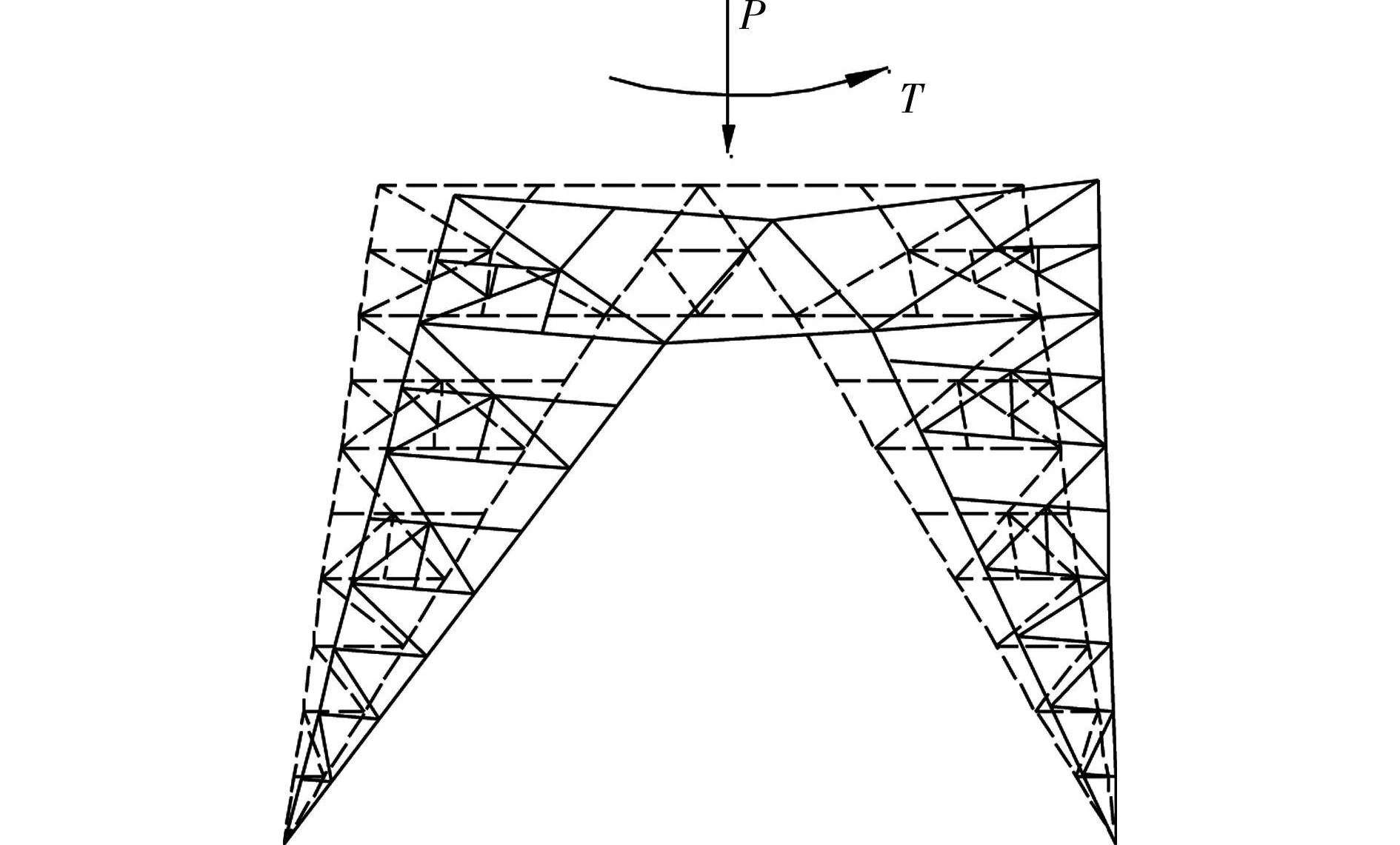
图4 输电塔扭转变形示意图
没有风荷载作用下,铁塔受到仅有扭转作用和轴向力作用,铁塔受力杆件产生侧移,从而产生次弯矩。经反复计算,结果表明,主材次弯矩的影响可以参考现行钢结构设计规范[16]建议的公式近似简化估算。
若输电塔-线体系受到风荷载的作用,由于导线覆冰致使导线的迎风面积发生改变,铁塔两侧导线的风荷载也会引起导线张力不一致,从而使铁塔产生扭转效应和侧弯效应。在轴力、扭距和弯矩作用下,在考虑几何非线性时铁塔主要杆件的轴力、剪力和弯矩均发生明显的改变,有些杆件增大,有些杆件变小。对工况4、工况6、工况7的计算结果比较表明,在不均匀覆冰工况下,风荷载会增大扭转效用的非线性影响,除弯矩外,轴力、剪力也会有一定的增加,变化规律较复杂,应该采用精确的几何非线性力学模型分析。
4 结 论
采用输电塔-线体系的简化模型分析了7种覆冰工况下结构的内力和变形情况。分析表明,在结构荷载和体型均为对称的工况下,扭转效应较小,从而导致荷载非线性不是很显著,多数构件按线性计算结果较非线性结果大,计算结果偏于保守。若导线受到不均匀覆冰作用,由于导线不平衡张力对铁塔的扭转作用,主要受压支座节点和最大悬臂处单元的轴向压力和弯矩都有较明显的P-Δ效应。另外,在不均匀覆冰工况下,导(地)线上风荷载也会增大扭转效用的非线性影响,弯矩、轴力、剪力均会产生一定的改变。算例表明,考虑几何非线性后,当风速为15 m/s以及导线不均匀覆冰II(第1跨前导线、第2跨后导线覆冰45mm,其余覆冰30mm)时,支座节点轴向反力可增大 15.5%,弯矩可增大17.9%。可见,与一般结构考虑几何非线性后会减小结构响应不同,在不对称覆冰及风荷载下,考虑几何非线性会增大输电塔-线体系内力响应,在工程设计中应该采用精确的几何非线性力学模型分析这种不利影响。
[1]李正,杨靖波,韩军科,等.2008年输电线路冰灾倒塔原因分析[J].电网技术.2009,33(2):31-35.LIZHENG,YANG JING-BO,HAN JUN-KE,et a l.Analysis on transm ission tow er topp ling caused by icing disaster in 2008[J].Pow er System Techno logy.2009,33(2):31-35.
[2]LI HONG-NAN,BA I HA I-FENG.High-voltage transm ission Tower-line system sub jected to disaster loads[J].Progress in Natural Science,2006,16(9):899-911.
[3]EL-GHAZA LYT H A,AL-KHA IATZ H A.Analysis and design of guyed transm ission towers-case study in KUWA IT[J].Com puters&Structure,1998,55(3):413-431.
[4]DA SILVA JG S,DA S P C G,DE ANDRADE SA L,et al.Structural assessment of current steel design models for transm ission and telecommunication towers[J].Journal o f Constructional Steel Research.2005,61(8):1108-1134.
[5]PRASAD RAO N,KALYANARAM AN V.Non-linear behaviour of lattice panel of angle Tow ers[J].Journal of Constructional Steel Research.2001,57(12):1337-1357.
[6]邓洪洲,陈晓明,屠海明,等.江阴大跨越输电塔模型试验研究[J].建筑结构学报,2001,22(12):31-35..DENG HONG-ZHOU,CHEN XIAO-M ING,TU HAIM ING,et al.Experimental study on model of Jiangyin long span transm ission tower[J].Journalof Building Structures.2001,22(12):3l-35.
[7]PARK JI-HUN,MOON BYOUNG-WOOK,M IN KYUNG-WON,et al.Cyclic loading test o f frictiontype reinforcing members upgrading wind-resistant performance of transmission tow ers[J].Engineering Structures.2007,29(11):3185-3196.
[8]ROY S,FANG S-J,ROSSOW EC.Secondary stresses on transmission tow er structures[J].Journal of Energy Engineering.1984,110(2):157-171.
[9]RONALDO C BATTISTAA, ROSANGELA S RODRIGUESA,et al.Dynam ic behavior and stability of transmission line tow ers under w ind forces[J].Journal of Wind Engineering and Industrial Aerodynam ics.2003,91(8):1051-1067.
[10]AN TANAS KUDZYS.Safety of pow er transm ission line structures under w ind and ice storms[J].Engineering Struc tures.2006,28(5):682-689.
[11]WAHBA Y M F,MADUGULA M K S,MONFORTON G R.Evaluation of non-linear analysis of guyed antenna tow ers[J].Computers&Structures.1998,68(1-3):207-212.
[12]胡松.大跨越输电线路的风振反应分析及振动控制研究[D].上海:同济大学土木工程学院.1999.12.
[13]李宏男,胡大柱,黄连状.地震作用下输电塔体系塑性极限状态分析[J].中国电机工程学报.2006,26(24):192-199.LI HONG-NAN,HU DA-ZHU,HUANG LIANZHUANG.Plastic lim it analysis of the transm ission tow er system subjected to earthquake action[J].Proceedings o f the CSEE.2006,26(24):192-199.
[14]梁峰,李黎,尹鹏.大跨越输电塔-线体系数值分析模型的研究[J],振动与冲击,2007,26(2):61-65.LIANG FENG,LI LI,Y IN PENG.Numericalanalysis of pow er transm ission tower-linemodel[J].vibration and shock,2007,26(2):61-65.
[15]SOROKINA S V,REGA G,GOULOIS A M.On modelling and linear vibrations of arbitrarily sagged inclined cab les in a quiescent viscous f luid[J].Journal of Fluids and Structures,2007,23(7):1077-1092.
[16]GB50017-2003钢结构设计规范[S].北京:中国计划出版社.2003.
