基于压缩传感的图像哈希水印算法研究*
2010-06-05张德丰马子龙
周 燕,张德丰,马子龙
(1.佛山科学技术学院计算机系,广东 佛山 528000;2.哈尔滨工业大学电子工程系,黑龙江 哈尔滨 150001)
近年来,由Donoho,Candes[1]及华裔科学家Tao等人提出的压缩传感理论,受到了广泛关注。该理论利用信号的稀疏性先验知识,通过合适的优化算法,可由少量的测量值重建原始信号。这些测量值代表了图像的内容特征,利用该特性可由测量值生成数字水印[2-3]。本文提出了一种基于压缩传感的图像哈希水印算法,首先对原始图像进行压缩传感随机投影,得到图像的压缩测量值,然后利用HMAC(Hash-based Message Authentication Code,基于哈希的消息认证码)算法生成哈希水印并嵌入到原始图像中;认证时,首先提取认证图像中的水印,经过非对称解密,得到代表原始图像的摘要;然后对认证图像进行压缩传感随机投影,利用HMAC算法生成代表认证图像的摘要;最后通过比较原始图像和认证图像的摘要,实现图像认证和篡改检测。
1 基于压缩传感的水印模型及算法实现
1.1 压缩传感理论分析
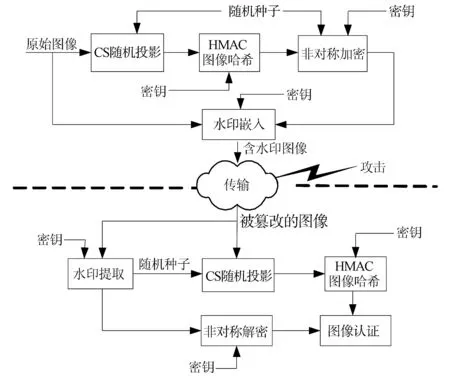
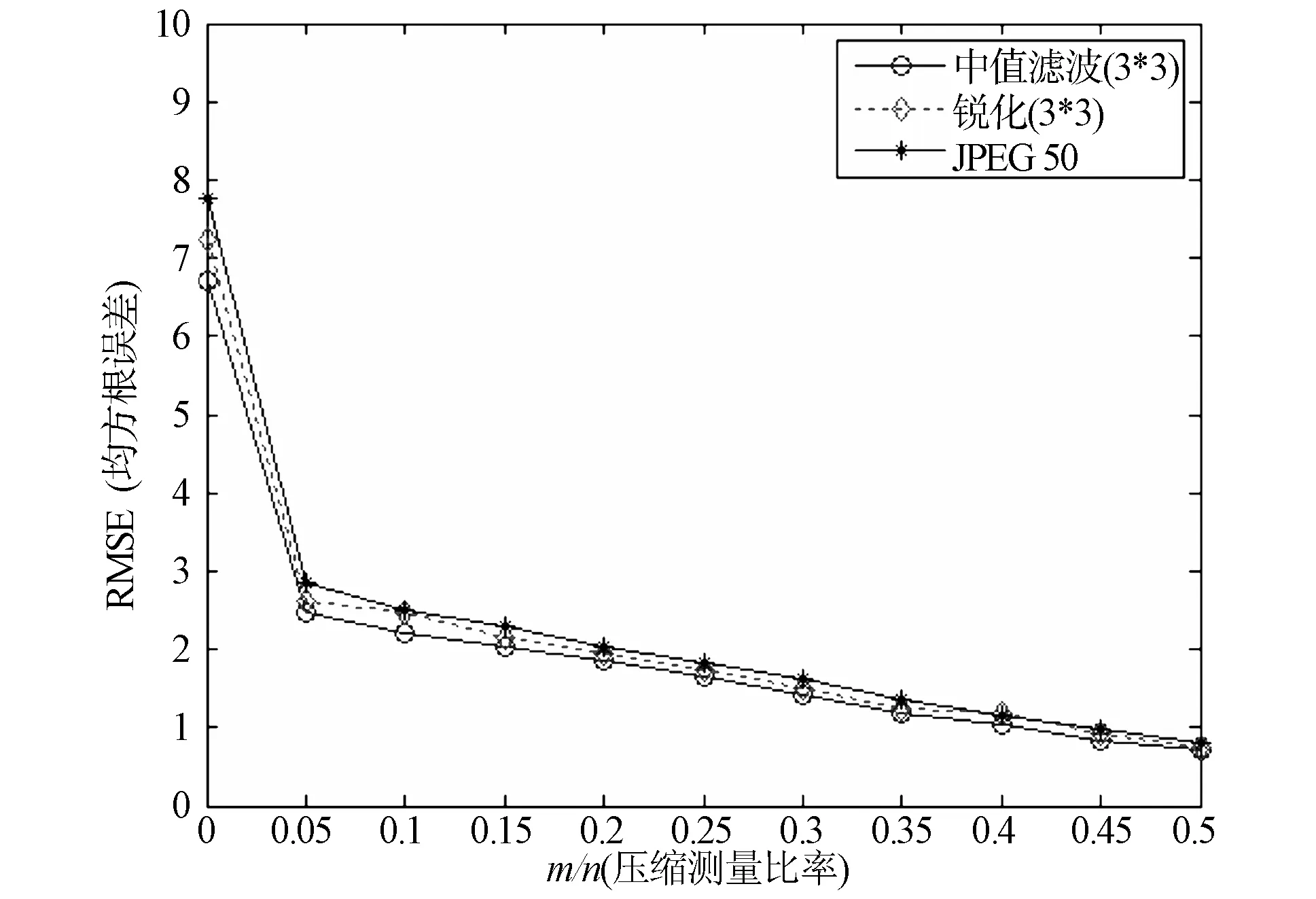
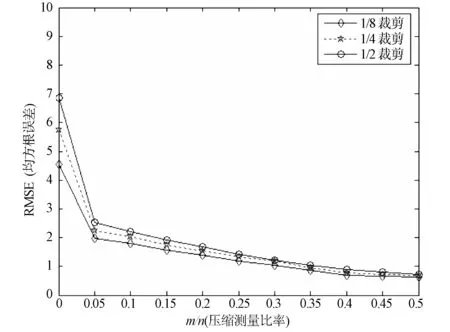
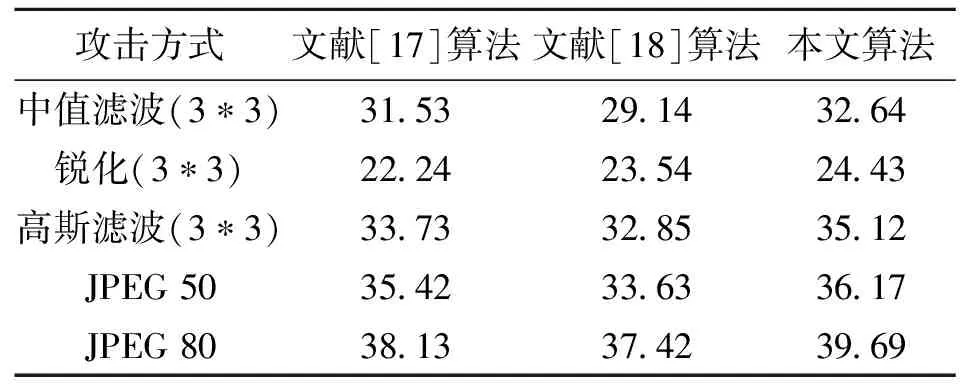
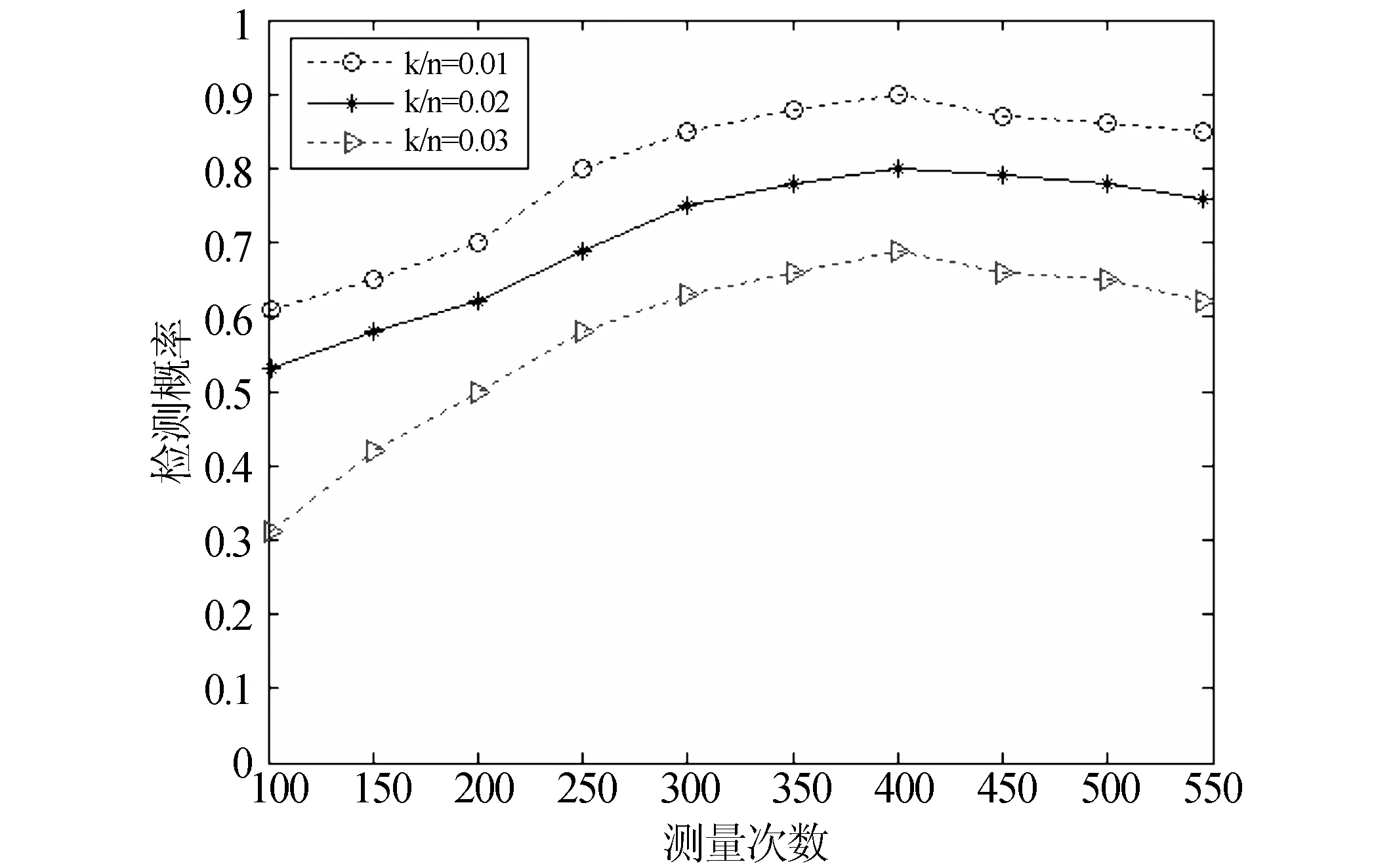
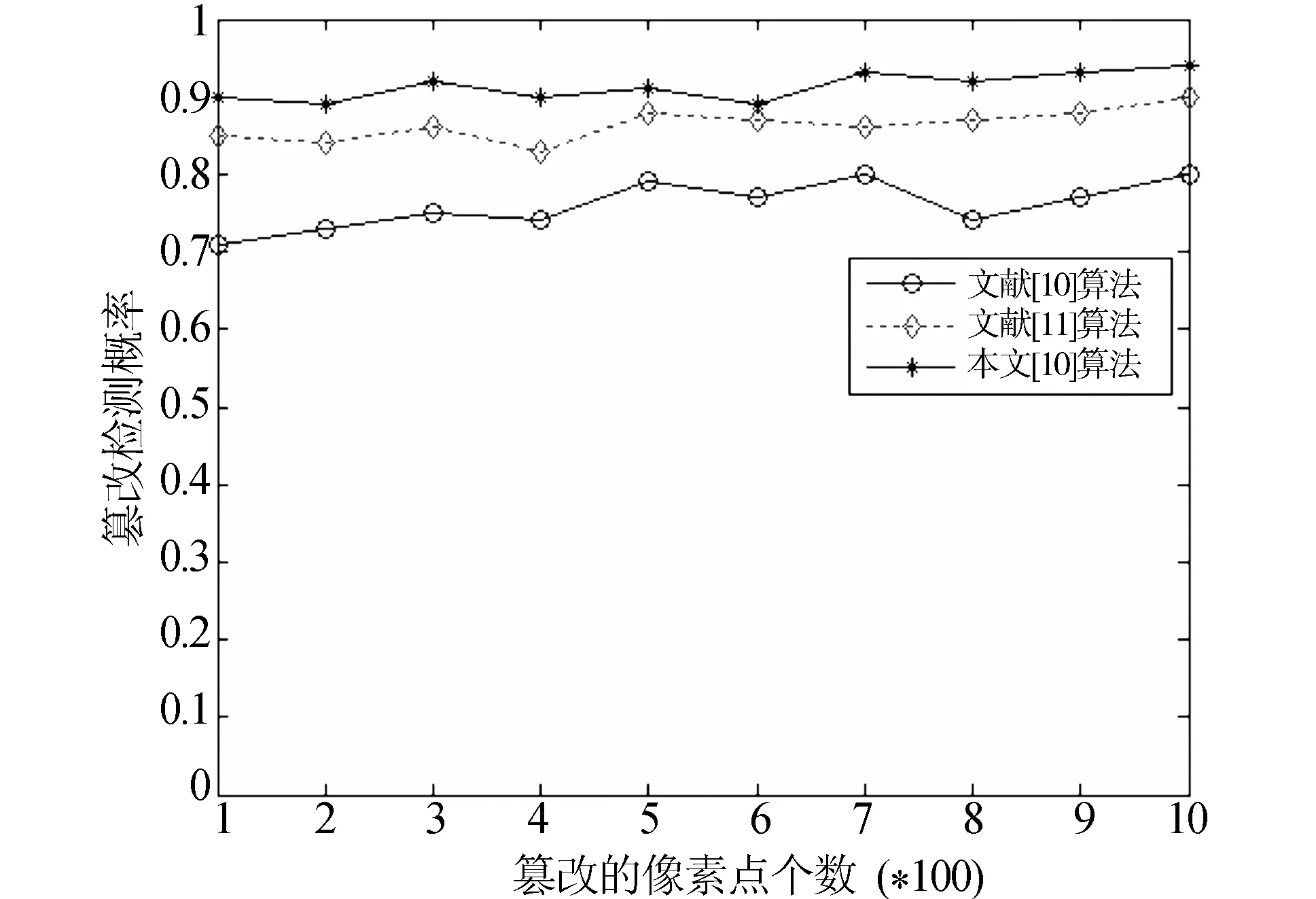
压缩传感(Compressive Sensing,CS)假定信号在某些基下能用少量非零系数表示。设x∈Rn代表一个自然信号,y∈Rm,m minimize ‖x‖0s.t.y=Ax (1) minimize ‖x‖1s.t.y=Ax (2) 这个问题可以转化为一个线性规划问题[10]。如果测量数目满足m≥C·klog2(n/k),那么问题(2)和(1)是等价的。如果x不是稀疏的,但在某些正交基下可以稀疏表示,则上述结果同样适用。本文主要利用压缩传感对原始图像和认证图像进行随机投影。 本文提出的基于压缩传感的图像哈希水印模型如图1所示。原始图像经过压缩传感随机投影,得到的压缩测量值作为图像内容特征,利用HMAC算法生成图像摘要,经过非对称加密,形成加密的水印信息,嵌入到原始图像的中低频系数上。 图1 基于压缩传感的图像哈希水印模型 压缩传感的关键是构建测量矩阵[11],测量矩阵是否合理影响着测量数据的多少。当测量矩阵为Fourier矩阵时[12],O(K*log(N))的投影测量数据量能将N维空间的K-稀疏信号精确重建。Fourier测量矩阵的构造算法如下: 设图像的大小N是素数,定义p0=1,pi是第i个素数,那么有 p0=1,p1=2,p2=3,p3=5,p4=7,… (3) 令q∈N,对于pq-1 k≤pq (4) 来构造一个测量矩阵 (5) 测量矩阵的行用rj,h表示,j∈[0,K)∩Ζ,h∈[0,pq+j)∩Ζ,对于每一行的第n列(n∈[0,N)∩Ζ),有 (6) 因此测量矩阵Φ可以表示为 (7) 利用上面公式可以得到如下的测量矩阵: (8) 由于对大尺度的整幅图像进行投影的计算量很大,并且非线性重构的代价较大,我们采用分块随机投影,其算法如下: 1)设原始图像X的大小N=Iτ×Ic,将图像分成大小为B×B的块,第i个图像块的向量形式记为xi,其中i=1...n,n=N/B2。 2)从测量矩阵Φ得到MB×B2的矩阵块ΦB,其中MB=(M×B2)/N|。 3)对xi采用相同的矩阵块ΦB进行投影测量,得到测量值向量: yi=ΦBxi (9) 4)对于整幅图像,测量矩阵Φ可以用如下的块对角矩阵表示: (10) 在该算法中,不需存储M×N的矩阵Φ,仅需存储MB×B2的矩阵块ΦB。显然,当B较小时需要的存储较小并能快速实现,而当B较大时能得到较好的重建效果,根据经验,取块的尺度B=32。 以压缩传感随机投影得到的压缩测量值作为哈希函数的输入,对输出的图像摘要进行非对称加密,得到加密的哈希水印。哈希函数采用带密钥的HMAC算法[13-14],该算法需要一个加密散列函数H(可以是MD5或者SHA-1)和一个密钥K。HMAC的计算公式如下: HMAC=H(KXOR opad,H(KXOR ipad,M)) (11) 其中,ipad是由B个字节0x36组成的字符串,opad是由B个字节0x5C组成的字符串。B表示数据块的字节数(MD5和SHA-1的分割数据块字长都是64),L表示散列函数的输出数据字节数(MD5中L=16,SHA-1中L=20)。密钥K的长度可以小于等于B,当大于B时,首先使用散列函数H对K进行转换,然后用H输出的L长度字符串作为在HMAC中实际使用的密钥。HMAC算法如下: 1) 在密钥K后面添加0来创建一个字长为B的字符串; 2) 将第1)步生成的B字长的字符串与ipad做异或运算; 3) 将随机投影得到的压缩测量值填充至第2)步的结果字符串中; 4) 用H作用于第3)步生成的数据流; 5) 将第1)步生成的B字长字符串与opad做异或运算; 6) 将第4)步的结果填充进第5)步的结果中; 7) 用H作用于第6)步生成的数据流,输出最终结果。 哈希水印的嵌入主要有两种方法[ 15-16],本文采用第二种方法[16]。将原始图像进行分块,将哈希水印嵌入到分块的中低频系数上,反转各分块系数,就完成水印的嵌入。 图像认证问题可以看作是假设检验问题,有如下两个假设: H0:图像不可认证 H1:图像可认证 从待认证图像中提取水印,经过非对称解密,得到原始图像的摘要,用h1表示。待认证图像同样采用分块随机投影,利用HMAC算法得到待认证图像的摘要,用h2表示。定义两者的汉明距离如下: (12) 其中,L是哈希的长度。如果: d(h1,h2)<η (13) 则认为图像是可认证的,η是一个确定性阀值。 为了验证本文算法的有效性,分别从水印鲁棒性以及篡改定位两方面对算法进行仿真实验和分析,实验环境为Windows XP、Matlab 7.0。 鲁棒性要求加入的水印能抵抗各种常规的信号处理,如平移、缩放、旋转、锐化、滤波等,以及一般性攻击,如裁剪。通过对加入水印的图像进行各种攻击,然后从受攻击图像中提取水印,并与原始水印进行对比来验证水印的鲁棒性。通常使用RMSE(均方根误差)和PSNR(峰值信噪比)来衡量水印的鲁棒性。RMSE的值越小,则水印的抗攻击能力越强。设n表示图像的大小(像素),m表示压缩传感随机测量数,m/n表示压缩测量比率。图2给出了Lena图像在几种常规信号处理下所对应的RMSE与压缩测量比率之间的关系,图3给出了Lena图像在不同的裁剪比例下所对应的RMSE与压缩测量比率之间的关系。当压缩测量比率较低时,极少量的压缩测量值无法完全表示图像的内容特征,当含水印图像受到攻击时,水印容易受到破坏,因此从受攻击图像中提取的水印与原始水印之间的RMSE值较大。当达到一定的压缩测量比率(这里是0.05)以后,RMSE变得很小,表明水印具有很强的鲁棒性。随着压缩测量比率的提高,RMSE变化不大,表明一定数量的压缩传感随机测量值就能够很好地表示图像的内容特征,由此生成的水印具有很强的鲁棒性。 图2 针对常规信号处理的水印鲁棒性分析 图3 针对剪裁几何攻击的水印鲁棒性分析 除RMSE以外,还可以利用PSNR来衡量水印的鲁棒性,PSNR定义如下: (14) WO是原始水印,WT是从受攻击图像中提取的水印。表1给出了文献[17]、文献[18]以及本文算法对不同的常规信号处理的水印鲁棒性能对比。从表中可以看出,本文的水印具有更强的鲁棒性。 表1 不同算法的水印鲁棒性比较 为了验证本文算法对图像篡改的定位能力,对含水印图像进行局部修改,例如:在图像中增加文本、景象,从图像中移除景象,然后采用本文算法进行篡改定位。图4是在图像中加入文本的篡改定位,图5是在图像中增加景象(插入青椒)的篡改定位,图6是在图像中移除景象(移除一棵小树)的篡改定位。从图中可以看出,本文算法具有较好的篡改检测和定位能力。 定义篡改检测概率为:P=Nd/Ne(Ne为随机篡改的像素点个数,Nd为实际检测到的像素点个数)。设n表示图像的大小(像素),k表示图像中非零系数的个数,k/n表示图像的稀疏度。图7给出了不同稀疏度的图像所对应的压缩传感测量数与篡改检测概率的关系。当测量次数较少时,其压缩测量值无法完全表示图像的内容特征,通过比较由压缩测量值表示的图像摘要来进行篡改检测和定位,其篡改检测概率相对较低。对于一幅512*512的图像,当测量次数为400时,篡改检测概率达到最高,随着测量次数的增加,篡改检测概率有所降低。在测量次数相同的条件下,图像的稀疏度越高(k/n的值越小),其篡改检测概率也越高。对Lena的含水印图像随机篡改若干个像素点,分别采用文献[17]、文献[18-19]以及本文算法进行篡改检测,图8给出了这几种算法的篡改检测概率对比。从图中可以看出,本文算法具有较高的篡改检测概率。 (a)原始图像 (b)篡改后的图像 (c)图像篡改定位结果 (a)原始图像 (b) 篡改后的图像 (c)图像篡改定位结果 (a)原始图像 (b) 篡改后的图像 (c)图像篡改定位结果 图7 测量次数与篡改检测概率的关系 图8 篡改检测概率对比 本文提出的基于压缩传感的图像哈希水印算法,通过压缩传感随机投影得到的压缩测量值可以作为图像的内容特征,由测量值生成的图像哈希水印具有很强的鲁棒性和安全性以及篡改检测能力,为新水印算法的研究提供了一个参考的途径。理论分析与实验结果表明,本文提出的算法与其他算法相比有着更高的检测概率、更强的鲁棒性以及更好的定位能力,因此有着更广阔的应用前景。 参考文献: [1] CANDES E J, WAKIN M B. An introduction to compressive sampling [J]. IEEE Signal Processing Magazine, 2008, 25(2): 21-30. [2] VALENZISE G, TAGLIASACCHI M, TUBARO S. A compressive-sensing based watermarking scheme for sparse image tampering identification[C]∥Image Processing (ICIP), 2009 16th IEEE International Conference, 2009: 1265-1268. [3] TAGLIASACCHI M, VALENZISE G, TUBARO S. Hash-based identification of sparse image tampering [J]. IEEE Transactions on Image Processing, 2009, 18(11): 2491-2504. [4] RICHARD B, MARK D, RONALD D. A simple proof of the restricted isometry property for random matrices [J]. Constructive Approximation, 2009, 3(28): 253-263. [5] CANDES E J. The restricted isometry property and its implications for compressed sensing [J]. Applied & Computational Mathematics, 2008, 346(1): 589-592. [6] WOJTASZCZYK P. Stability and instance optimality for Gaussian measurements in compressed sensing [J]. Foundations of Computational Mathematics, 2010, 10(1): 1-13. [7] ZHANG G S, JIAO S H, XU X L, WANG L. Compressed sensing and reconstruction with bernoulli matrices [C]. Information and Automation (ICIA), 2010 IEEE International Conference, 2010: 455-460. [8] CANDES E J, WAKIN M B. An introduction to compressive sampling [J]. IEEE Signal Processing Magazine, 2008, 25(2): 21-30. [9] WOJTASZCZYK P. Stability of l1 minimization in compressed sensing [C]∥Signal Processing with Adaptive Structured Representations (2009), 2009: 1-5. [10] SALIGRAMA V, ZHAO M Q. Thresholded basis pursuit: Quantizing linear programming solutions for optimal support recovery and approximation in compressed sensing[C]∥Preprint, 2008. [11] RACHLIN Y, BARON D. The secrecy of compressed sensing measurements [C]∥2008 46th Annual Allerton Conference, 2008: 813-817. [12] IWEN M. A deterministic sub-linear time sparse Fourier algorithm via non-adaptive compressed sensing methods [C]∥Proceedings of the Nineteenth Annual ACM-SIAM Symposium on Discrete Algorithms, 2008: 20-29. [13] 张宝华, 殷新春. RSA密码算法的安全及有效实现[J]. 中山大学学报: 自然科学版, 2008, 47(6): 22-26. [14] 韩国军, 刘星成. 基于校验节点的LDPC码的消息加权均值串行译码算法[J]. 中山大学学报: 自然科学版, 2010, 49 (3): 47-51. [15] 付炜, 邢广忠. 置换DCT域中频系数的盲水印嵌入算法研究[J]. 计算机应用研究, 2008, 24(3): 160-162. [16] 王员根, 梁凡, 肖明明. 一种彩色图像DC系数的自适应水印算法[J]. 中山大学学报: 自然科学版, 2010, 49 (4): 43-48. [17] TANG C W, HANG H M. A feature-based robust digital image watermarking scheme [J]. IEEE Transactions on Signal Processing, 2009, 51(4): 950-959. [18] LIN K Z, LI D Q, LI S H. Fragile image watermarking algorithm based on hash functions [J]. Journal of Harbin Engineering University, 2008, 29(1): 61-64. [19] 梁长垠, 李昂, 牛夏牧. 基于云水印的视频内容认证技术[J]. 中山大学学报: 自然科学版, 2009, 48(1): 26-30.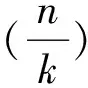
1.2 压缩传感的水印模型及算法分析
2 实验结果与分析



3 结 论
