空间散乱数据多项式自然样条光顺*
2010-06-05许伟志关履泰徐应祥
许伟志,关履泰,徐应祥
(中山大学科学计算与计算机应用系,广东 广州 510275)
多元散乱数据拟合广泛用于数据压缩、汽车外形设计、船体放样、飞机机翼机身设计、服装设计、地质探矿、医学图像处理等诸多领域,从上世纪60年代开始,众多研究工作者对散乱数据曲面拟合问题进行了一系列的研究[1-6]。但是都不如一元B样条处理一元散乱数据那样理想。李岳生和关履泰在1989年试图推广一元三次自然样条对散乱点插值的方法到二元情形,提出了散乱数据的二元多项式自然样条插值,研究了广义混合样条函数空间矩形域带连续边界条件和离散边界条件的多元散乱数据最优插值问题[7]。胡日章研究了相应的光顺逼近问题[8],韩国强从计算的角度提出了散乱数据光顺逼近二步法[9]。但是这类样条的目标泛函比较复杂,带有一系列的积分项[7- 8, 10],而且如果离散边界插值点不够多的话插值效果会比较差。为了克服这些缺点,关履泰、许伟志等研究了一类新的二元自然样条插值方法,该方法的目标泛函较为简单,没有离散边界插值点,更符合实际情况[11]。然而当测量数据受误差和噪声影响时,插值方法不如光顺方法那样能够很好地反映数据的本质。为此,本文在文[11]的基础上提出了一种多项式自然样条光顺方法,并研究了解的特征性质和解的结构。
1 问题的提出
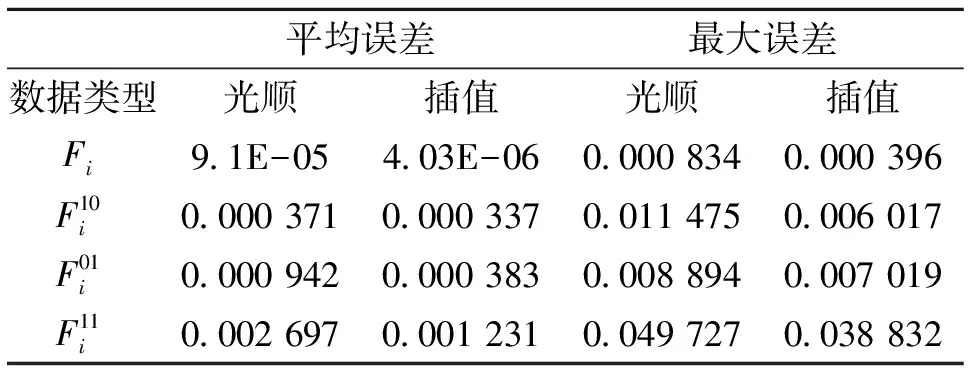
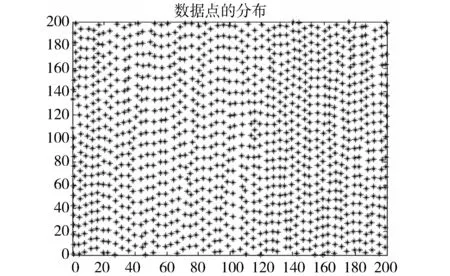
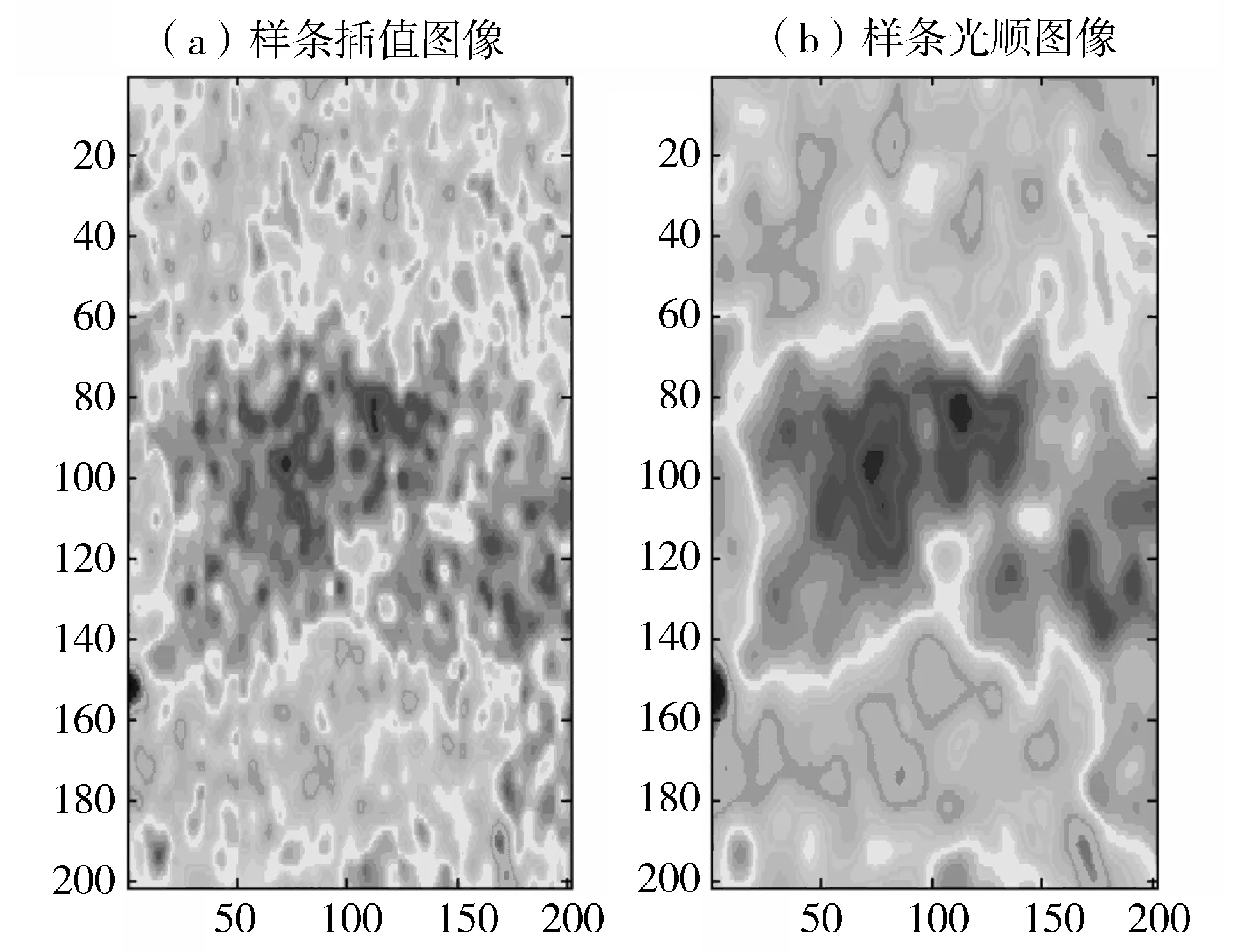
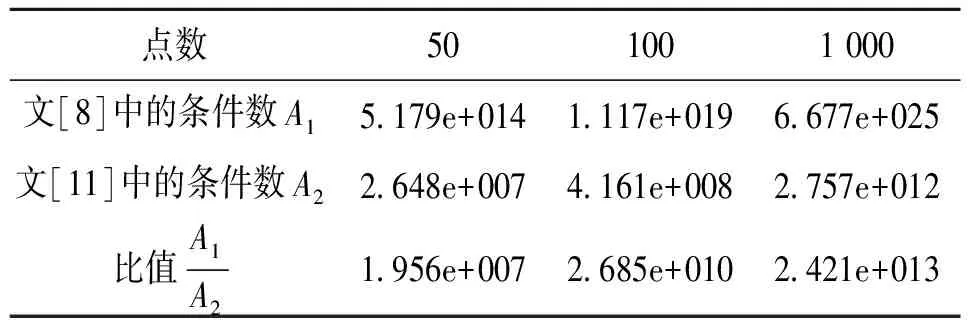
给定矩形区域R=[a1,a2]×[c1,c2],a Y=L2(R),T:X→Y是一个从X到Y的线性微分算子,在矩形区域R内定义为 在边界x=a,y=c上,它带边界条件 记Z=RN是N维欧几里得空间。假设A:X→Z是一个插值算子,定义为 Au=(u(x1,y1),…,u(xN,yN)) 为了方便,令z=(z1,…,zN)。考虑以下在希尔伯特空间Hm,n(R)中的样条光顺问题,称之为散乱点二元多项式自然样条光顺问题。 问题T寻找一个函数σ(x,y)∈X,满足 (1) 其中z=(z1,z2,…,zN),ρ>0是事先给定的常数。这里‖Tu‖2=∬R(u(m,n)(x,y))2dxdy,带边界条件 (2) 即寻找一个函数σ(x,y)∈X,满足 其中ρ>0,是事先给定的常数。带边界条件 容易验证下列引理。 引理1 算子T的化零子空间满足 N(T)=P〈m,n〉={u|u(x,y)= 定理1(特征定理)σ(x,y)∈X是二元多项式自然样条光顺问题解的充要条件为 ρ∬Rσ(m,n)(x,y)u(m,n)(x,y)dxdy+ (3) 对一切u(x,y)∈X成立。 证明(必要性) 设σ(x,y)∈X是二元多项式自然样条光顺问题的解,任意的u(x,y)∈X,ε为微小参数。记uε(x,y)=σ(x,y)+εu(x,y)代入问题(1)式,得 F(ε)=ρ∬R(σ(m,n)(x,y)+εu(m,n)(x,y))2dxdy+ 由于σ(x,y)∈X为问题T的解,所以F′(0)=0,即 F′(ε)=2ρ∬Ru(m,n)(x,y)· (σ(m,n)(x,y)+εu(m,n)(x,y))dxdy+ 即 ρ∬Rσ(m,n)(x,y)u(m,n)(x,y)dxdy+ J(u)=J(σ+u-σ)= J(σ)+J1(u-σ)+a(σ,u-σ) 由充分性条件,有 ρ∬Rσ(m,n)(x,y)u(m,n)(x,y)dxdy+ 对一切u(x,y)∈X都成立。那么对于u-σ∈X, 有 ρ∬Rσ(m,n)(x,y)(u(m,n)(x,y)-σ(m,n)(x,y))dxdy+ 引理2 设σ(x,y)∈X是二元多项式自然样条光顺的解,那么必存在系数λi与ki(i=1,…,N)使得 证明由特征定理可知 ρ∬Rσ(m,n)(x,y)u(m,n)(x,y)dxdy+ 即 Au(x,y)=(u(x1,y1),…,u(xN,yN))= ((k1,u),…,(kN,u)) 定理2 二元多项式自然样条光顺函数σ(x,y)具有如下的显式及紧凑格式的表达式 其中gi(x,y)=G(xi,m,a;x)G(yi,n,c;y),i=1,…,N是(2m-1,2n-1)次自然样条基函数,并且有 对任意X中的元素u,在a点Taylor展开 u(x,y)=u(a,y)+(x-a)u(1,0)(a,y)+…+ 然后在c点Taylor展开u(a,y),u(1,0)(a,y),…,u(m-1,0)(a,y),u(m,0)(τ,y)得 u(xi,yi)=u(a,c)+(yi-c)u(0,1)(a,c)+…+ (xi-a)u(1,0)(a,c)+…+ 利用上面结论,并注意边界条件,对任意X中的元素u有 f(x,y)∈N(T) 其中gi(x,y)=G(xi,m,a;x)G(yi,n,c;y),i=1,…,N。满足 所以 其中gi(x,y)=G(xi,m,a;x)G(yi,n,c;y),i=1,…,N是(2m-1,2n-1)次自然样条基函数,并且有 且 v=0,…,n-1 从求n-1阶导数开始,由上式推出 然后,利用这个结果代入求n-2阶导数的式子中得到 (n-2)!cn-2(yi,n,c;y)+ cn-2(yi,n,c;y)= 再用上述这些结果,代入求n-3阶导数的式子中,有 (n-3)!cn-3(yi,n,c;y)+ (n-3)!(cn-2(yi,n,c;y)(y-c)+ cn-3(yi,n,c;y)= 继续下去……,得到 定理3 如果相应的齐次多项式光顺问题只有恒零解,则对任意散乱数据(xi,yi,zi),i=1,…,N,(2m-1,2n-1)次多项式自然样条光顺问题有唯一解,可表示为 其中gi(x,y)=G(xi,m,a;x)G(yi,n,c;y),i=1,…,N是(2m-1,2n-1)次自然样条基函数,并且有 且 cij及λi由以下的方程组来确定 其中 Λ=(λ1,…,λN)T,z=(z1,…,zN)T, C=(c00,c01,c02,…,c0(n-1), c10,c11,…,c1(n-1),…,c(m-1)(n-1))T, A=(aij)N×N, 证明由特征定理可知,σ(x,y)∈X是二元多项式自然样条光顺问题解的充要条件为 ρ∬Rσ(m,n)(x,y)u(m,n)(x,y)dxdy+ (5) 对一切u(x,y)∈X成立。又由引理2知 代入(5)式得 即 再由u(x,y)的任意性可知ρλi+σ(xi,yi)-zi=0,i=1,2,…,N。即 得到前N个方程。注意在定理2的证明过程中,我们已经得出 这就是后面m×n个方程。写成矩阵形式后则证得本定理。由二项式定理可证以下结论。 由定理3和定理4可得求光顺函数算法如下: (ⅰ)输入散乱数据点(xi,yi),i=1,…,N与要在其上拟合的数据zi,i=1,…,N及合适的光顺参数ρ; (ⅱ)计算矩阵A; (ⅴ)求出光顺函数 例1 拟合函数:z=1/(1+x2+y2),区间:[0,1]×[0,1],边界:a=-1,c=-1。对301个散乱点(由随机数产生)相应的函数值,分别运用双三次自然样条光顺方法(ρ=0.005)与双三次自然样条插值方法去拟合函数, 比较它们在所在区域30×30个格子点上的函数值Fi,导函数值的平均误差与最大误差(见表1)。 表1 301个散乱数据插值和光顺的函数值、导函数值误差 一般地,选取合适参数的光顺样条方法得出的曲面较用插值方法得到的曲面光滑。 例2 某地区重金属钍的3 580个测量值[6],分布如图1,分别用双三次自然样条插值和光顺(ρ=0.012),应用极小残量法(Generalized Minimal Residual Algorithm)迭代求解对称不定的线性方程组[12],得到的结果(如图2)。 图1 数据点的分布 图2 (a)插值图像 (b)光顺图像(ρ=0.012) 由于测量数据存在误差和噪声,插值图像并不能很好的反映重金属钍的分布情况,而光顺图像很好地反映了重金属钍的实际分布情况。 例3 拟合函数:z=cos(x)×sin(y)区间:[0,4]×[0,4],对50、100、1 000个散乱点(由随机数产生)相应的函数值,分别用文[11]和文[8]中的双三次自然样条插值方法去拟合函数,相应的系数矩阵的条件数比较如表2。 表2 方法[8]和[11]中的系数矩阵条件数比较 对相同散乱数据进行双三次样条插值拟合,本文中方程组的系数矩阵条件数比文[8]中的系数矩阵条件数小,更适合大规模散乱数据拟合。 结论:选取合适参数的光顺样条方法得出的曲面较平滑,外形比用插值方法好。在实际应用中,当数据有误差和噪声时,建议选取适当参数应用光顺样条方法获得拟合曲面。另外,本文的方法容易推广到高维情形。本文中方程组的系数矩阵条件数比文[8]中的系数矩阵条件数小,更适合大规模散乱数据拟合。 参考文献: [1] WAHBA G. Spline models for observational data[J]. Soc Ind Appl Math, 1990. [2] GUAN L T, LIU B. Surface design by natural splines over refined grid points[J]. J Comp Anal and Appl, 2004, 163(1):107-115. [3] LAI M J. Multivariate splines for data fitting and approximation, Approximation Theory XII[M]. San Antonio, 2007, edited by Neamtu M and Schumaker L L, Brentwood :Nashboro Press, 2008: 210-228. [4] LAI M J, SCHUMAKER L L. Spline functions over triangulations[M]. London: Cambridge University Press, 2007. [5] 吴宗敏. 散乱数据拟合的模型、方法和理论[M]. 北京:科学出版社, 2008. [6] BILLINGS S D, NEWSAM G N, BEATSON R K. Smooth fitting of geophysical data using continuous global surfaces[J]. Geophysics, 2002, 67 (6): 1810-1822. [7] 李岳生, 胡日章. 多元散乱数据的样条插值法[J]. 高等学校计算数学学报, 1990, 3: 215-226. [8] 胡日章. 矩形域上散乱数据的离散边界条件光顺逼近[J]. 中山大学学报:自然科学版, 1990, 29(4): 17-22. [9] 韩国强. 矩形域上散乱数据样条光顺法[J]. 华南理工大学学报:自然科学版, 1993, 21(4): 102-109. [10] GUAN L T. Bivariate polynomial natural spline interpolation algorithms with local basis for scattered data[J]. J Comp Anal and Appl, 2003, 1: 77-101. [11] 关履泰,许伟志,朱庆勇. 一种散乱点双三次多项式自然样条插值[J]. 中山大学学报:自然科学版, 2008, 47(5): 1-4. [12] SAAD Y, SCHULTZ M H. GMRES: A generalized minimal residual algorithm for solving nonsymmetric linear systems[J]. SIAM J Sci Stat Comput, 1986, 7(3): 856-869.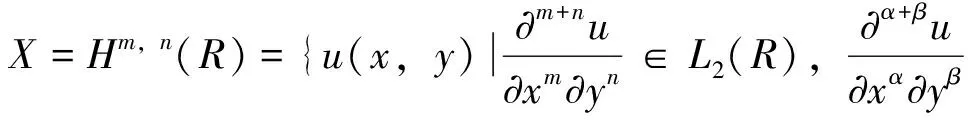
2 带边界条件的自然样条基函数的构造
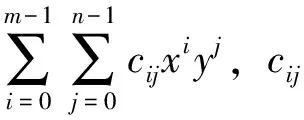
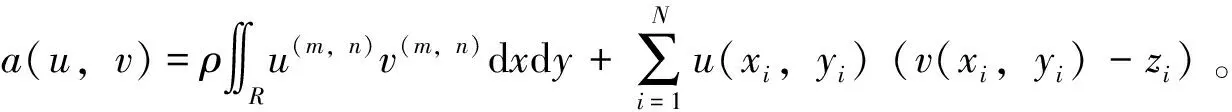
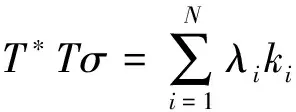
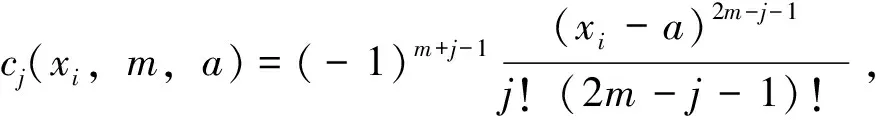
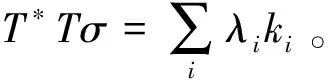
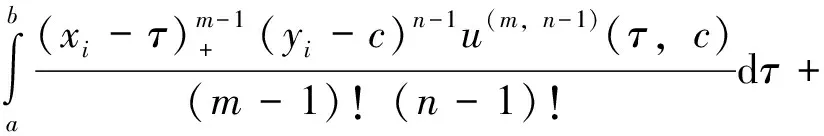
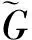
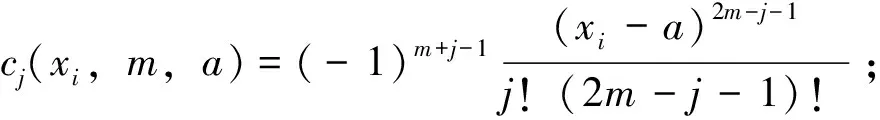
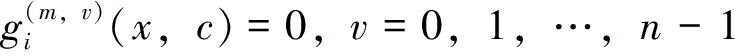
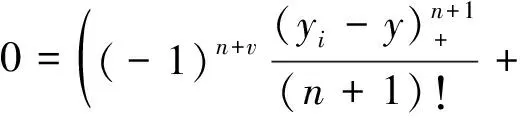
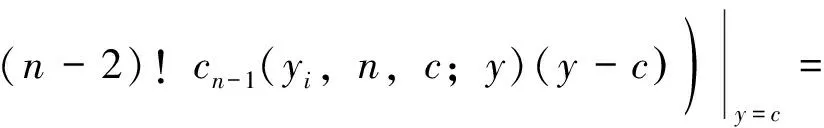
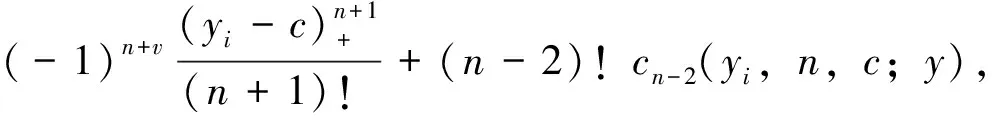
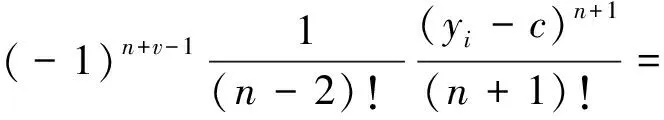
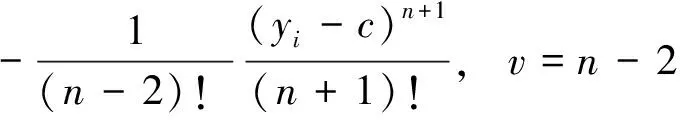
3 散乱点自然样条光顺问题求解
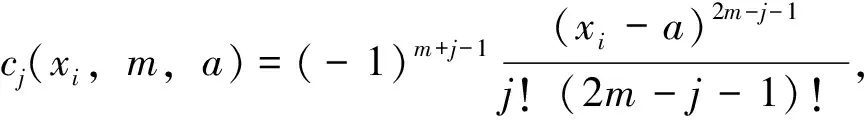
4 求光顺函数算法
5 算 例