两端边值问题的通用精细积分法*
2010-06-05张文志富明慧蓝林华
张文志,富明慧,蓝林华
(中山大学应用力学与工程系∥广东省近岸海洋工程重点实验室,广东 广州 510275)
钟万勰[1-2]提出的精细积分法由于具有高精度、高效率、稳定性好等诸多优点,在各类数学物理方程的求解中获得了日益广泛的应用。然而,现有的精细积分法的研究工作,绝大多数都针对于初值问题,相比之下,有关边值问题的研究极少[3-8]。对于常微分方程的边值问题,一种自然的想法是将其转化为初值问题来处理,如打靶法,但当模拟时间轴长度较大时,该方法可能会导致求解问题的病态[9]。为了克服这一问题,钟万勰[10-12]研究了齐次微分方程组的边值问题,建立了一种可以避免病态的精细积分方法(称为黎卡提方法)。Chen等利用“增维”的思想将非齐次方程化为齐次方程,从而使黎卡提方法对非齐次方程也能适用[13]。
本文在上述工作基础上,将边值问题精细积分法做了进一步推广。首先利用传递矩阵建立区段代数方程,并由此导出区段合并消元的递推公式,这个环节由于能直接利用传递矩阵的计算结果,从而避免了不必要的计算,在很大程度上提高了计算效率;另外本文提出的方法比黎卡提方法更容易处理复杂边界条件,从而拓宽了适用范围。
1 两点边值问题的精细积分
考虑如下边值问题
(1)
(2)
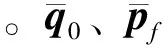
方程(1)的解可表达为
(3)
将区间[0,xf]均匀划分为m(m=2M)份,则步长τ=xf/m。记xi=iτ,qi=q(xi),由方程(3)可得
(4)
其中,T=exp(Hτ)是传递矩阵,其精细算法可见文献[1-2]。
如果求出p0,则由式(4)便可计算出所有结点上q、p的值。由式(4),可得
(5)
上式中未知量为qf、p0。未知量个数为2n,方程总数也是2n,故可求解。但当区间长度较大时,按上式求解可能会导致病态问题。为此,钟万勰提出了一种可避免病态问题的区段合并消元方法[10-12]。本文则从另外一个角度出发,提出了一种更为有效的区段合并消元方法。
首先考虑第一个区段(0,x1)上起点终点的状态参量间的关系,在式(4)中取i=0,并将T采用分块记法,有
(6)
其中,T11、T12、T21、T22为n阶矩阵。将q0、p1视为已知,求解上述方程可得
(7)
其中
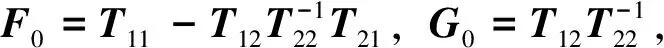
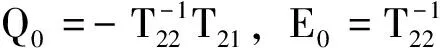
(8)
由于τ是很短的区间,故上述求解过程不会引起病态问题。同理可以给出
(9)
下面将(0,x2)作为一个区段,考虑其起点终点状态参量间的关系,视q0、p2为已知,并消去q1、p1,有
(10)
其中
(11)
以此类推,可以得到如下递推关系
(12)
其中
(13)
在式(12)中经过M次递推运算,就可以确定出q0、pf
(14)
求出p0以后,可由式(4)确定出任意内部节点的状态参量。
上述区段消元的递推过程与文献[10-12]有相似之处,但也存在着明显的区别。那就是消元过程不是“从头”做起,而是在传递矩阵的基础上进行,因而效率更高。更重要的一点是,本文方法可以处理更一般的边界条件。
2 另一种边界条件的情况
设方程(1)满足的边界条件为
(15)
由式(6)可得
(16)
其中
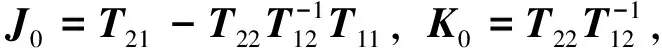
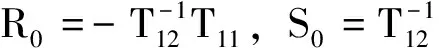
(17)
类似于上节区段合并消元方法,可得如下递推关系
(18)
其中
(19)
这样,由式(18)经过M次递推可得到
(20)
完全类似地,可以得到两端边界条件均为p的结果。实际上将式(16)中的q、p互换并将式(17)中的下标1和2互换即可。
3 边界条件更为普遍的情况
设x=0时的边界条件为
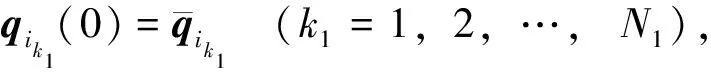
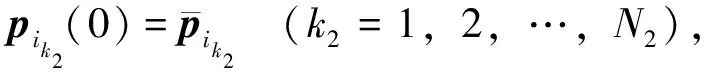
(N1+N2=n)
(21)
x=xf时的边界条件为
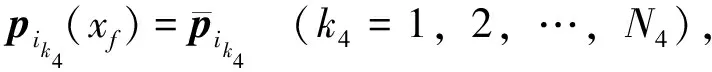
(N3+N4=n)
(22)
引入初等变换矩阵P、Q,初等变换矩阵的作用是使矩阵或向量换行或换列[14]。定义
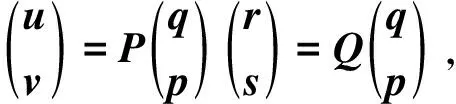
(23)
其中,u、v、r、s均为n维向量,A、D、B、C为n阶矩阵。P、Q均为2n阶的初等矩阵。通过适当的选择P、Q,可以使得在x=0时u为已知,v为未知,在x=xf时r为未知,s为已知。由上式及式(4)可得
(24)
考虑第一个区段(0,x1)上起点终点的状态参量间的关系,在式(24)中取i=0,并将QTP-1采用分块记法,有
(25)
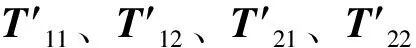
(26)
其中
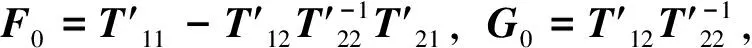
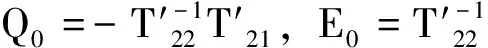
(27)
同理,有
(28)
考虑区段(0,x2)的起点终点状态参量间的关系,视u0、s2为已知,并消去r1、v1及u1、s1,有
(29)
其中
(30)
以此类推,可得如下递推关系
(31)
其中
(32)
由(31),经过M次运算,就可以确定出v0、rf
(33)
求出v0以后,可由式(24)确定出任意内部节点的状态参量。
4 非齐次方程的情况
对于非齐次方程问题,当非齐次项符合增维条件时,可先按文献[13]的方法,将其转化为齐次方程,然后用本文所述方法计算。
下面考虑非齐次项更一般的情况。设非齐次方程为
(34)
q(0)=q0,p(xf)=pf
(35)
其中,q、p是n维未知向量,H是2n阶系数矩阵。q0、pf是n维已知向量。式(34)的解为
(36)
其中,上标“0”表示齐次方程的通解,上标“*”表示非齐次方程的一个特解。
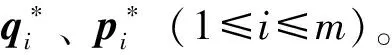
(37)
按照第一节介绍的方法,求出满足边界条件(37)的齐次方程的解后,再与非齐次方程特解叠加,便可得到问题的最后解答。
5 算 例
例1 考虑一个二维刚度问题(见文献[9], p.739)
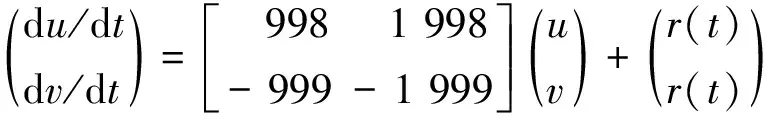
这里以r(t)=exp(-t)为例,其精确解为
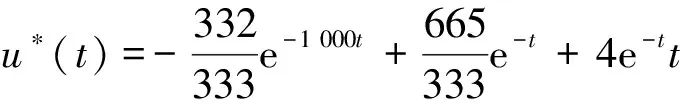
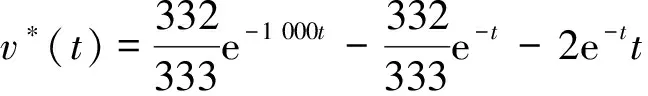
和文献[13]的做法一样,由该精确解确定的u|t=0和v|t=1作为两端边界条件。本文按照式(36)、(37)的方式进行计算。其中非齐次方程的特解由广义精细积分给出[8]。取M=0,本文的计算结果与文献[13]黎卡提方法所得结果的对比见表1。
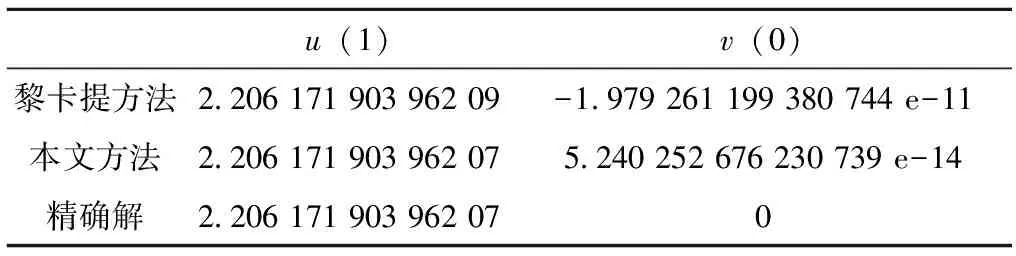
表1 本文结果与黎卡提法结果的对比
值得注意的是,文献[13]给出的解答仅小数点后10位数字,我们重新计算补充了后面的数字。由表1可以看出,与黎卡提方法的结果相比,本文结果精度更高,已可视为计算机上的“精确解”。
例2 考虑如下的两个自由度的无阻尼结构动力方程:
(38)
其中
已知方程(38)的一个精确解为
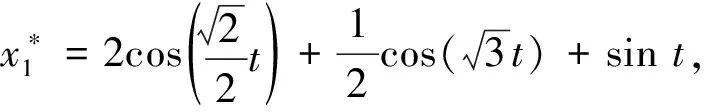
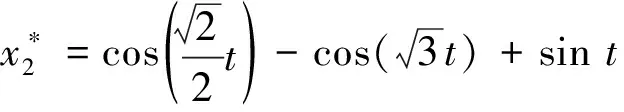
下面利用此精确解研究本文方法的精度。
首先考虑tf=10的情况。假设方程(38)的两端边界条件为:
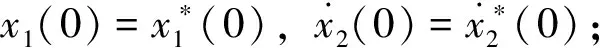
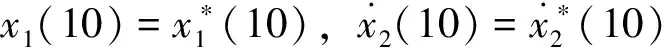
这种边界条件是文献[13]的方法所不易求解的。本文计算时先利用增维精细积分将非齐次方程化为齐次方程,然后按本文第三节的方法取M=0进行计算,计算结果如表2。由表2可以看出,本文结果的精度可达到14位有效数字。
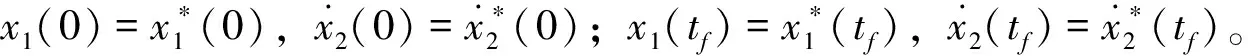
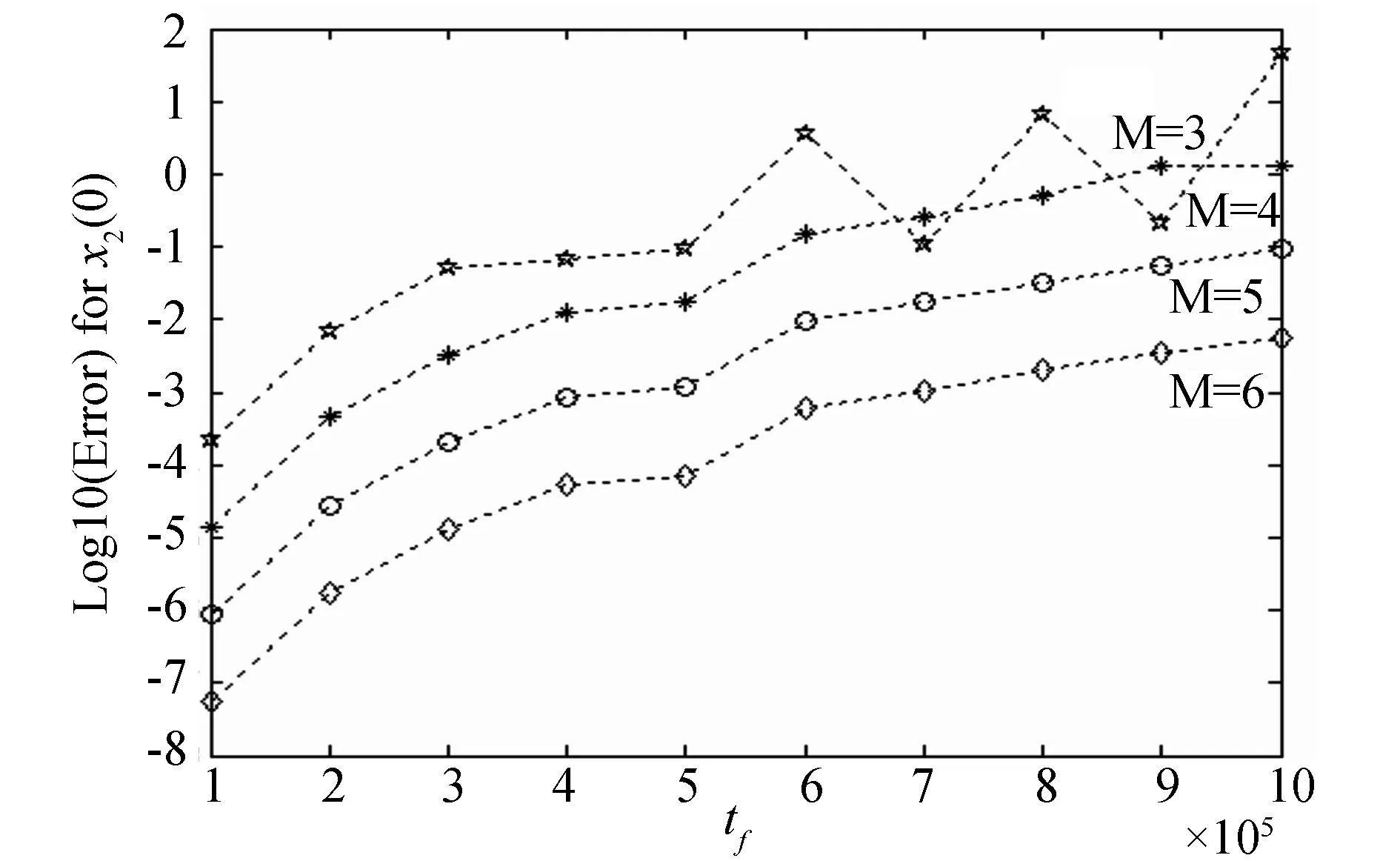
图1 x2(0)的Log10(Error)-tf曲线
由图1可以看出,当M固定时,区间长度越大,结果误差越大;而当区间长度固定时,M越大时误差越小。故当长度很大时,计算时应适当增大M值,以保证解答具有足够的精度。

表2 本文结果与精确解的对比
6 结 论
本文提出了求解常微分方程组两点边值问题的一种通用精细积分解法。该方法比原有黎卡提方法能更容易处理复杂边界条件,且效率也有一定的提高。
参考文献:
[1] 钟万勰. 结构动力方程的精细时程积分[J]. 大连理工大学学报, 1994, 34(2): 131-135.
[2] ZHONG W X, WILLIAMS F W. A precise time step integration method[J]. Journal of Mechanical Engineering Science, 1994, 209: 427-436.
[3] ZHONG W X, ZHU J N, ZHONG X X. On a new time integration method for solving time dependent partial differential equations[J]. Comput Methods Appl Mech Engrg, 1996, 130: 163-178.
[4] ZHANG H W, CHEN B S, GU Y X. An adaptive algorithm of precise integration for transient analysis[J]. Acta Mechanica Solida Sinica, 2001, 14(3): 215-224.
[5] GU Y X, CHEN B S, ZHANG H W, et al. Precise time integration method with dimensional expanding for structural dynamic equations[J]. AIAA Journal, 2001, 39(12): 2394-2399.
[6] 谭述君,钟万勰. 非齐次动力方程Duhamel项的精细积分[J]. 力学学报, 2007, 39(3): 374-381.
[7] 富明慧,梁华力.一种改进的精细-龙格库塔法[J].中山大学学报:自然科学版, 2009, 48 (5):1-5.
[8] 富明慧, 刘祚秋, 林敬华. 一种广义精细积分法[J]. 力学学报, 2007, 39(5): 672-677.
[9] PRESS W H, TEUKOLSKY S A, VETTERLING W, et al. Numerical recipes in C++: The Art of Scientific Computing[M]. 2nd. Cambridge University Press, Cambridge, 2002.
[10] 钟万勰. 弹性力学求解新体系[M]. 大连:大连理工大学出版社,1995.
[11] ZHONG W X. Combined method for the solution of asymmetric riccati differential equations[J]. Computer Methods in Applied Mechanics and Engineering, 2001, 191: 93-102.
[12] 钟万勰. 应用力学对偶体系[M]. 北京:科学出版社, 2002.
[13] CHEN B S, TONG L Y, GU Y X. Precise time integration for linear two-point boundary value problems[J]. Appl Math Comput, 2006, 175: 182-211.
[14] 同济大学数学教研室. 工程数学:线性代数[M].3版.北京:高等教育出版社,1999.
