智能车辆自适应巡航控制系统建模与仿真

李以农 冀 杰 郑 玲 赵树恩

重庆大学机械传动国家重点实验室,重庆,400044

0 引言

自适应巡航控制系统是为提高车辆纵向运动主动安全性而设计的自动辅助驾驶系统,是实现车辆自动化和智能化的一个重要组成部分[1-2]。它能够根据车辆行驶及道路环境的变化,实时控制智能车辆与其他车辆之间的相对间距和相对速度,从而有效减轻驾驶员在驾驶过程中的操作负担,增大道路的交通流量,提高车辆行驶的主动安全性[3]。

智能车辆自适应巡航控制系统所处的行驶工况复杂,且存在较强的非线性和不确定性因素,因此,国内外学者对车辆动力传动系统建模及控制系统设计进行了相关研究。文献[4]建立了车辆动力传动系统的经验模型,并利用最小二乘法对未知的车辆参数进行了估计;文献[5-7]利用模糊逻辑理论对车辆的相对速度和间距进行控制,有效提高了控制系统的跟踪性和鲁棒性;文献[8-9]在复杂多变的城市交通环境下,对自适应巡航控制系统的走-停功能及耦合效应进行了深入研究,提高了车辆在低速、拥挤交通工况下的主动安全性。以上文献在自适应巡航控制系统的研究过程中,对动力传动系统的各机构进行了不同程度的简化,没有全面考虑动力传动系统的非线性特性及轮胎模型的滑移特性对车辆纵向动力学特性的影响,因此,很难反映自适应巡航控制系统在换挡、制动等行驶工况下的控制效果。

基于以上分析,本文首先建立了相对完整的动力传动系统模型,获得了该模型的稳态逆向动力学特性曲线;然后基于模糊逻辑和滑模控制理论设计自适应巡航控制系统,使被控车辆能够准确跟踪期望加速度;最后,利用计算机仿真技术验证了自适应巡航控制系统在加速行驶、车辆跟踪和制动减速等复杂行驶工况下的跟踪性和适应性。

1 车辆动力传动系统数学模型

某车型的动力传动系统布置采用发动机前置、后轮驱动的形式,动力传动系统模型的输入信号为发动机的节气门开度或制动力矩,输出信号为车辆的行驶速度,该车型动力传动系统的组成及传递方向如图1所示。

1.1 发动机模型

忽略节气门滞后时间及驱动轴扭转刚度对发动机性能的影响,获得发动机稳态输出转矩T e与发动机转速n e和节气门开度α之间的函数关系：

图1 车辆动力传动系统结构框图

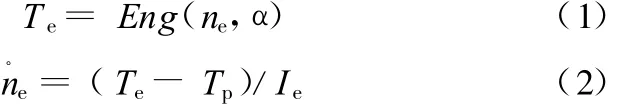
式中,Eng(◦)为发动机转矩的特性函数;Tp为液力变矩器泵轮的输入转矩;Ie为发动机的转动惯量。

发动机关于节气门开度和转速的稳态输出转矩特性如图2所示。

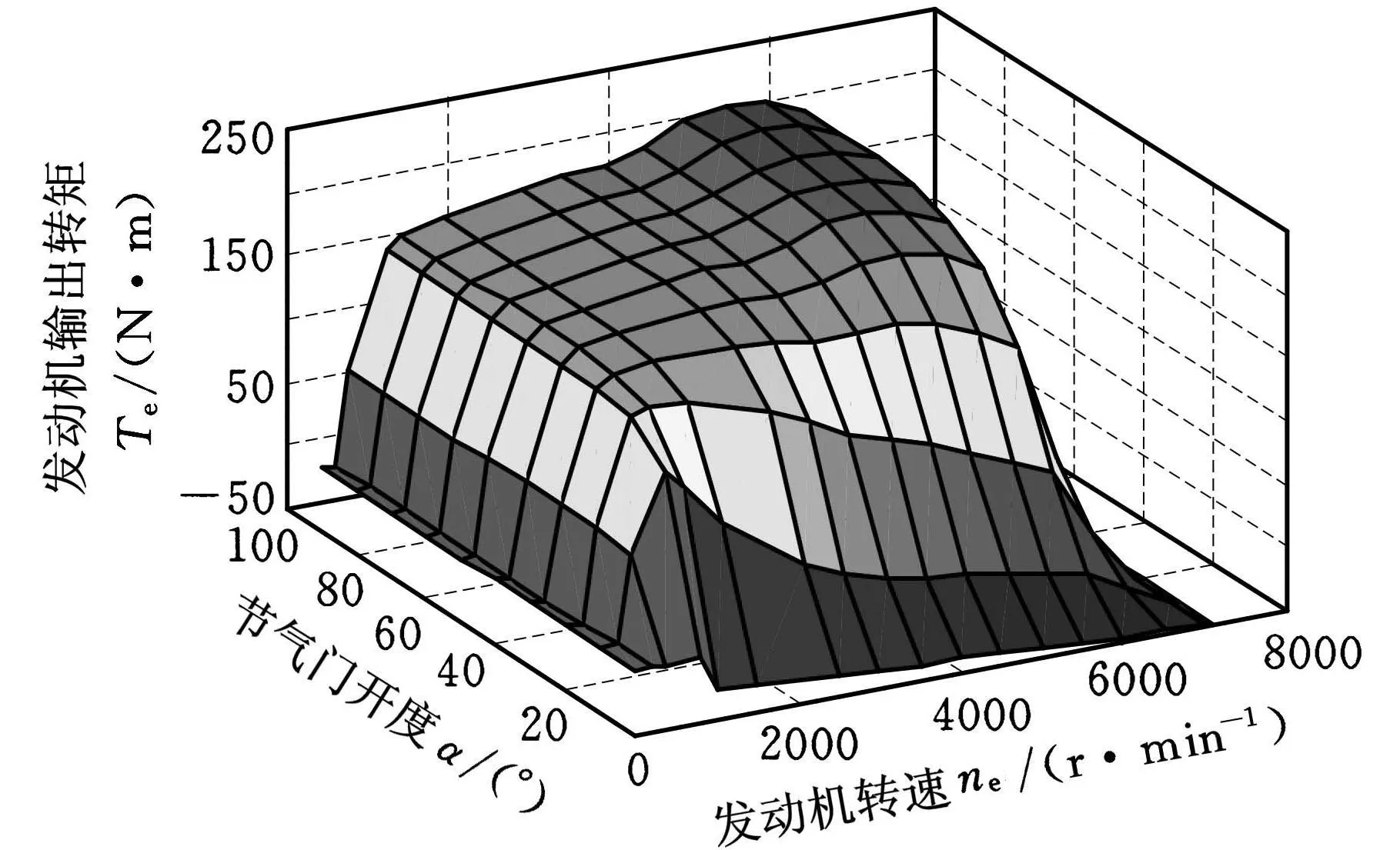
图2 发动机稳态输出转矩

1.2 液力变矩器模型

液力变矩器输入转矩T p的大小取决于泵轮的转速np和变矩器的容量特性系数Cp(rn),即

容量特性系数是以变矩器输出转速nt与输入转速np的比率r n为变量的函数,容量特性系数曲线如图3所示。

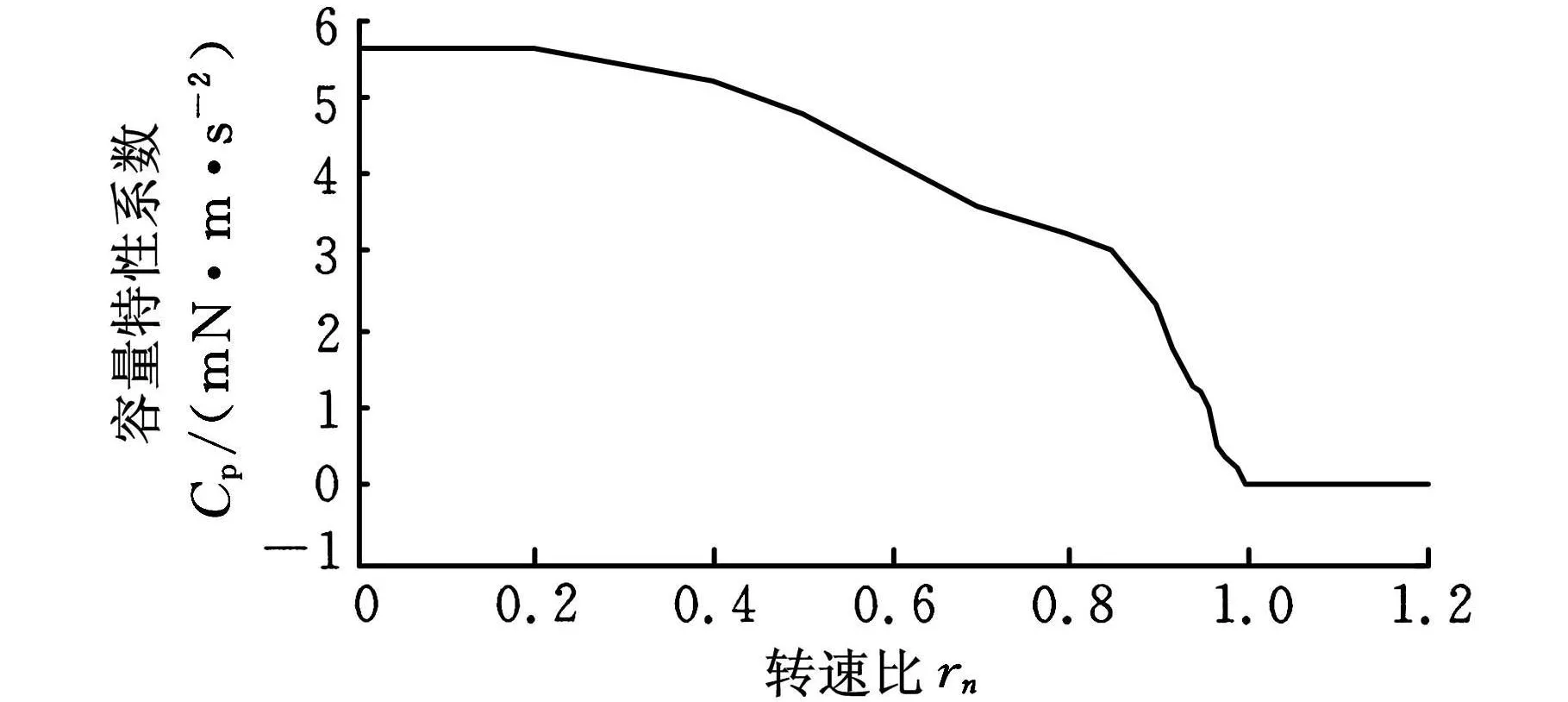
图3 液力变矩器容量特性曲线

液力变矩器的涡轮输出转矩 T t与泵轮输入转矩Tp之间的比值称为转矩特性,它与液力变矩器转速比r n之间的关系曲线如图4所示,利用转矩特性系数K p(rn)可得出变矩器输出转矩T t：

1.3 自动变速器

图4 液力变矩器转矩特性曲线

该车型采用四挡自动变速器,4个挡位的变速比 分别为 3.571 、2.200、1.500 、1.000,在 仿真实验研究中,利用有限状态机理论描述自动变速器的挡位切换行为[10],并利用MATLAB软件中的Stateflow模块建立挡位切换模型。自动变速器的挡位切换规则与节气门开度α和自动变速器输出转速nt相关,不同行驶状态下的升挡及降挡曲线如图5所示。

图5 自动变速器挡位切换规则

液力变矩器涡轮的输出转矩Tt和转速nt经过自动变速器和主减速器传递到驱动轮,可得到驱动轴转矩T w和驱动轮转速ωwr：

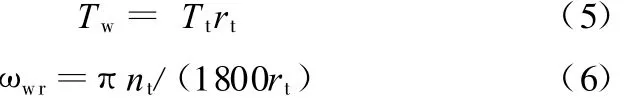
式中,rt为动力传动系统的总传动比,rt=rgr0;rg为自动变速器传动比;r0为主减速器传动比。

1.4 非线性轮胎模型

采用文献[11]提出的TMeasy轮胎模型描述轮胎纵向力的非线性特性,定义轮胎的纵向滑移率sxi为

式中,sxi(i=f,r)分别表示前后车轮的纵向滑移率;vx为车辆的行驶速度;Rw为轮胎的有效半径;vco为速度常数;ωw为车轮的角速度。

在TMeasy轮胎模型的稳态工况下,轮胎的纵向滑移率与纵向力之间的关系由轮胎最大纵向作用力F m、F m对应的纵向滑移率s m、曲线斜率趋于恒定时的轮胎纵向作用力F g、F g对应的纵向滑移率s g、F g对应的曲线斜率K g、轮胎纵向力曲线在原点处的斜率K06个特性参数决定,对以上参数进行分段多项式拟合,可得到轮胎纵向力F xi的分段函数表达式：

当 0 ≤sxi≤sm时,σt=sxi/sm,有

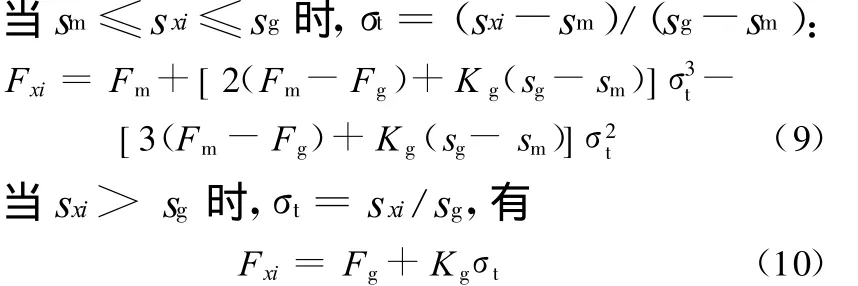
其中,变量σt为分段函数的差值变量。不同载荷F L下的轮胎纵向力非线性特性曲线如图6所示。

图6 轮胎纵向力非线性特性曲线

1.5 制动器模型

前后制动系统均采用盘式制动器,添加响应滞后时间t b来描述制动过程中的时滞现象,制动器的数学模型为

式中,Tb为车辆的制动力矩;μbr为制动器摩擦因数;Abr为制动盘摩擦面积;Rbr为制动力作用半径;pbr为制动器压力。

1.6 车辆纵向运动动力学

假设各车轮转动惯量I w相等,有效半径R w相等,滚动阻力因数 f0不变,得到前后车轮的运动方程分别为

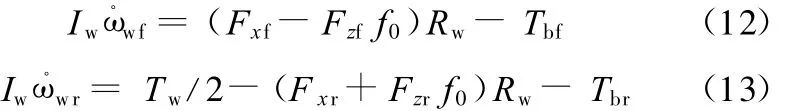
其中 ,ωwf、ωwr 分别为前后车轮角速度 ;Fx f、Fx r、Fzf、Fzr分别为作用于前后车轮上的纵向力和垂向力;T bf、T br分别为作用于前后轮上的制动力矩。

根据图7中的整车纵向运动受力分析,可得到车辆在纵向运动过程中的运动微分方程：

式中,m为整车质量;Ax、cx分别为纵向迎风面积和风阻系数;ρ为空气密度。

图7 车辆纵向运动受力分析图

根据车轮纵向滑移率定义,得到前后车轮的转动角加速度：

将式(12)～式(16)进行整理,得到车辆加速度与发动机输出转矩之间的动力传动公式：

其中,mm、Tre分别为车辆的等效质量和等效阻力力矩,它们的计算公式为

2 自适应巡航控制系统设计

智能车辆自适应巡航控制系统是由上层加速度目标控制和下层伺服切换控制组成的综合控制系统,控制系统的结构如图8所示。

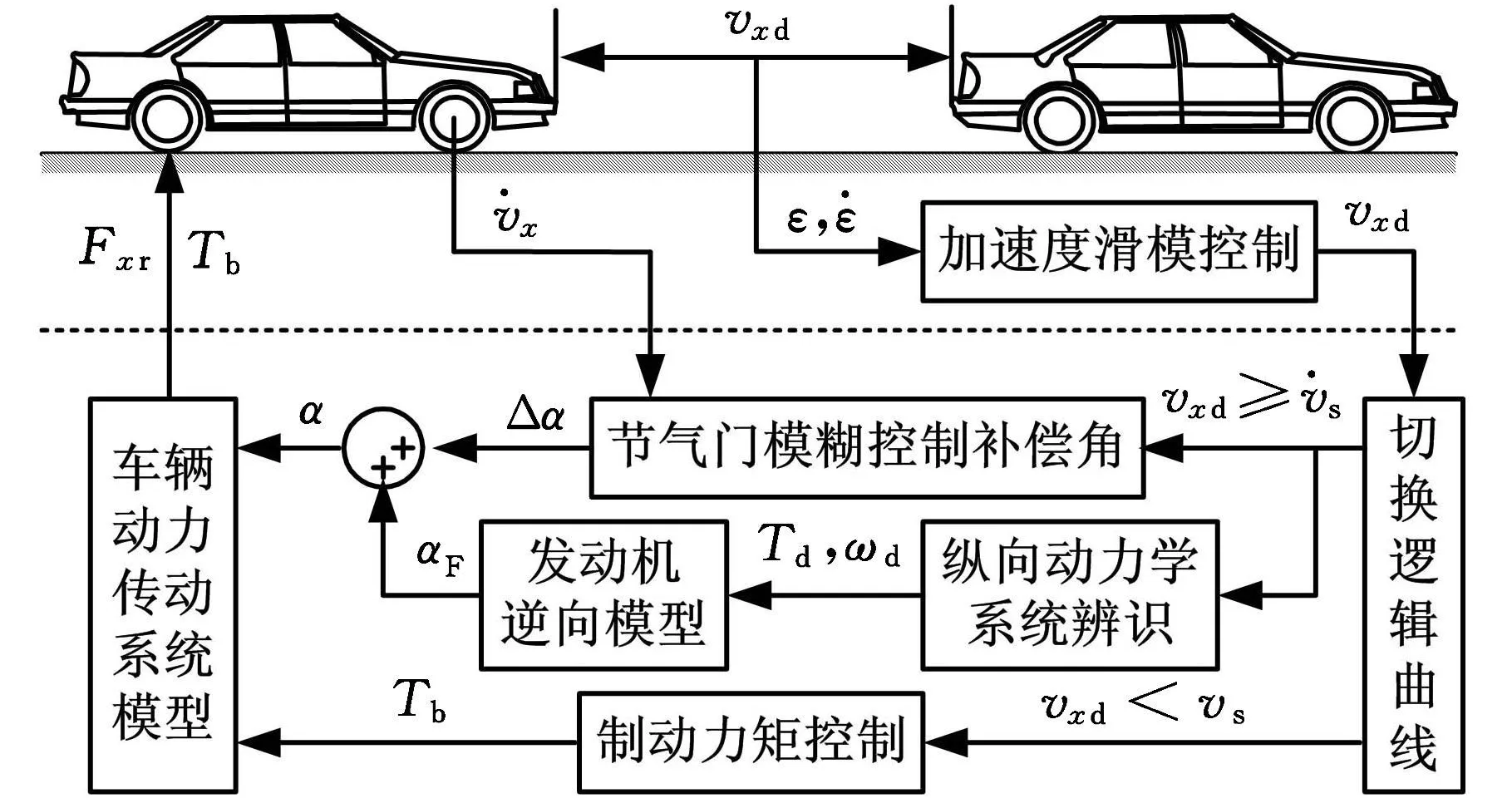
图8 自适应巡航控制系统原理示意图

2.1 上层控制器设计

车间相对距离误差是评价自适应巡航控制系统的一个重要指标,为了提高模型的控制精度,文中将车间相对速度误差作为控制系统的另一个指标。定义上层控制器的变量参数为

式中,ε、ε◦分别为车间相对距离误差和相对速度误差;H为车间相对距离期望值;L为车身长度;xh、x分别为引导车辆和被控车辆的纵向位置;vh为引导车辆的行驶速度。

根据滑模控制理论,选择自适应巡航控制的滑模切换面为

其中,λ1、λ2为滑模控制的两个参数,均为大于零,对式(23)求导得

选取合适的控制律,采用饱和函数sat(S)使滑模切换面S的一阶微分得以收敛,即

将式(25)代入式(24),得到被控车辆的期望加速度：

2.2 下层控制器设计

2.2.1 节气门开度前馈控制

当车辆处于稳态行驶工况时,纵向行驶速度与发动机的转矩和转速之间存在对应关系。根据上层控制器得到的期望加速度,利用系统辨识技术反求出稳态行驶工况下的发动机期望转矩T d和期望转速n d,然后利用发动机逆向模型获得节气门的前馈控制开度αF：

发动机逆向模型的节气门开度特性如图9所示。

图9 发动机节气门开度特性

稳态行驶工况下,发动机转矩与车辆行驶速度之间的关系曲线如图10所示,对式(17)进行整理,得到期望发动机转矩T与期望加速度之间的函数关系：

图10 动力传动系统逆向转矩特性

稳态行驶工况下,发动机转速与车辆行驶速度之间的关系曲线如图11所示,期望发动机转速n d可表示为以期望速度vx d和驱动轮纵向滑移率sx r为变量的函数：

图11 动力传动系统逆向转速特性

2.2.2 节气门开度反馈补偿

采用模糊控制器对节气门开度进行反馈补偿,前馈控制和反馈补偿共同作用,使下层控制器达到跟踪期望加速度的目的。选取被控车辆实际速度与期望速度之间的误差Δv及其变化率Δa作为模糊控制器的输入信号,以k in、k ic为输入信号的增益参数,模糊控制器输出信号为发动机的节气门开度补偿角Δα。模糊控制器的输入信号定义为

对于输入变量而言,采用5个模糊语言子集来确定,即{NB,NM,ZO,PM,PB},输入变量论域为{-2,2};对于输出变量,采用7个模糊语言子集来确定,即{NB,NM,NS,ZO,PS,PM,PB},输出变量论域为{-3,3}。输入变量和输出变量的模糊子集采用等腰三角形隶属度函数,表达模糊控制器输入、输出变量之间关系的三维曲面如图12所示。

图12 模糊控制输入、输出变量曲面

参考专家经验,并依据车辆传动系统的动力学特性,确定模糊控制规则的选取原则如下：

(1)当速度误差和加速度误差都较大时,车辆处于行驶工况快速变化状态,应该产生较大的节气门开度补偿角,反馈补偿与前馈控制共同作用,快速改变作用于被控车辆上的力矩,从而有效提高跟踪期望加速度的响应速度。

(2)当速度误差和加速度误差其中一个较大时,被控车辆处于瞬态和稳态的过渡阶段,应产生较小的节气门开度补偿角,协调误差超调量与响应快速性之间的矛盾,缩短控制过程的过渡时间。

(3)当速度误差和加速度误差都较小时,车辆处于稳态行驶工况,前馈控制能够较好地完成跟踪期望加速度的任务,应尽量减小节气门开度补偿角,避免在平衡位置产生振荡,提高自适应巡航控制系统的稳定性。

根据上面选取原则及模糊子集数量,确定25条模糊控制规则,如表1所示。

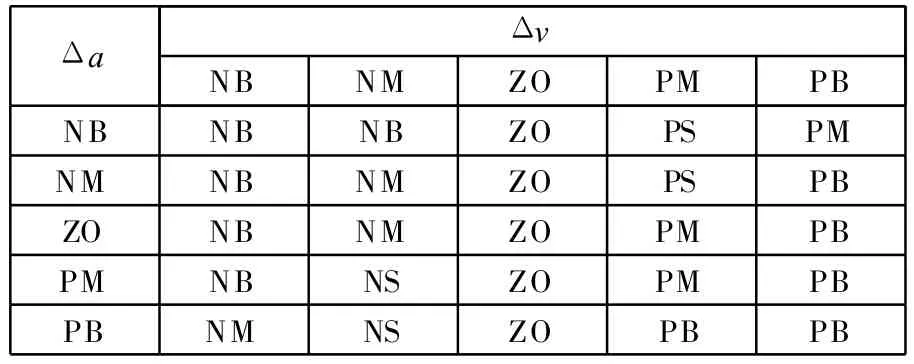
表1 反馈补偿模糊控制规则

为了在模糊判决过程中增强过渡性,并防止控制量发生跳跃,利用重心法进行模糊判决计算,模糊控制器的输出信号为发动机的节气门开度补偿角Δα,kα为输出信号的增益,下层控制器的节气门开度变为

2.2.3 节气门 /制动器切换逻辑

在实际行驶过程中,同时对节气门和制动器进行控制可能会导致系统振荡和性能冲突。因此,要根据期望加速度确定节气门/制动器控制的切换逻辑曲线[12],该曲线表现为节气门开度最小时不同挡位的车辆纵向加速度v◦s,它的大小由发动机倒拖力矩、各挡位变速比、滚动阻力及迎风阻力确定：

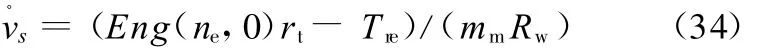
其中,Eng(n e,0)为节气门开度最小时的发动机倒拖力矩。在不同行驶速度情况下,根据式(34)得到的切换逻辑曲线如图13中的实线所示。

图13 节气门/制动器切换逻辑曲线

为了在巡航控制过程中提高车辆的驾乘舒适性和部件可靠性,在切换逻辑曲线上下两侧各添加宽度为h的缓冲层,如图13中的虚线所示,文中取h=0.02m/s2。定义优化后的切换逻辑规律如下＞h时,控制节气门,关闭制动器;≤h时,节气门、制动器状态保持;＜-h时,控制制动器,节气门最小。

通过控制制动器压力pbr,产生期望制动力矩Tb用于补偿期望加速度与切换加速度之间的差值：

3 仿真研究

在路面附着系数μr=0.8的道路上对智能车辆的自适应巡航控制效果进行仿真研究,同时,与仅采用节气门开度反馈补偿控制时的纵向运动仿真结果进行性能比较。仿真过程被分为加速行驶、车辆跟踪和制动减速三种工况,仿真环境及车辆模型参数如表2所示。

表2 自适应巡航控制仿真参数

假设三种仿真工况下的车辆理想加速度曲线如图14所示。

图14 理想加速度曲线

3.1 加速行驶工况

假设道路前方没有引导车辆行驶,被控车辆以期望加速度从静止加速到巡航速度35m/s,期望加速度如图14中0～45s的曲线所示。由于车辆在加速行驶工况下传动比不断发生变换,如图15a所示,这使发动机和液力变矩器的非线性特性变得非常明显。利用自适应巡航控制系统对节气门开度进行前馈-反馈综合控制,如图15b中实线所示,该系统能够在强非线性的加速行驶工况下快速消除由于挡位变换造成的扰动误差;而单独采用节气门开度反馈补偿控制时,如图15b中虚线所示,虽然在挡位固定时段可以取得较好的控制效果,但是,根据挡位变换时刻的仿真试验数据可知,被控车辆的加速度和相对速度误差的最大绝对值分别比前馈-反馈综合控制时的最大绝对值增加了48.39%和51.22%,如图15c和图15d所示。这表明文中设计的自适应巡航控制系统具有较好的适应性。

3.2 车辆跟踪工况

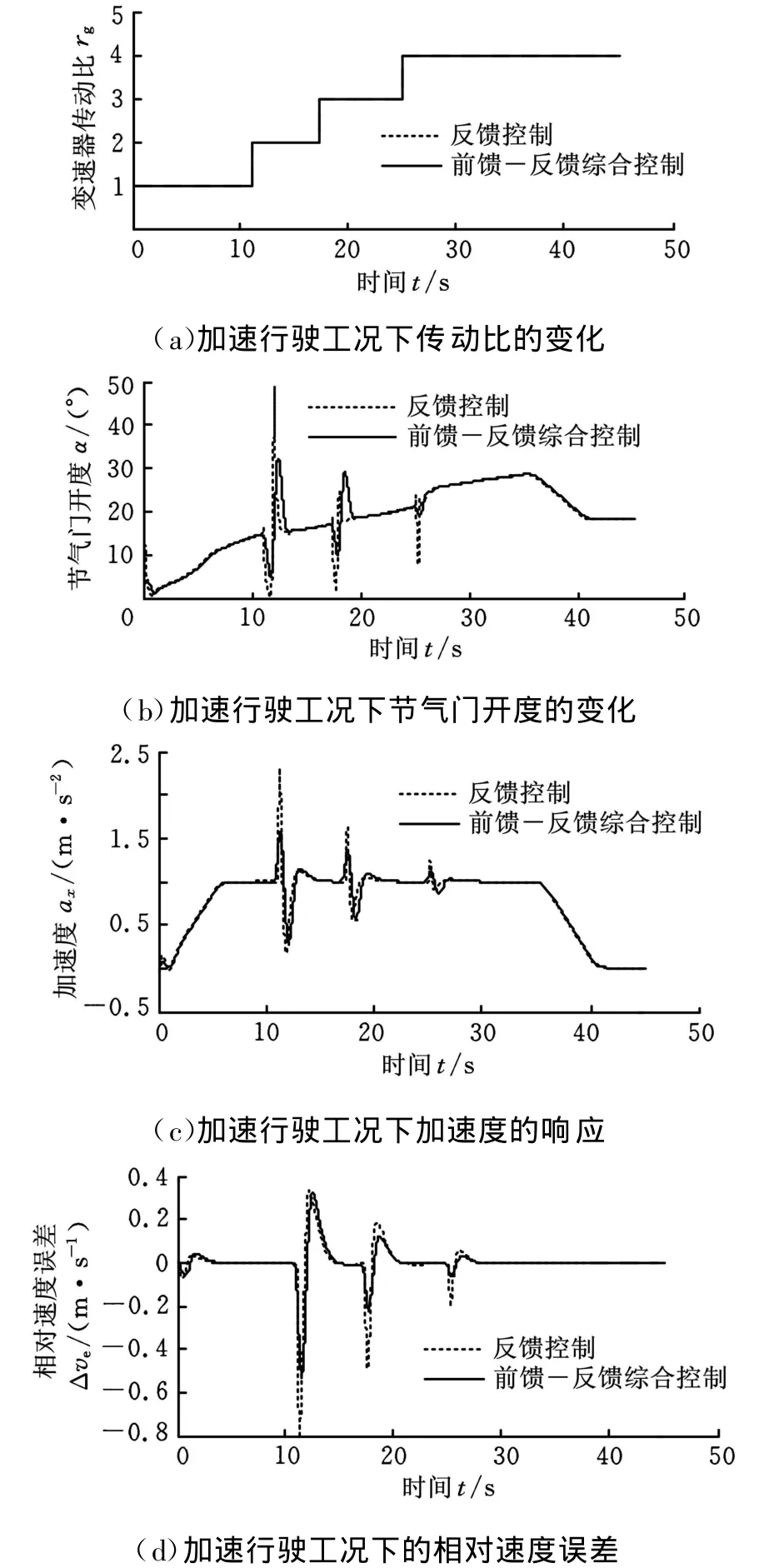
图15 加速行驶工况仿真结果

假设引导车辆在该工况下的加速度如图14中45～105s的曲线所示,被控车辆以恒定间距3.5m跟踪引导车辆行驶。对该工况下的仿真结果分析可知,自适应巡航控制系统作用下的相对间距误差和相对速度误差均被控制在较小范围之内,其最大值与仅采用节气门开度反馈控制时的相应最大值相比,分别降低了5.4%和42.86%,且跟踪误差受引导车辆加/减速度变化的影响较小,具有较高的控制精度,如图16a和图16b所示。另外,由于该工况下的速度变化相对较小且没有挡位变换,主要采用节气门开度前馈控制实现智能车辆的自适应巡航功能。从图16c可以看出：该工况下的节气门开度控制量平滑、稳定,能够有效提高自适应巡航控制系统的驾乘舒适性;而仅采用节气门开度反馈控制时,节气门开度的控制量出现了振荡现象,不利于节气门执行器的操作。仿真结果表明,文中设计的自适应巡航控制系统能够降低车辆跟踪工况下的跟踪误差,提高被控车辆的跟踪精度。

图16 车辆跟随工况仿真结果

3.3 制动减速工况

假设引导车辆的期望减速度如图14中105～150s的曲线所示,自适应巡航控制系统应防止被控车辆与引导车辆发生碰撞。从开始制动到118s时,主要通过控制节气门开度改变传递到驱动轴上的驱动力矩,使被控车辆达到期望减速度,如图17a所示;从118s到被控车辆停止,则通过控制制动液压产生制动力矩,制动力矩与发动机倒拖力矩共同作用,使被控车辆达到期望减速度,如图17b所示。该时段的节气门开度为零,因此,两种控制系统作用下的相对速度和间距误差主要取决于上层控制器得出的期望减速度。在自适应巡航控制系统作用下,自动变速器的传动比变换情况如图17c所示,随着传动比不断变小,发动机倒拖力矩的传递比率就会越来越大。根据制动减速工况下的仿真试验数据可知：自适应巡航控制系统作用下的车间相对速度误差的最大值为-0.098m/s,比仅采用节气门开度反馈控制时的最大误差值减小了30%,如图17d所示,说明控制切换过程平顺、稳定,不会产生过大的纵向冲击力;该工况下的最大相对间距误差为-0.152m,与仅采用节气门开度反馈控制时的控制效果相比,最大误差减小了22.84%,如图 17e所示,远小于两车之间的初始间距3.5m,保证了车辆在制动减速工况下的主动安全性。

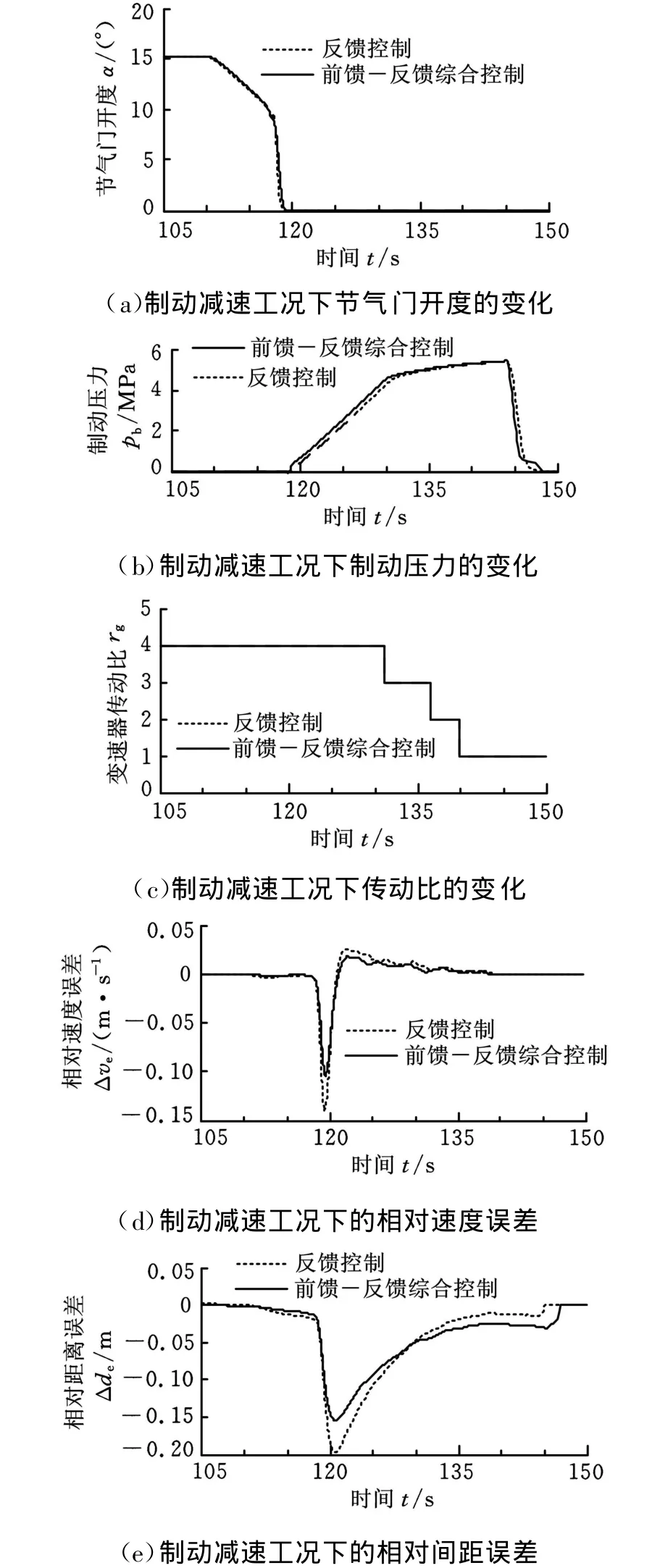
图17 制动减速工况仿真结果

4 结论

(1)由发动机、液力变矩器、自动变速器和非线性轮胎模型共同组成的车辆动力传动系统模型与实际车型的结构特点相一致,能够较真实地反映出车辆纵向动力学的非线性时变特性,可满足智能车辆自适应巡航控制对动力传动系统模型的要求。

(2)自适应巡航控制系统能够对被控车辆的节气门开度和制动力矩进行前馈-反馈综合控制,并且,设计的切换逻辑曲线考虑了挡位变换的影响。该系统能够有效减小自适应巡航控制过程中的相对速度误差和间距误差,提高了智能车辆在各种行驶工况下的跟踪性和适应性。

(3)从自适应巡航控制过程的仿真结果可以看出,较大的相对速度误差和间距误差均发生在换挡时刻或节气门/制动器控制切换时刻。因此,在今后的研究工作中,深入分析自动变速器换挡品质及切换逻辑曲线对车辆纵向动力学的影响,以提高自适应巡航控制精度,改善系统跟踪性能。

[1] Vahidi A,Eskandarian A.Research Advances in Intelligent Collision Avoidance and Adaptive Cruise Control[J].IEEE Transactions on Intelligent Transportation Systems,2003,4(3)：143-153.

[2] Li Li,Wang Feiyue.Advanced Motion Control and Sensing for Intelligent Vehicles[M].New York：Springer,2007.

[3] Marsden G,McDonald M,Brackstone M.Towards an Understanding of Adaptive Cruise Control[J].Transportation Research Part C：Emerging Technologies,2001,9(1)：33-51.

[4] Guanguli A,Rajamali R.Tractable Model Development and System Identification f or Longitudinal Vehicle Dynamics[J].Proceedings of the Institution of Mechanical Engineers,Part D：Journal of Automobile Engineering,2004,218(10)：1077-1084.

[5] Jarrah M A,Shaout A.Fuzzy Modular Autonomous Intelligent Cruise Control(AICC)System[J].Journal of Intelligent and Fuzzy Systems,2001,11(3/4)：121-134.

[6] 李以农,郑玲,谯艳娟.汽车纵向动力学系统的模糊-PID控制[J].中国机械工程,2006,17(1)：99-103.

[7] Lee G D,Kim S W.A Longitudinal Control System for a Platoon of Vehicles Using a Fuzzy-sliding Mode Algorithm[J].Mechatronics,2002,12(1)：97-118.

[8] Bin Yang,Li Keqiang,Ukawa H,et al.Nonlinear Disturbance Decoupling Control of Heavy-duty Truck Stop and Go Cruise System[J].Vehicle System Dynamics,2009,47(1)：29-55.

[9] Nouveliere L,Mammar S.Experimental Vehicle Longitudinal Control Using a Second Order Sliding Mode Technique[J].Control Engineering Practice,2007,15(8)：943-954.

[10] Yi J,Wang X L,Hu Y J,et al.Modeling and Simulation of a Fuzzy Controller of Automatic Transmission of a Tracked Vehicle in Complicated Driving Conditions[J].Proceedings of the Institution of Mechanical Engineers,Part D：Journal of Automobile Engineering,2007,221(10)：1259-1272.

[11] Hirschberg W,Rill G,Weinfurter H.User-appropriate Tyre-modeling for Vehicle Dynamics in Standard and Limit Situations[J].Vehicle System Dynamics,2002,38(2)：103-125.

[12] 李贻斌,阮久宏,李彩虹,等.智能车辆的纵向运动控制[J].机械工程学报,2006,42(11)：94-102.