基于DDS的低通滤波器设计与仿真
2010-06-03张海涛庞永星
苗 圃,张海涛,庞永星
(河南科技大学 电子信息工程学院,河南 洛阳471003)
DDS[1]作为一种全数字器件,由于自身特性,其输出频谱杂散是制约其发展应用的一个瓶颈。为了获得高质量纯净的波形信号输出,使用低通滤波器去除干扰信号非常重要。在整个DDS实现过程中,低通滤波器不仅要滤出高频信号,还要去除DDS的谐波杂散和边带杂散信号,因此低通滤波器是信号发生器中信号处理的重要部件,其性能的优劣对输出波形信号有重大影响。
1 DDS信号发生器
DDS信号发生器的基本工作原理如图1所示,DDS一般由4部分组成:N位相位累加器,波形存储ROM,D/A转换器和低通滤波器。在参考时钟fC的控制下,相位累加器在fC上升沿对频率控制字K进行累加,累加结果作为相位编码对波形ROM里存储的幅值进行寻址,输出的二进制幅值编码进行数模转换后,经过低通滤波得到平滑曲线。相位累加器加满到2N产生溢出后,则产生一个周期的波形。DDS输出频率:
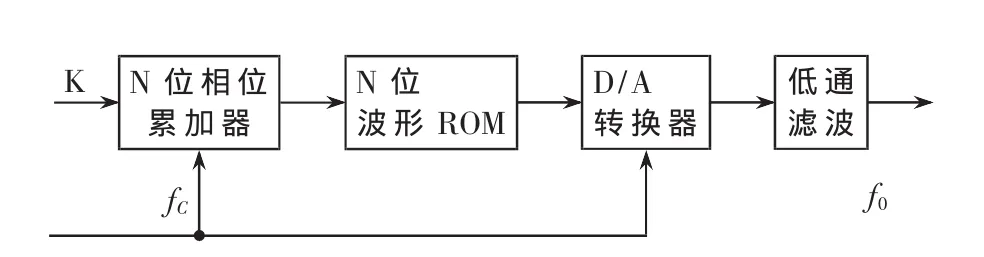
图1 DDS信号发生器工作原理框图

在fC为定值情况下,DDS的输出频率由控制字K和相位累加器位数N决定,当K=1时,最小分辨率:

DDS输出频谱如图2所示,实际情况下DDS输出大量的杂散信号,杂散主要落在信号主频谱附近,以边带形式出现,影响大且难于去除。
由奈奎斯特采样定理可知,理论上输出信号的频率是DDS系统时钟fC的50%,但是,为了得到较好的输出杂散性能,工程上一般取系统时钟作为设计低通滤波器的通带截止频率。本文DDS信号发生器采用的AD9852是一款性能优越的DDS集成芯片,内置一个高速、高性能数模转换器,共同构成一个数字可编程、捷变频率合成器,它以300 MHz精密时钟源作为基准时钟,可产生一个高度稳定的频率、相位和振幅可编程的余弦波形输出。由奈奎斯特采样定理可得到AD9852的最高输出频率高达150 MHz,但为了保证高质量波形输出,设计低通滤波器的截止频率为120 MHz。

2 低通滤波器设计
2.1 滤波器分类
滤波器[2]是无线电技术中许多设计问题的中心,用其分开或组合不同频率的信号,其作用是从复杂的信号中提取所需信号,抑制不需要的信号。对已知激励在时域或频域产生规定响应的网络,对有用信号尽量无失真放大,对噪声尽量衰减。衡量滤波器的技术指标主要有3种:通带、阻带和过渡带。理想状态下过渡带增益为0,但是在物理上是不可实现的,通常情况下要求过渡带越短越好。
滤波器的种类多,根据其输入输出信号的形式,大体可以分为模拟滤波器和数字滤波器两类,模拟滤波器又可以分为无源滤波器和有源滤波器。根据滤波器幅频特性可以分为低通、高通、带通和带阻滤波器。
2.2 滤波器选择

由于有源滤波器主要用于低频场合且受到放大器开环增益不够和频带限制,本文所要设计的低通滤波器的截止频率为120 MHz,因此采用无源低通滤波器。工程中经常采用一个可实现的衰减特性来逼近理想特性,使衰减的变化处在规定的容限之内[3]。根据不同的逼近原则和衰减特性来选择不同频率响应的滤波器。常用的低通滤波器按其传递函数不同可以分类为:巴特沃斯滤波器、切比雪夫I滤波器、切比雪夫 II、贝塞尔滤波器和椭圆滤波器。当阶数N=8时其在Matlab环境下幅频仿真图如图3所示。巴特沃斯滤波器拥有最平滑的幅频响应,频率响应单调下降,通带内比较平坦,截断频率处有3 dB的衰减,但在阻带衰减缓慢,从通带到阻带的过渡带很宽,对带外干扰信号衰减作用很弱。切比雪夫I型滤波器通带内具有等波纹起伏特性,阻带内单调下降且具有更大的衰减,截止特性好但群延迟特性不好。切比雪夫分布II型滤波器与切比雪夫I型频带特性刚好相反,通带内平滑且有衰减特性,阻带内有等波纹起伏特性。贝塞尔滤波器在零频时具有最平坦的群延时,群延迟在整个通带内保持不变,但是截止特性相当差。椭圆型滤波器在通带内和阻带内都有等波纹的起伏,比巴特沃斯和切比雪夫滤波器有更陡的下降梯度,过渡带陡峭,在相同性能指标下,椭圆滤波器所需的阶数更小。综合比较后,椭圆滤波器的性能更好。因此本文设计采用椭圆型滤波器。
2.3 椭圆型低通滤波器设计方案
椭圆函数滤波器[4]又叫考尔(Cauer)滤波器,它的传递函数在有限频率上既有零点又有极点,零极点在通带内产生等波纹,但零点在阻带内减小了过渡区,因此可以得到陡峭的衰减曲线。椭圆函数滤波器的传递函数为:

其
中,ε为波纹参数,En(Ω)为 n阶椭圆函数,用零极点式可表示为:



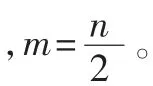
滤波器的设计要根据滤波器的通带最大衰减RP或通带边界反射系数ρ、阻带最小衰减RS和选择因子K确定其介数n,然后根据相应的曲线和归一化的元件值,得到去归一化后实际的元件值。参数RP、RS、K和n知道其中3个就可以求出另1个。它们之间存在特定的关系[3]可以近似表示为:


本文椭圆型低通滤波器的设计指标主要有:
(1)通带截止频率WP=120 MHz;
(2)通带内最大衰减系数RP=0.2 dB;
(3)阻带截止频率WS=135 MHz;阻带内最小衰减系数RS=66 dB;
(4)电路输入输出匹配阻抗R1=R2=50 Ω;
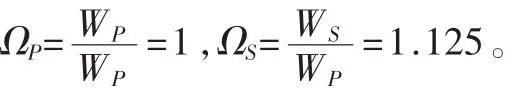

图4 椭圆滤波器电路拓扑结构

其中,L′、C′为去归一化的元件值,fFS为频率标度系数,可以直接用2πfC表示。Z为阻抗标度系数即Z=50。代入计算后各个元件值如表1所示。
表1 元件值表
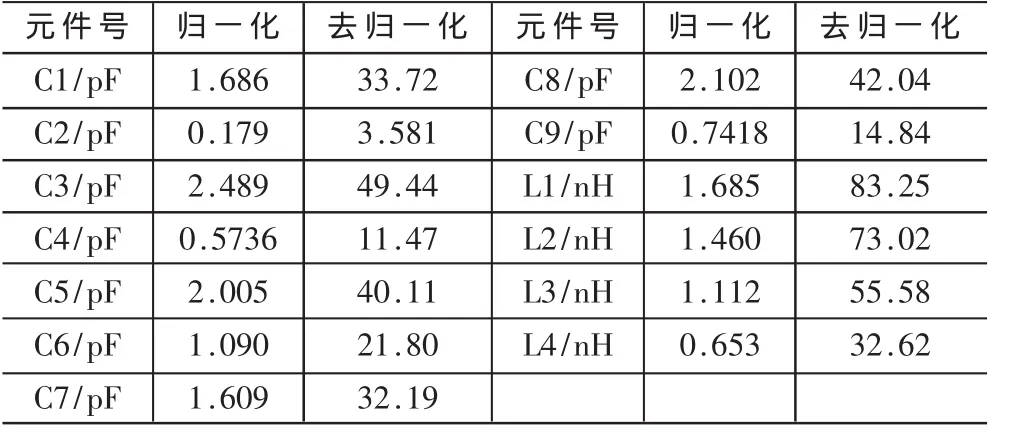
元件号C1/pF C2/pF C3/pF C4/pF C5/pF C6/pF C7/pF归一化1.686 0.179 2.489 0.5736 2.005 1.090 1.609去归一化33.72 3.581 49.44 11.47 40.11 21.80 32.19元件号C8/pF C9/pF L1/nH L2/nH L3/nH L4/nH归一化2.102 0.7418 1.685 1.460 1.112 0.653去归一化42.04 14.84 83.25 73.02 55.58 32.62
3 电路仿真
表1所列的元件为理想情况下计算得出的值,实际情况下元件公司并不能提供如此精确的元件值。因此,根据实际情况适当修改元件值,尽量选择比较接近的值,使所设计滤波器的幅频特性接近理想滤波器的幅频特性。
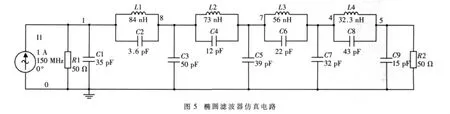
为了检验滤波器是否达到设计指标,本文采用Multisim 10来进行电路仿真,以便直观地看到滤波器的幅频特性。滤波器仿真电路如图5所示。信号源频率分别为 135 MHz、150 MHz和 100 MHz时滤波器输入输出对比如图6、图7和图8所示,顶部为滤波器输入信号波形,底部为滤波器输出信号波形。从图6中可以看出滤波器输出信号在0~150 ns时处于震荡衰减期,150 ns以后输出信号幅度逐渐趋近于平衡点。从图7中可以看出滤波器输出信号在0~100 ns之间处于震荡衰减,100 ns后输出信号幅度趋于平衡点。图8可以很好地体现低通滤波器的通带特性,100 MHz信号能够全部无衰减通过,但是有10 ns左右的延时输出。
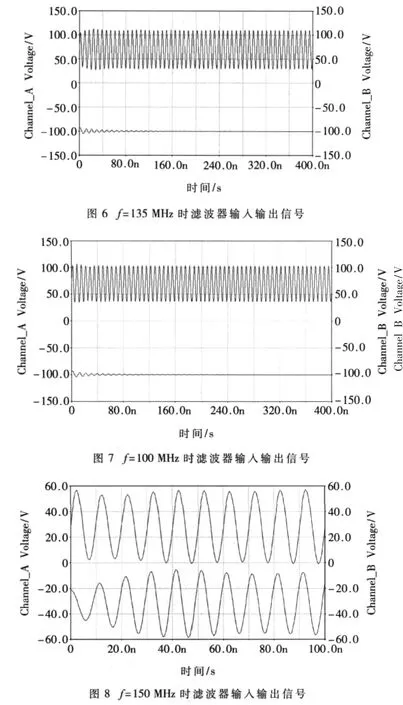


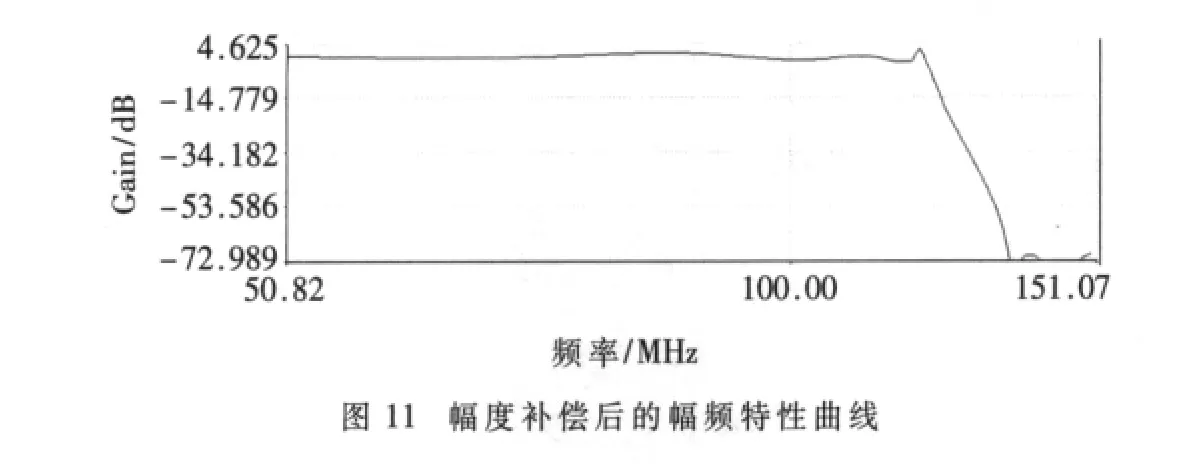
仿真后可以看出具有陡峭的截止特性,幅频特性良好,但在截止频率处有细微偏移。最后根据幅频特性仿真图在椭圆滤波器电路最后一级加入幅度补偿电路后,能够极好地满足截止频率为120 MHz、通带波纹小于0.2 dB、阻带最小衰减为66 dB的设计指标。在实际电路的制作中,由于没有完全理想的元件值,因此对元件值要适当调整后再进行仿真,直到能够达到或接近理想幅频特性为止。本文所使用方法可以适用于各个场合、各个频段的椭圆型低通滤波器的设计。
[1]KROUPA V F.Spectra properties of DDFS:computer simulation and experimental verifications[C].IEEE Proc.48th AFCS,1994:613-623.
[2]罗军辉,罗江,白义臣,等.Matlab7.0在数字信号处理中的应用[M].北京:机械工业出版社,2005.
[3]毛敏,郑珍,周渭.基于DDS的低通滤波器的设计与实现[J].电子科技,2006,3:17-20.
[4]阿瑟·B·威廉斯.电子滤波器设计手册[M].喻春轩,译.北京:电子工业出版社,1986.
[5]彭辉生,陈永泰.DDS信号发生器中椭圆低通滤波器的设计[J].电子元器件应用,2007,4(9):57-58.
[6]甘本袯,吴万春.现代微波滤波器的结构与设计[M].北京:科学技术出版社,1973.