扩散边墙内缓冲击波的初步计算

姬春利，樊有锋

（1.江西蓝天学院，江西 南昌 330098；2.西北农林科技大学，陕西 杨凌 712100）

水工明槽急流中，当边墙向水流外侧偏转时，由于水流失去边墙的依托，水面出现跌落，产生绕动，形成缓冲击波。早在20世纪30年代Von Karman首先推导得出缓冲击波积分式[1，2]，该积分式目前被各类教科书普遍采用，但由于该积分式较复杂，直接求解较困难，故常利用辅助曲线图进行求解[3]，但查图人为误差较大，且不便于应用，为解决卡门积分不易求解的困难，20世纪90年代刘韩生等人对缓冲击波的数值计算公式进行了研究，得出积分简化式，该简化式形式简单，便于应用，适用于一般的人工急流明渠[4]。

1 缓冲击波的计算

缓冲击波就是边墙向水流外侧偏转产生的水流扰动现象。如图1所示，在明渠扩散段中，河道偏转起始点为O，在O点以后河道向水流外侧偏转，偏转角为α（α＜0），即边壁偏转角。先假定来流为均匀流，流速记为v1，水深h1，来流弗如德数Fr1（Fr1＞1），计算缓冲击波的边界线 1，2，波后水深h。

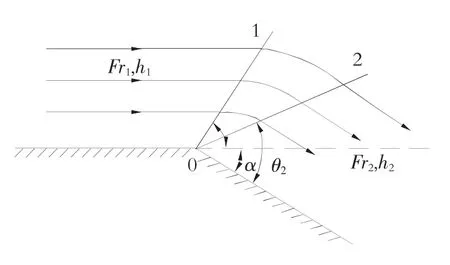
图1 缓冲击波示意图

1.1 冯·卡门积分式法

自20世纪30年代起，流体力学大师Von Karman（冯·卡门）的缓冲击波积分式[1，2]便一直被后人延用至今，并被许多教科书引用。

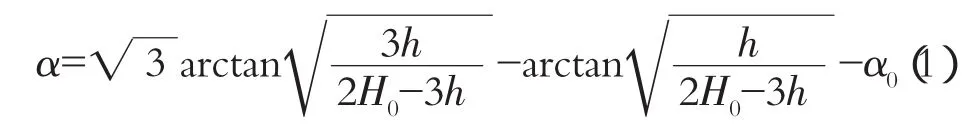
其中α0为积分常数。根据θ=0时h=h1的初始条件来决定。（Fr＞1）

计算步骤：

（2）根据水流初始条件，按（2）式计算出 α0，将

计算波后水流弗如德数Fr2；

1.2 刘韩生简化式法

刘韩生缓冲击波简化式是20世纪90年代末刘韩生等人根据Karman积分式，利用比能不变假定推导而来[4，5]。计算步骤：

计算出限制缓冲击波的第

一条干扰线的位置；

（2）根据（3）式计算波后水深 h2；

计算波后水

流弗如德数Fr2；

确定缓冲击波的下线位置。

2 计算及结果分析

假设来流水深h1=1m，来流弗如德数，边墙偏转角 α=（2～10°），分别利用刘韩生简化式和冯·卡门积分式计算缓冲击波的边界θ1，θ2，波后水深 h2，波后水流的弗如德数 Fr2，对两理论计算结果进行对比，刘韩生简化式计算的结果相对于冯·卡门积分式计算结果的偏差用表示，将二者计算结果比较可知：

（1）当 α 一定时 θ2，h2的值随的增大而减小，Fr2的值随的增大而增大；当一定时 θ2，h2的值随α的增大而减小，Fr2值随α的增大而增大。

（3）从计算过程来看：冯·卡门积分式法计算缓冲击波下边界θ2时，计算过程比较复杂，需要试算，应用相对不方便。利用刘韩生缓冲击波简化式法比较方便、简洁。

[1]C.M.斯里斯基著，毛世民，杨立信译.高水头水工建筑物的水力计算[M].北京：水利水电出版社，1984：113～135.

[2]Ve Te Chow.Open—channel Hydraulics[M].New York：Mc Graw—Hill Book Company，Inc.1959：448～454.

[3]Ippen，A.T.Mechanics of supercritical flow [J].Trans.ASCE，116，1951：326～346.

[4]刘韩生，倪汉根.急流冲击波简化式[J].水利学报，1999，（6）：61～65.

[5]倪汉根，刘亚坤.击波 水跃 跌水 消能[M].大连：大连理工大学出版社，2008：1～35.