铁道车辆制动系统防滑控制仿真与试验研究
2010-05-31左建勇任利惠吴萌岭
左建勇,任利惠,吴萌岭
(同济大学 铁道与城市轨道交通研究院,上海 200092)
目前,铁道车辆的制动方式主要依赖轮轨黏着,而黏着制动存在的最大缺陷就是黏着力有限.同时,轮轨黏着受轮轨间状态影响较大.在牵引或制动时,如果牵引或制动力矩过大就会使车轮空转或滑行甚至抱死.因此需根据不同的车速、载重、环境等条件对制动力进行控制.铁道车辆防滑系统的采用就是解决列车运行过程中滑行再黏着控制的有效手段之一,因此有必要对其进行仿真分析与研究[1-3].
1 单轮对制动动力学相关模型
1.1 轮对模型
制动状态下的轮对受力状态如图1所示.根据图1,轮对旋转时动力学方程如下:
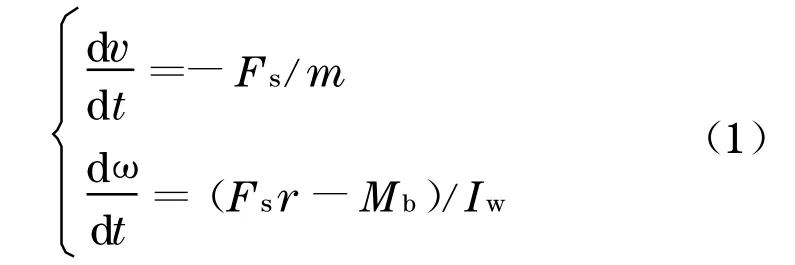
式中:v为轮对纵向运动速度;Fs为轮轨纵向蠕滑力;m为车轮上的质量;ω为轮对的转速;t为时间;r为车轮半径;Mb为制动力矩;Iw为车轮的转动惯量.

图1 制动状态下轮对受力图Fig.1 Force diagram of wheelset under brake state
在讨论制动系统防滑控制的轮对模型建立时,仅考虑轮对的旋转自由度和纵向自由度,不考虑轮对垂向和横向自由度.图2所示为制动状态下轮对运动学仿真模型,输入信号为Fs,Mb;输出为v,ω.

图2 制动状态下轮对运动学仿真模型Fig.2 Kinematics simulation model of wheelset under brake steate
1.2 蠕滑力模型
如图3a所示为轮轨蠕滑力Fs与蠕滑率S关系图.可以看出:随着S的增大,Fs存在一个最大值即饱和力;之后随着S的增大,轮轨间开始滑动.为了模拟出轮对纵向运动的黏着—滑行过程,这里对Fs与S关系图进行简化[4-5],如图3b所示.即采用分段线性化的计算模型,其数学表达式为
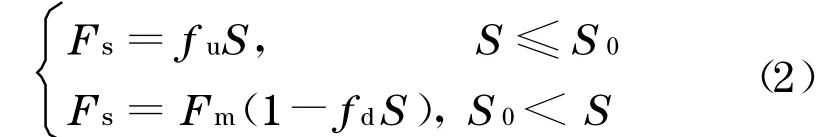
式中:fu为上升段蠕滑力系数;fd为下降段蠕滑力系数;S为蠕滑率,S=(v-rω)/v;r为车轮半径;S0为接触斑全滑动时的临界蠕滑率;Fm为最大蠕滑力;Fm=μ N;μ为黏着系数;N为车轮上的正压力.
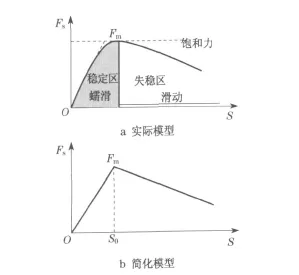
图3 轮轨蠕滑力和蠕滑率关系Fig.3 Relationship between creep force and creep ratio
通过Matlab建立的蠕滑力仿真模型如图4所示,输入为 v,ω;输出为 S,Fs.

图4 蠕滑力仿真模型Fig.4 Simulation model of creep force
1.3 制动力模型
制动力是轮对动力学方程中惟一的受控力.根据制动力的产生是否与轮对的转速相关,这里将制动力分为开环控制和闭环控制,其中防滑控制属于闭环控制.
1.3.1 开环控制
开环控制中,制动力的大小仅受制动指令控制,与车轮的转速无关,这时制动力表达式为

式中:μz为制动夹钳与制动盘(闸瓦与轮对)之间的摩擦系数;C为基础制动的制动系数,与活塞面积、制动倍率和制动力作用半径有关;P为制动缸压力,来自气路系统.
1.3.2 闭环控制
闭环控制中,制动力的大小与车轮的转速反馈有关,对转速反馈采用不同的控制策略构成了多种控制方法,其中最简单的一种是防滑控制的棒棒控制,规律如下:即首先设定一个期望的蠕滑率S0,当实际蠕滑率大于S0时,则对制动缸排气,减小制动力;当实际蠕滑率小于S0时,则对制动缸充气,增加制动力.当然应该设置一个死区,当蠕滑率处在该区范围内,既不充气也不排气.
通过Matlab建立的闭环控制制动力模型如图5所示,输入为初始压力P0,蠕滑率S;输出为制动力矩Mb.
2 防滑气路系统与控制策略仿真模型
2.1 防滑气路系统仿真模型
典型的防滑气路系统由制动缸、防滑阀等组成,其中防滑阀有充气、排气和保压3个工作位置,通过控制防滑阀的开闭可以实现对制动缸的充气、排气或保压功能.图6为防滑气动系统DSHplus仿真模型,仿真建模中为尽量减小中继阀对其仿真结果的影响,采用一个风缸代替中继阀输出[6-7].
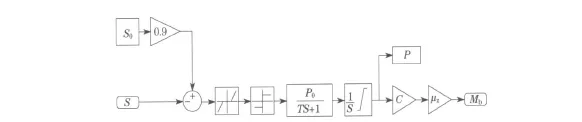
图5 制动力闭环控制仿真模型Fig.5 Simulation model of braking force closed loop control

图6 防滑气路组成及其DSHplus仿真模型Fig.6 Pneumatic path scheme and DSHplus model of anti-sliding system
2.2 防滑控制策略仿真模型
目前防滑阀的控制普遍采用在1次滑行过程中,多次高频排风的控制策略.因此在防滑气路的设计过程中,如何选择1次排气时间和排气次数2个关键参数尤为重要.为此建立了DSHplus仿真模型如图7所示,该模型可以较为方便地进行不同控制参数(如排气次数、排气时间等)的匹配选择[8].
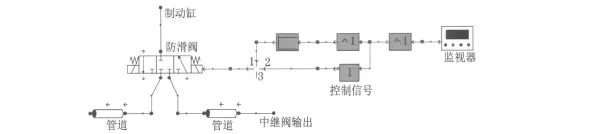
图7 防滑控制策略DSHplus仿真模型Fig.7 DSHplus simulation model of anti-sliding control strategy
3 仿真结果与分析
3.1 Simulink仿真结果
根据以上描述的数学模型,联合建立单轮对防滑控制Simulink仿真模型,选取仿真参数见表1.
图8给出了单轮对制动过程中在有无防滑控制作用下的仿真结果,图中虚线表示无防滑控制状况.
图8a给出了车辆的运动速度变化,可以看出在有防滑控制时,车辆的运动速度下降快于无防滑控制工况.图8b给出了轮对转速的变化,可以看出,无防滑控制时车轮的转速很快变为零,处于抱死状态,有防滑控制时车轮始终处于转动状态,而转速则在整个防滑控制过程中不断调整.图8c给出了制动距离的比较,可以看出有防滑控制时,制动距离小于无防滑的状态.图8d给出了制动缸压力的变化,可以看出在防滑控制时,制动缸压力在不断变化.

表1 轮对防滑仿真参数Tab.1 Simulation parameters of wheelset anti-sliding control
3.2 防滑气路仿真结果
当防滑阀的流量为5 L◦s-1时,防滑气动系统的进、排气特性如图9a所示.从图中看出在排气的初期阶段,相当于一个定容容器向外排气;在充气的最后阶段,相当于向一个定容容器充气.

图8 制动工况下单轮对有无防滑控制仿真结果Fig.8 Simulation comparison of wheelset anti-sliding under brake state
图9b为防滑阀排气、充气和保压过程控制策略的仿真结果,图中曲线分别表示了制动压力变化趋势和防滑阀排风、充气和保压的控制信号变化.由图可知:当制动缸压力为500 kPa时,每次排气20 ms,制动缸压力第1次下降约20 kPa,第2次、第 3次压力下降约30 kPa.通过改变仿真模型中排气时间、排气次数等参数,可以模拟防滑阀的气路特性,为防滑系统的设计提供理论依据.

图9 防滑气路系统及控制策略仿真Fig.9 Simulation of anti-sliding valve characteristic and control strategy
4 试验
结合上述关于铁道车辆制动系统防滑控制仿真结果,研制成功防滑控制单元,系统实物及试验装置如图10所示.

图10 防滑系统实物及试验装置Fig.10 Anti-sliding system and test equipment
图11所示为防滑阀排气特性试验,可以看出:当制动缸初始压力为 500 kPa时,每次排气约20 ms,制动缸压力第1次下降约20 kPa,第2次、第3次压力下降均为30 kPa左右,与上述仿真结果基本相符.
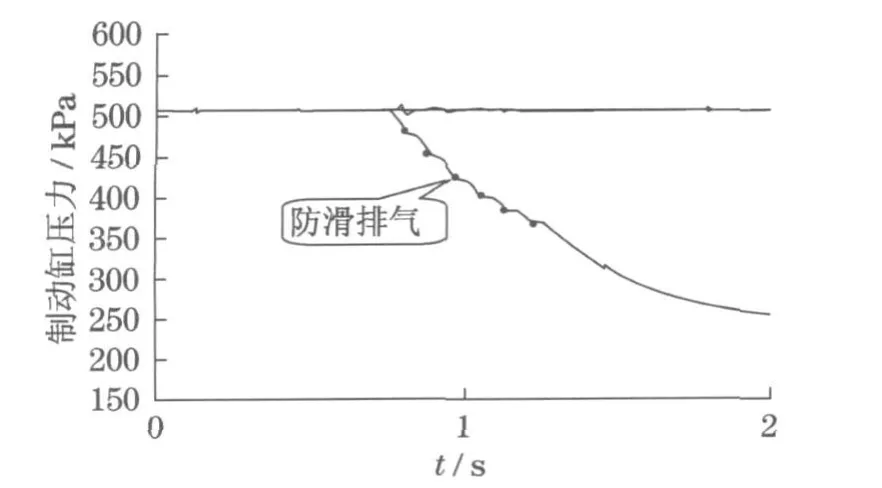
图11 防滑阀排气特性试验Fig.11 Discharge characteristic test of anti-sliding valve
图12为防滑控制策略验证试验,由于实际轮轨滑行状态很难模拟,试验中采用模拟轴速变化的方式进行验证:即设定一个基准速度并以恒定减速度下降,然后改变另一轴的速度变化,通过采集制动缸压力变化来验证防滑控制性能.由图可见:当速度差或减速度满足设定防滑控制阈值时,通过控制防滑阀的排气或充气时间,调整制动缸的压力大小,从而实现防滑控制目的.

图12 防滑控制策略试验结果Fig.12 Test of anti-sliding control strategy
5 结语
(1)针对铁道车辆制动系统防滑控制,可通过Matlab等软件建立其仿真模型并进行计算机仿真,为防滑控制单元的设计提供支撑.
(2)采用DHSplus软件建立防滑气路系统模型,可有效模拟和分析防滑控制过程的气路特性,并为防滑控制策略的参数选择提供参考.
(3)通过建立的防滑控制仿真模型,研制成功制动系统防滑单元,并进行了静止试验,结果表明该防滑系统满足设计要求,大大提高了制动系统防滑单元的设计开发周期.
(4)实际的轮轨防滑状态很难模拟,本文通过搭建试验装置,通过模拟轴速变化,能有效模拟滑行过程,进而开发和验证防滑控制算法.
[1] 任利惠,裴玉春,左建勇,等.截止式气动中继阀的数学模型和仿真[C]∥第 1届中日制动技术论坛.上海:同济大学,2008:75-81.
REN Lihui,PEI Yuchun,Z UO Jianyong,et al.Modeling and simulation ofpneumaticrelayvalves[C]∥Sino-Japanese Workshop on Train Braking Press.Shanghai:T ongji University,2008:75-81.
[2] Suh M W,Park Y K,Kwon S J.Braking perfo rmance simulation for a tractor-semitrailer vehicle with an air brake system[J].Journal of Automobile Engineering,2002,216(1):43.
[3] Chol J J,Park S H,Kim J S.Dy namic adhesion model and adaptive sliding mode brake control system for the railway rolling stocks[J].Journal of Rail and Rapid Transit,2007,221(3):313.
[4] Wang X D,Hu Y J,Li C G,et al.Modelling and analysis of an air-over-hydraulic brake system[J].Journal of Automobile Engineering,2004,218(8):805.
[5] 罗仁,曾京.铁道车辆防滑控制仿真[J].机械工程学报,2008,44(3):29.
LUO Ren,ZENG Jing.Anti-slidingcontrolsimulation of railway vehicle braking[J].Chinese Journal of Mechanical Engineering,2008,44(3):29.
[6] 魏伟,李文辉.列车空气制动系统数值仿真[J].铁道学报,2003,25(1):38.
WEI Wei,LI Wenhui.Simulation model of train brake system[J].Journal of the China Railway Socirty,2003,25(1):38.
[7] 耿志修,李学峰,张波.大秦线重载列车运行仿真计算研究[J].中国铁道科学,2008,29(2):88.
GENG Zhixiu,LI Xuefeng,ZHANG Bo.Simulation study of heavy haul train operation on Datong-Qinghuangdao railway[J].Chinese Railway Science,2008,29(2):88.
[8] 李成功,和彦森.液压系统建模与仿真分析[M].北京:航空工业出版社,2008.
LI Chenggong,HE Yansen.Modeling and simulation analysis of hydraulic system[M].Beijing:Aviation Industry Press,2008.
