一种基于启发式演化算法的最优-最差蚂蚁系统

李康顺 ，徐福梅，张文生，汤铭端

(1. 江西理工大学 信息工程学院，江西 赣州，341000；2. 华南农业大学 信息学院，广东 广州，510642；3. 中国科学院 自动化研究所，北京，100190；4. 航天科工集团 第二研究院，北京，100854)

蚁群算法最初是由意大利学者Dorigo等[1-3]提出，它是一种模拟昆虫王国中蚂蚁群体智能行为的仿生优化算法，具有较强的鲁棒性、优良的分布式计算机制、易于与其他方法相结合等优点。这种作为一种近年提出的新型优化算法，还没有像遗传算法、模拟退火算法等那样形成系统的分析方法和坚实的数学基础，许多问题如算法搜索时间较长、在运行过程中容易出现收敛过早或停滞现象、不能扩大解的搜索范围等[4-8]有待解决。针对这些缺陷，近年来国内外学者对蚁群算法提出大量的改进方法[9-13]，如Dorigo提出的Ant colony system (ACS)[1-2]，由 Stutzle和 Hoos提出的Max-min ant system(MMAS)[3]以及李士勇等[4]提出的最优-最差蚂蚁系统Best-worst ant system(BWAS)，这些改进算法对提高蚂蚁系统(AS)的计算性能起到一定的促进作用。目前，人们对蚁群算法的研究已经由最初单一的旅行商问题(TSP)领域渗透到了多个应用领域，由解决一维静态优化问题发展到解决多维动态组合优化问题。对这种算法的研究结果表明，它具有广阔的发展前景和实用价值[14-15]。在此，本文作者在最优-最差蚂蚁系统的基础上提出一种基于启发式演化算法的最优-最差蚂蚁系统。

1 旅行商问题(TSP)

旅行商问题(TSP)就是指给定 n个城市和两两城市之间的距离，要求确定1条经过各城市当且仅当1次的最短路线。其图论描述为：给定图G=(V, A)，其中V为顶点集，A为各顶点相互连接组成的边集，已知各顶点间的边接距离，要求确定 1条长度最短的Hamilton回路，即遍历所有顶点当且仅当1次的最短回路。

TSP是典型的易于描述却难以大规模处理的NP-hard问题，研究如何有效地解决TSP具有重要的理论意义和应用价值。研究TSP的方法有很多，如穷举搜索法、贪婪法、神经网络算法和遗传算法等，它们都存在求解效率低、搜索时间长，不能利用反馈信息等缺点。蚁群算法是最早应用到求解TSP的一种方法，具有分布计算、信息正反馈和启发式搜索的特征，是进化算法中一种新型的启发式优化算法。但是，它同样存在一些缺点，如算法搜索时间较长、运行过程中容易出现收敛过早或停滞现象、不能扩大解的搜索范围等。受演化算法的启发，在最优-最差蚂蚁系统的基础上，本文作者提出一种基于启发式演化算法的最优-最差蚂蚁系统(IEABWAS)来求解复杂TSP的算法，一方面，在该算法中加入启发式演化算子，在每次迭代中将最优蚂蚁与次优蚂蚁执行启发式交叉操作，并将这种使用启发式演化操作产生的更优个体替代系统中的最差蚂蚁，以达到快速收敛的目的；另一方面，将最优-最差蚂蚁的更新方式进行适应性调整，使搜索更加集中于最优解附近，从而提高算法的全局搜索能力。

2 蚁群算法

设有n个城市组成的集合C[6]，蚂蚁数目为m，用di,j(i, j=1, 2, …, n)表示城市i和城市j之间的距离，τij表示在t时刻城市i和城市j之间的路径上的残留信息素强度，以此来模拟实际蚂蚁的分泌物。蚂蚁 k(k=1, 2, …, m)在运动过程中，根据各条路径上的信息量决定其转移方向，同时用禁忌表tabuk(k=1, 2, …, n)来记录蚂蚁k当前所走过的城市，集合随着tabuk进化过程进行动态调整。在搜索过程中，蚂蚁根据各条路径上的信息量及路径的启发信息来计算状态转移概率。P表示在t时刻蚂蚁k由城市i转移到城市j的状态转移概率，其表达式为：

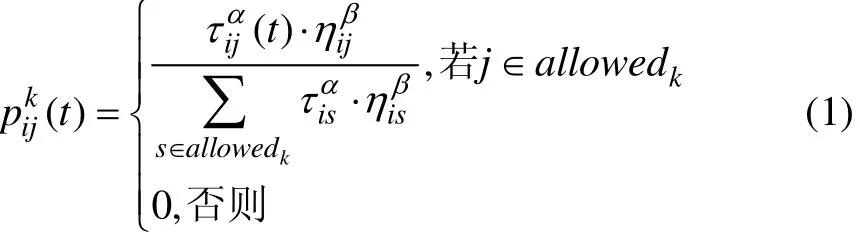
式中：allowedk={C-tabuk}，表示蚂蚁k下一步允许选择的城市；α表示信息启发式因子，表示轨迹的相对重要性，反映蚂蚁在运动过程中所积累的信息在蚂蚁运动时所起的作用，其值越大，则该蚂蚁越倾向于选择其他蚂蚁经过的路径，蚂蚁之间的协作性越强；β为期望启发式因子，表示能见度的相对重要性，反映蚂蚁在运动过程中启发信息在蚂蚁选择路径中的受重视程度，其值越大，则该状态转移概率越符合贪心规则；ηij(t )为启发函数，其表达式为：

为了避免残留信息素过多导致残留信息淹没启发信息，在每只蚂蚁走完1步或者完成对所有n个城市的遍历后，要对残留信息进行局部更新处理。由此，在t+n时刻，在城市i和j之间的路径上的信息量可按如下规则进行调整：

式中：ρ∈(0,1)表示信息素含量τil( t )随时间的推移而衰减的程度；(t)表示本次循环中城市i和j之间路径上的信息素增量，初始时刻 Δ τ(0 )=0，(t)是

ij蚂蚁k在本次循环中在城市i和城市j之间路径上留下的信息素。

所有蚂蚁走完全部城市以后，仅对最优路径上的信息素按式(3)进行更新。信息素全局更新公式为：

其中：Lb为本次循环中最优路径的长度。

根据信息素更新策略的不同，Dorigo等[1-2]给出3种不同的基本蚁群算法模型，分别称为蚁周系统(Ant-cycle system)、蚁量系统(Ant-quantity system)和蚁密系统(Ant-density system)，计算公式分别见式(4)～(6)。

在蚁周系统(Ant-cycle system)中，

式中：Q为常数，表示每只蚂蚁周游1遍留下的信息总量；Lk为蚂蚁k在本次循环中所走路径的长度；

在蚁量系统(Ant-quantity system)中，

在蚁密系统(Ant-density system)中，

蚁密和蚁量系统利用的是局部信息，即蚂蚁完成1步更新路径上的信息素，而蚁周系统用的是整体信息，即蚂蚁完成1个循环后更新所有路径上的信息素，在求解TSP中，蚁周系统的性能较好。因此，通常采用蚁周系统作为蚁群算法的基本模型。

3 传统的最优-最差蚂蚁系统

3.1 最优-最差蚂蚁系统概念

最优-最差蚂蚁系统[6]在蚁群算法的基础上进一步增强搜索过程的指导性，使得蚂蚁的搜索更集中于到当前循环为止所找出的最优路径的领域内。蚁群算法的任务就是引导问题的解向着全局最优的方向不断进化。这种引导机制建立的基础是解决方案越好，越可能在它的附近找出更优的解。因此，将搜索集中于所找出的最优解附近是合理的。算法的思想就是对最优解进行更大限度的增强，而对最差解进行削弱，使得属于最优路径的边与属于最差路径的边之间的信息素量差异进一步增大，从而使得蚂蚁的搜索更集中于最优解附近。该算法主要修改蚁群系统中的全局更新公式。当所有的蚂蚁完成1次循环后，增大对最差蚂蚁路径的信息素更新。若(i,j)为最差蚂蚁路径中的 1条边，且不是最优蚂蚁路径中的边，则该边上的信息素按下式更新：

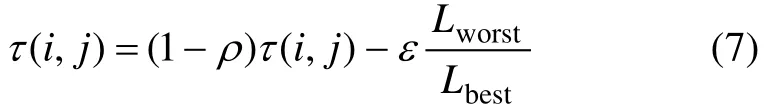
其中：ε为引入的参数；Lworst为当前循环中最差蚂蚁中路径长度；Lbest为当前循环中最优蚂蚁的路径长度；为城市i和城市j之间的信息素轨迹量。

3.2 传统最优-最差蚂蚁系统的不足

传统最优-最差蚂蚁系统对最差蚂蚁所执行的全局更新可以改善算法的性能，从而使得最优-最差蚂蚁系统的收敛速度比蚁群系统的快，但其存在一定的不足：首先，由于各路径上的初始信息素相同，蚂蚁创建的第1条路径的引导信息主要是城市间的距离信息，这样，蚂蚁在所经过的路径上所留下的信息素不一定能反映最优路径的方向，特别是群体中个体数目较少或者所计算的路径组合较多时，就更不能保证蚂蚁创建的第1条路径能引导蚁群走向全局最优解；其次，在初始阶段，最差路径中可能存在最优路径中没有搜索到较好的若干路段。若在初始阶段就对最差蚂蚁的路径信息素进行削弱，将会影响搜索的全局性，阻碍蚂蚁搜索到全局最优解。

4 基于启发式演化算法的最优-最差蚂蚁系统(IEABWAS)

为提高算法的全局搜索能力，加快最优解的收敛速度，在文献[6, 8]的基础上，针对以上传统最优-最差蚂蚁系统算法的不足，提出以下改进措施。

(1) 采用在每次循环后加入一种启发式交叉算子的方式[8]。这种方式不只是单纯地进行随机交叉，而是综合父代基因，再根据各个城市之间的连接关系的一种启发式交叉方式。将最优路径和次优路径进行交叉，通过这种交叉得到的子代有效地继承父代较好的基因，从而有利于发现最优解，加快算法的收敛速度。

(2) 在蚂蚁运行的初始阶段，不对最差蚂蚁信息素进行削弱，而是在蚂蚁运行若干代以及大致确定进化方向之后，再对最差蚂蚁的信息素进行更新，从而削弱最差路径上的信息量。

将以上2种措施相结合，对最差蚂蚁信息素实施调整，使得搜索更集中于最优解附近，并通过加入启发式演化交叉算子得到可行解，有效地继承父代优秀的基因，更进一步加强在最优解附近的搜索能力，达到最终加快收敛速度、尽快找到全局最优解的目的。

在最优-最差蚂蚁系统的基础上，对最差蚂蚁实施的信息素更新方式作适应性调整，并且在算法中加入一种启发式交叉算子。这种改进后的新算法不但加快算法的收敛速度，而且增强寻找全局最优解的能力。

4.1 IEABWAS信息素更新

在算法的初始阶段执行蚁群算法，对每次循环后的最差蚂蚁不更新信息素。当算法运行到一定代时，方向已基本确定(取最大循环代数的 1/4，此时进化方向已经大致确定)，路径图中各条边上的信息素基本与距离成正比。将最差蚂蚁按公式(7)进行信息素更新，削弱最差路径中的信息量，使得蚂蚁更倾向于选择最优路径附近的边，从而快速地搜索到最优解。

4.2 IEABWAS启发式交叉算子

在演化计算中，常见的交叉算子有部分匹配交叉算子PMX、顺序交叉算子OX、循环交叉算子CX等。这些交叉算子带有很大的随机性，不能很好地利用父个体的优良性能，最终不能提高寻优的速度。因此，本文作者采用一种启发式交叉算子。该交叉算子考虑城市之间的连接关系并很好地继承父代的优秀基因，从而提高寻优的速度，加快收敛到全局最优解[8]。交叉方式如下：

随机选择2个父代个体X=( x1, x2, …, xn)，Y=(y1,y2, …, yn)，将编码串看作一个环行回路[12]。通过启发式交叉算子产生子代child的过程为：

(1) 随机选定1个城市xi作为交叉的起点，将xi加入到子代child中。

(2) 记当前城市c为xi，分别找到X和Y中城市xi的下1个城市 xi+1和 yj+1，如果 xi+1和 yj+1均不在子代中，并且有d(xi, xi+1)≤d(yi, yi+1)，就将xi+1加入到child中，记当前城市c为xi+1，否则，将yi+1加入到child中，并记当前城市c为yi+1。

(3) 若xi+1已经在子代中，而yj+1不在子代中，则将yj+1作为当前城市并加入到子代中；若yi+1已经在子代中，而xj+1不在子代中，则将xj+1作为当前城市并加入到子代中；若xi+1和yj+1均在子代中，则比较d(xi, xi+2)和 d(yi, yi+2)。

(4) 重复执行步骤(2)，直到完整地生成子代为止。

这种交叉方式得到的子代是可行的，虽然不能保证得到的子代一定比父代优，但在很大程度上继承了父代优秀的基因，达到交叉的目地。实验表明：此交叉方式对小规模的TSP求得最优解的效果最明显，而且能显著提高收敛速度。对于大规模的TSP，此交叉算子也能很快地找到近似最优解，并且解的质量较好。该交叉方式同样适用于其他演化算法。

4.3 IEABWAS算法的实现步骤

根据以上分析，改进的基于启发式演化交叉算子的最优-最差蚂蚁系统算法的实现步骤如下。

(1) 参数初始化。令时间t=0和循环次数Nc=0，设置最大循环次数Nmax，将m只蚂蚁置于n个城市上，令每条边上的初始信息量τil(t)=const(其中，const为常数)，且初始时刻

(2) 对每只蚂蚁随机选择1个初始位置；

(3) 按式(1)计算尚未走过的城市转移概率，采用轮盘赌方式选择策略为每只蚂蚁选择下1个要转移的位置，按式(2)执行局部信息素更新；

(4) 重复步骤(2)，直到所有蚂蚁都完成1次遍历为止；

(5) 计算每只蚂蚁的路径长度并排序，分别找到最优、次优和最差蚂蚁并记录；

(6) 对最优蚂蚁按式(3)执行全局信息素更新规则，若算法运行到最大循环代数的1/4，则对最差蚂蚁按式(7)执行信息素更新规则，否则，不执行信息素更新；

(7) 将最优蚂蚁和次优蚂蚁路径执行启发式演化交叉得到另一条新路径，并对所有蚂蚁重新排序，将最差蚂蚁排除；

(8) 记录到目前为止最短的路径，若 Nc＜Nmax，则清空禁忌表继续下1轮循环，否则，输出最优路径。

表1 不同算法的实验结果对比Table 1 Comparison results of different algorithms

5 数据仿真实验

为验证改进的IEABWAS算法对全局最优解的搜索能力和收敛速度，选用国际通用的 TSP测试库TSPLIB中的Oliver30，Att48，Eil51和Eil75这4个实例，用 VC++对不同的算法进行编程实现，分别进行测试比较。

实验中设置的参数分别为：蚂蚁数目与城市数目相同，最大循环代数为3 000次，启发因子α=1，期望因子β=5，信息素挥发度ρ=0.7，最差蚂蚁更新参数ε=10，总信息量 Q=100。对各个实例分别运行 20次，测试结果如表1所示，其中ACS算法实验数据来源于文献[2]，BWAS算法实验数据来源于文献[4]。运用 IEABWAS算法，得到 Oliver30，Att48，Eil51和Eil75这4个实例的最优路径分别如图1～4所示。

从表1可以看出，IEABWAS算法无论是在解的质量上还是在求解的速度上，都明显优于传统蚁群(ACS)算法和最优-最差蚂蚁系统(BWAS)算法，表明改进算法具有更强的全局搜索最优解的能力，而且在收敛速度上也有较大的提高，算法的性能得到提高。

图1 Olive30的最优路径示意图Fig.1 Optimal path sketch map of Olive 30

图2 Att48的最优路径示意图Fig.2 Optimal path sketch map of Att48

图3 Eil51的最优路径示意图Fig.3 Optimal path sketch map of Eil51

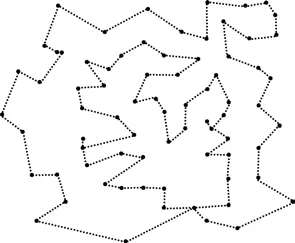
图4 Eil75的最优路径示意图Fig.4 Optimal path sketch map of Eil75

6 结论

(1) 提出一种基于启发式演化算法的最优-最差蚂蚁系统(IEABWAS)算法。与传统的最优-最差蚂蚁系统算法相比，IEABWAS算法的性能得到明显改善，并具有更强的全局搜索能力和较快的收敛速度。

(2) 算法自适应地对最差蚂蚁实施信息素调整，以削弱最差解，使搜索更集中于较优解附近，从而有效地引导了蚂蚁的路径，提高了算法的全局搜索能力。

(3) 算法在迭代过程中加入启发式演化交叉算子，将这种交叉算子得到的较优解来替代较差解，从而进一步加强了对最优解附近的搜索能力。

[1] Dorigo M, Maniezzo V, Colorni A. The ant system: Optimization by a colony of cooperating agents[J]. IEEE Transaction on Systems, Man, and Cybernetic-Part B, 1996, 26(1): 29-41.

[2] Dorigo M, Gambardella L M. Ant colonies for the traveling salesman problem[J]. BioSystems, 1997, 43(2): 73-81.

[3] Stutzle T, Hoos H. Max-min ant systems[J]. Future Generation Computer Systems, 2000, 16(8): 889-914.

[4] 李士勇, 陈永强, 李研. 蚁群算法及其应用[M]. 哈尔滨: 哈尔滨工业大学出版社, 2004.LI Shi-yong, CHEN Yong-qiang, LI Yan. Ant colony algorithm and its application[M]. Harbin: Harbin Industry University Press,2004.

[5] 吴启迪. 智能蚁群算法及应用[M]. 上海: 上海科技教育出版社, 2004.WU Qi-di. Intelligent ant colony algorithms with applications[M]. Shanghai: Shanghai Technical Education Press, 2004.

[6] 段海滨. 蚁群算法原理及应用[M]. 北京: 北京科学出版社,2005.DUAN Hai-bin. Ant colony algorithms principle and applications[M]. Beijing: Beijing Science Press, 2005.

[7] 潘正君, 康立山, 陈毓屏. 演化计算[M]. 北京: 清华大学出版社, 1998.PAN Zheng-jun, KANG Li-shan, CHEN Yu-ping. Evolutionary computation[M]. Beijing: Tsinghua University Press, 1998.

[8] 刘海, 郝志峰. 改进遗传交叉算子求解 TSP问题[J]. 华南理工大学学报, 2002, 30(12): 71-73.LIU Hai, HAO Zhi-feng. Improving genetic cross operator to solve TSP problem[J]. Journal of Huanan University of Science and Technology, 2002, 30(12): 71-73.

[9] 刘立东, 蔡淮. 融入遗传算法的混和蚁群算法[J]. 计算机工程与设计, 2008, 29(5): 1248-1250.LIU Li-dong, CAI Huai. Novel hybrid algorithm of combination of genetic algorithm and ant colony algorithm[J]. Computer Engineering and Design, 2008, 29(5): 1248-1250.

[10] 陈烨. 带杂交算子的蚁群算法[J]. 计算机工程, 2001, 27(12):74-76.CHEN Ye. An ant colony algorithm with crossover operator[J].Computer Engineering, 2001, 27(12): 74-76.

[11] 吴庆洪, 张纪会, 徐心和. 具有变异特征的蚁群算法[J]. 计算机研究与发展, 1999, 36(10): 1240-1245.WU Qing-hong, ZHANG Ji-hui, XU Xin-he. An ant colony algorithm with mutate on features[J]. Journal of Computer Research and Development, 1999, 36(10): 1240-1245.

[12] 龚本灿, 李腊元. 基于信息素适量更新与变异的高效蚁群算法[J]. 计算机工程与应用, 2008, 44(1): 45-48.GONG Ben-can, LI La-yuan. Efficient ant colony algorithm based on right pheromone updating and mutation[J]. Computer Engineering and Technology, 2008, 44(1): 45-48.

[13] 孙力娟, 王良俊, 王汝传. 改进的蚁群算法及其在 TSP中的应用研究[J]. 通信学报, 2004, 25(10): 111-116.SUN Li-juan, WANG Liang-jun, WANG Ru-chuan. Research of using an improved ant colony algorithm to solve TSP[J]. Journal of China Institute of Communication, 2004, 25(10): 111-116.

[14] 谭冠政, 李文斌. 基于蚁群算法的智能人工腿最优 PID 控制器设计[J]. 中南大学学报: 自然科学版, 2004, 35(1): 91-96.TAN Guan-zheng, LI Wen-bin. Design of ant algorithm based optimal PID controller and it s application to intelligent artificial leg[J]. Journal of Central South University: Science and Technology, 2004, 35(1): 91-96.

[15] TAN Guan-zheng, DOU Hong-quan. ACS algorithm-based adaptive fuzzy PID controller and its application to CIP-I intelligent leg[J]. Journal of Central South University of Technology, 2007, 14(4): 584-588.