1—AGO灰关联分析模型
2010-05-29杨建华
杨建华
(武汉工程大学理学院,智能机器人湖北省重点实验室,湖北 武汉 430074)
0 引 言
灰色系统[1]理论及其方法在社会、经济、工业、农业、生态、工程等各方面都得到了很好地应用[2-5],其中关联分析[6-7]在对动态过程发展态势进行量化比较分析起了十分重要的作用.在[8]中对灰关联分析模型加以改进,提出了指数型灰关联分析模型,该模型克服了一般灰关联分析模型不考虑数据波动方向对关联度的影响的不足,但其使用了指数变换,不能保证线性性的成立.本文利用灰色系统常用的方法1—AGO,对一般灰关联分析模型进行改进,提出了下面的模型.
1 1—AGO灰关联分析模型
设有m+1个数列xi=(xi(1),xi(2),…,xi(n)),(i=0,1,2,…,m),将它们初值化处理仍记为xi=(xi(1),xi(2),…,xi(n)),(i=0,1,2,…,m),再将xi=(xi(1),xi(2),…,xi(n)),(i=0,1,2,…,m)作AGO处理得原数列的AGO数列AGO(xi)=(AGO(xi(1)),AGO(xi(2)),…,AGO(xi(n))),(i=0,1,2,…,m),其中AGO(xi(k))=xi(1)+xi(2)+…+xi(k),(k=1,2,…,n).定义xi(i=1,2,…,m)对x0在k时刻的1—AGO型关联系数为
AGOξi(k)=AGOγ(x0(k),xi(k))=

[|AGO(x0(k))-AGO(xi(k))|+
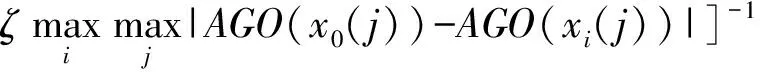
其中分辨系数ζ一般在0与1之间选取.xi(i=1,2,…,m)对x0的1—AGO型关联度为
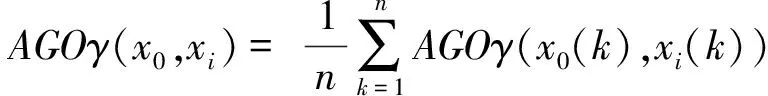
(i=1,2,…,m)
2 模型的合理性
记
X={xi|i=0,1,2,…,m}
Δoi(j)=|AGO(x0(j))-AGO(xi(j))|
I={1,2,…,m},J={1,2,…,n}

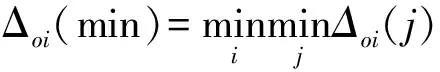
Δ={Δoi(j)|i∈I,j∈J}
ΔGR={Δ,ζ,Δoi(max),Δoi(min)}
则AGOγ(x0,xi)满足灰关联公理[7]:
a. 规范性
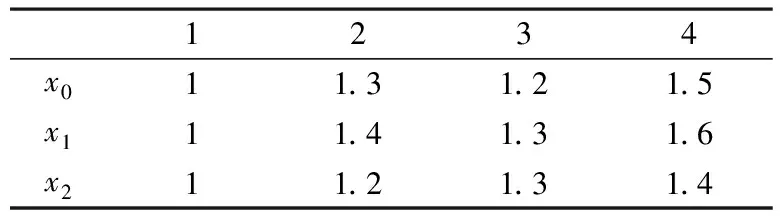
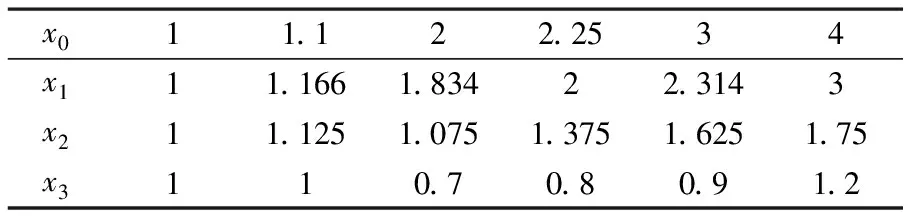
0 AGOγ(x0,xi)=1⟺x0=xi AGOγ(x0,xi)=0⟺x0,xi∈Φ b. 偶对对称性 AGOγ(x,y)=AGOγ(x,y) iffX={x,y} c. 整体性 xi,x∈X={xi|i=1,2,…,m;m>3} d. 接近性 差异信息Δoi(j)越小,则AGOγ(x0(j),xi(j))越大. 即 Δoi(j)↓⟹AGOγ(x0(j),xi(j))↑ 所以AGOγ(x0,xi)为灰关联映射. AGO关联系数、关联度具有线性性. 定理1设yi=xi+b,即yi(k)=xi(k)+b(k=1,2,…,m)其中b为常数,记xi,yi(i=1,2,…,m)对x0,y0在k时刻的AGO型关联系数分别为AGOγ(x0(k),xi(k))和AGOγ(y0(k),yi(k)),xi,yj(i=1,2,…,m)对x0,y0的AGO型关联度分别为AGOγ(x0,xi)和AGOγ(y0,yi),则 AGOγ(x0(k),xi(k))=AGOγ(y0(k),yi(k)),AGOγ(x0,xi)=AGOγ(y0,yi). 证 AGOγ(y0(k),yi(k))= [|AGO(y0(k))-AGO(yi(k))|+ [|AGO(x0(k)+b)-AGO(xi(k)+b)|+ [|AGO(x0(k))-AGO(xi(k))|+ AGOγ(x0(k),xi(k)) (i=1,2,…,m) 定理2设yi=axi,即yi(k)=axi(k)(k=1,2,…,n;i=0,1,2,…,m),其中a为常数,xi,yi(i=1,2,…,m)对x0,y0在k时刻的AGO型关联系数分别为AGOγ(x0(k),xi(k))和AGOγ(y0(k),yi(k))对x0,y0的AGO型关联度分别为AGOγ(x0,xi)和AGOγ(y0,yi),则 AGOγ(x0(k),xi(k))=AGOγ(y0(k),yi(k)), AGOγ(x0,xi)=AGOγ(y0,yi). 证 AGOγ(y0(k),yi(k))= [|AGO(y0(k))-AGO(yi(k))|+ [|AGO(ax0(k))-AGO(axi(k))|+ [|AGO(x0(k))-AGO(xi(k))|+ AGOγ(x0(k),xi(k)) (i=1,2,…,m) 例1 设有3组数列如表1[8]. 表1 原始数据表A 取ζ=0.5计算得xi(i=1,2)对x0在k时刻的关联系数分别为 ξ1(1)=1,ξ1(2)=0.333, ξ1(3)=0.333,ξ1(4)=0.333; ξ2(1)=1,ξ2(2)=0.333, ξ2(3)=0.333,ξ2(4)=0.333. xi(i=1,2)对x0的关联度分别为 r1=0.5,r2=0.5 取ζ=0.5计算得xi(i=1,2)对x0在k时刻的1—AGO型关联系数为 AGOξ1(1)=1,AGOξ1(2)=0.6, AGOξ1(3)=0.429,AGOξ1(4)=0.333; AGOξ2(1)=1,AGOξ2(2)=0.6,AGO ξ2(3)=1,AGOξ2(4)=0.6. xi(i=1,2)对x0的指数型关联度为 AGOγ(x0,x1)=0.591,AGOγ(x0,x2)=0.8;AGOγ(x0,x1) 例2 设有已初值化的4个数列如表2[6]. 表2 原始数据表B 取ζ=0.5计算得xi(i=1,2,3)对x0在k时刻的关联系数分别为 ξ1(1)=1,ξ1(2)=0.955,ξ1(3)=0.894, ξ1(4)=0.848,ξ1(5)=0.679,ξ1(6)=0.583; ξ2(1)=1,ξ2(2)=0.982,ξ2(3)=0.602, ξ2(4)=0.645,ξ2(5)=0.797,ξ2(6)=0.383; ξ3(1)=1,ξ3(2)=0.933,ξ3(3)=0.52, ξ3(4)=0.49,ξ3(5)=0.4,ξ3(6)=0.34; xi(i=1,2,3)对x0的关联度分别为 r1=0.827,r2=0.73,r3=0.613;r1>r2>r3. 取ζ=0.5计算得x1(i=1,2,3)对x0在k时刻的AGO型关联系数为 AGOξ1(1)=1,AGOξ1(2)=0.983, AGOξ1(3)=0.975,AGOξ1(4)=0.963, AGOξ1(5)=0.789,AGOξ1(6)=0.656; AGOξ2(1)=1,AGOξ2(2)=0.994, AGOξ2(3)=0.812,AGOξ2(4)=0.711, AGOξ2(5)=0.552,AGOξ2(6)=0.418; AGOξ3(1)=1,AGOξ3(2)=0.975, AGOξ3(3)=0.735,AGOξ3(4)=0.594, AGOξ3(5)=0.438,AGOξ3(6)=0.333; xi(i=1,2,3)对x0的AGO关联度分别为 AGOγ(x0,x1)=0.894,AGOγ(x0,x2)=0.747, AGOγ(x0,x3)=0.679;AGOγ(x0,x1)>AGOγ(x0,x2)>AGOγ(x0,x3) 1—AGO型关联分析模型对动态过程发展态势进行量化比较分析时较一般关联分析模型更精确、更科学、更合理,具有更高的分辨率,克服了一般关联分析模型不考虑数据波动方向对关联度的影响的不足,因此1—AGO型关联分析模型具有更广泛的应用性. 参考文献: [1]Deng Ju-long.The Control Problems of Grey Systems[J].Systems & Control Letters,1982(5):288-294. [2]邓聚龙.灰色系统(社会·经济)[M].北京:国防工业出版社,1985. [3]邓聚龙.灰色系统与农业区划[J].农业资源与区划,1984(4):1-12. [4]邓聚龙.棉蚜虫生物防治灰色模型[J].大自然探索,1984(3):44-49. [5]杨建华,高永东.灰关联度在边坡稳定性分析中的应用[J].武汉化工学院学报,1999,21(2):49-51. [6]邓聚龙.灰色系统基本方法[M].武汉:华中理工大学出版社,1987:17-28. [7]邓聚龙.灰理论基础[M].武汉:华中科技大学出版社,2002:135-150. [8]杨建华.指数型灰关联分析模型[J].武汉工程大学学报,2010,32(5):108-110.3 线性性
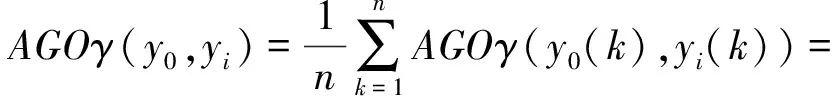

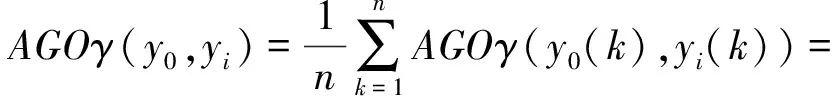

4 例 题
5 结 语
