基于小波分析的电磁干扰测量技术研究

刘 胜 张兰勇 张利军

(哈尔滨工程大学自动化学院 哈尔滨 150001)

1 引言

随着现代社会中电子设备的应用越来越广泛，各种电磁辐射已经严重影响了人们的工作和生活。所以针对设备产生的电磁辐射进行准确测量是目前急需进行的一项工作。由于受到广播电台，移动通讯，电离层辐射等各种电磁干扰的影响，对设备进行电磁干扰测量通常包含了严重的背景噪声。目前的电磁干扰测量一般需要在屏蔽室或者开阔场进行，但是屏蔽室造价昂贵并且需要很大的空间，并且受限于待测物的大小，尤其当设备已经固定在现场后，不可能进入屏蔽室。而开阔场测量为了避免无线通讯，电台通讯以及移动通讯等的影响则远离市区而引起交通不便。为了解决这个问题，Shinozuka教授提出了在市区内进行电磁兼容测量并消除环境干扰的方法[1]。此方法利用传统EMI测量接收机建立双通道在频域内测量。但是由于测量接收机在整个频率范围内进行步进扫描，所以如果频率范围需要很宽并且需要精确度很高的时候会花费大量时间。此外，此方法的应用在Parhami一篇文章中也有详细的阐述[2]。为了加快测量速度，用于实时 EMI(TDEMI)测量的新方法也被提出[3]。此方法在时域里测量辐射发射并计算其频谱。文献[3]结合了TDEMI测量节省时间的优点，提出了在时域测量受试设备辐射信号并去除环境干扰的算法。但此方法不能测量瞬时突变信号。Braun等教授提出了在时域电磁干扰的测量方法[4]，提高了电磁干扰测量精度，但是只能处理准峰值信号。Frech教授等则提出了一种新的针对电磁信号的数字信号快速处理技术[5]，可以在露天场地进行电磁辐射测量，但是处理精度较低。本文利用小波分析的方法对信号分频并设定滤波阈值对环境噪声进行有效的滤波，从而达到精确测量受试设备辐射信号，既不必在昂贵的屏蔽室测量也不必去偏远的郊区。系统中由两个双锥型极性对数天线接收辐射信号。一个天线用来测量受试设备的干扰信号与环境噪声，第2个只接收环境噪声来作为参考，测量环境噪声的天线要距离受试设备10 m。信号经过A/D转换器转化为数字信号。获得的信号在电脑上进行离散化和滤除噪声。由于被两个天线同时测得的环境噪声都是相关的，小波多级分解可以识别两通道噪声的相关性并且可以随环境干扰变化而调整小波系数。这个设计特别适用于滤除非平稳信号中的噪声信号。

2 小波分析

利用傅里叶变换对非平稳信号的线性时频进行分析有很大局限性，因为不能变化分辨率。由于小波分析具有良好的时频局部性，它为非平稳信号处理提供了强有力的工具。通过小波变换对非平稳信号的不同频率成分进行设置不同分辨率，为信号的滤波、信噪分离和弱信号特征提取提供了有效的途径。

2.1 小波变换

小波变化如下：

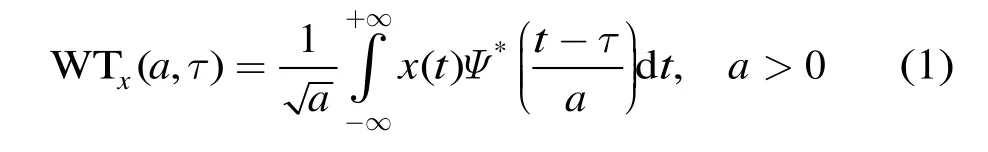
Ψ(t)为基本小波函数，a为作用尺度。

通过调节a，可以使信号在低频时时间分辨率较低，高频时时间分辨率较高，这样可以对混杂信号进行精确的滤波处理[6]。

由于Morlet小波可以实时处理并且运算速度很快，所以选用Morlet小波变换。

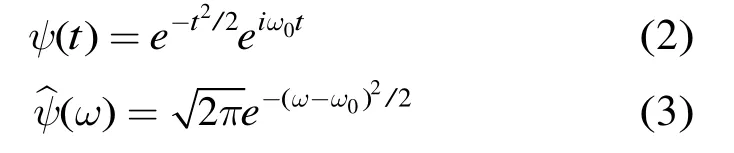
将小波函数离散化，表示为

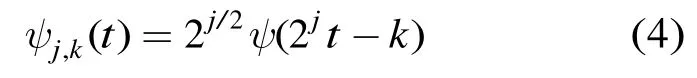
进而得到离散小波变换：

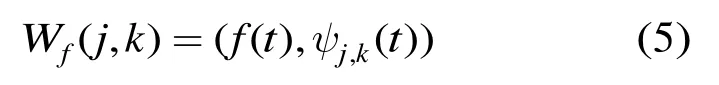
2.2 滤波阈值函数的构造

小波阈值滤波的原理是把信号的能量在小波域集中在一些大的小波系数中，而环境噪声的能量却分布于整个小波域内。经过小波分解，信号的小波系数幅值要大于干扰信号的系数幅值[7]。然后保留大尺度低分辨率下的全部小波系数，而对各尺度高分辨率下的小波系数，设定一个阈值对信号进行滤波，处理后利用逆小波重构恢复信号。所以滤波的关键问题在于阈值的确定。

目前通用的阈值滤波方法包括软阈值滤波和硬阈值滤波[8]。硬阈值法误差较小但估计的信号会产生附加振荡，而软阈值则使信号整体连续性好但偏差较大[9]。结合软阈值法和硬阈值法构造一个阈值函数，解决存在的问题。

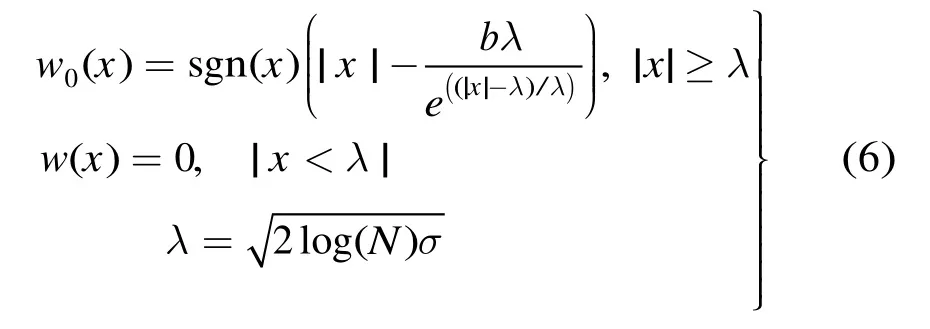
式(6)在小波域内连续并在|x|≥λ时有高阶导，同时不存在参数选择问题。当x＞0时，式(6)变为

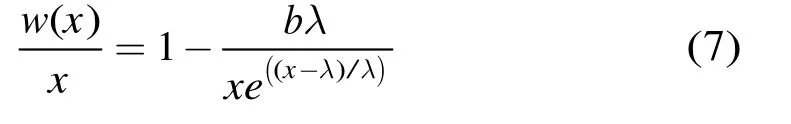
而在x＜0时

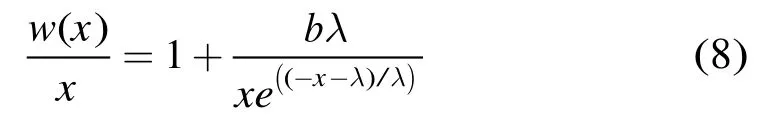
针对非平稳信号包含尖峰或突变部分的特点，传统傅里叶变换不能给出信号在某个时间点上的信号变化情况，使得信号在时间轴上的任何一个突变都会影响信号的整个谱图。而小波分析由于同时在时频中对信号进行分析，并且在低频时时间分辨率较低，高频时时间分辨率较高。利用这种自动变焦的功能，能有效区分非平稳信号中的突变部分和噪声，进而利用上面介绍的阈值函数滤波方法消噪。在 MATLAB里对基于傅里叶分析和小波分析的滤波方法进行比较。

由图 1(c)可以看出，用小波阈值函数进行非平稳信号的消噪可以很好的保存有用信号中的尖峰和突变。由图1(b)可以看出，利用傅里叶分析进行滤波时，由于信号集中在低频部分，噪声分布在高频部分，所以不能将有用信号的高频突变部分和噪声引起的高频干扰加以区分，所以未能精确重构信号。假若低通滤波器太窄时，则在滤波后，信号中仍会存在大量噪声，而弱低通滤波器太宽，则会滤除一部分有用信号。

3 基于小波变换的EMI测量系统

3.1 系统原理及信号分解

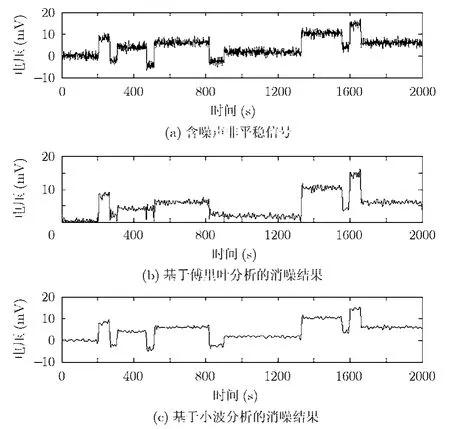
图1 非平稳信号的傅里叶分析与小波分析滤波效果比较图

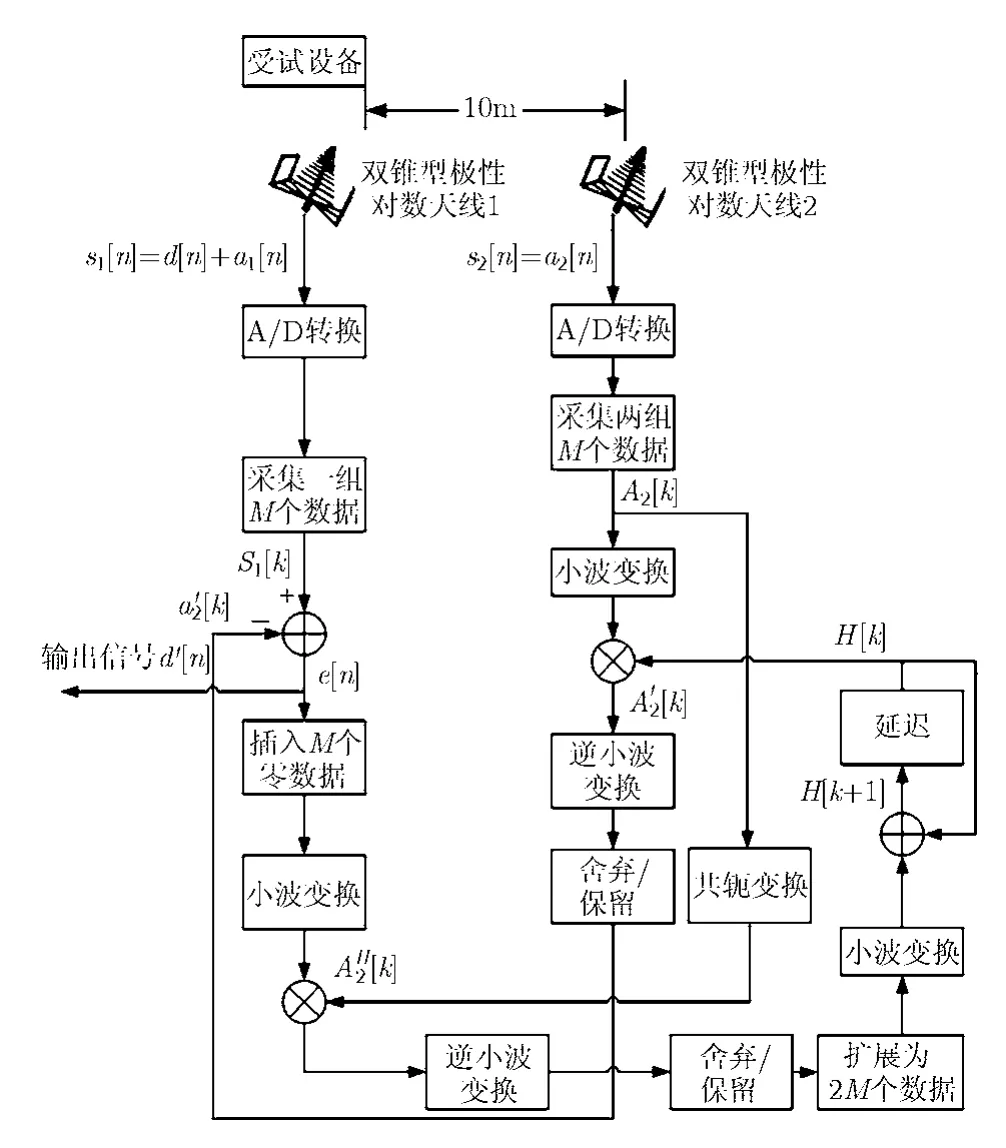
图2 基于小波变换的电磁干扰测试原理框图

系统原理框图如图2所示。天线1接受的信号s1[n]包含受试设备辐射的信号d[n]和环境干扰a1[n]。天线2与受试设备隔离仅测量环境干扰信号a2[n]。为保证天线2接受信号不受受试设备辐射影响，应该距离受试设备10 m以上。输出信号e[n]作为反馈输入到滤波器算法来调整自适应滤波器系数，这样可以得到并滤除环境干扰信号a2[n]。既然e[n]是经过消除环境干扰后的输出信号， 理论上应该只包括受试设备的信号d[n]，由于重构存在误差，所以记为d'[n]。

利用小波变换对经过 A/D转换后的离散信号进行分解如图3所示。

由信号频率的组成部分和小波分解下各频率分布可知，高频信号定位于d1层，，左上图是放大后的d1层信号图。而d4层包含了中频层的信号。在a3与a4中间出现了不连续的点，因为中频信号是由这两层共同表达的。d4层的信息有一部分被d3层减去了。所以要用a1到a3层的信息来估计中频层的信号。最后低频信号可以在a5层看出来。

如果将信号最高频率看作 1，则各层小波分解便是带通滤波器，各层具体所占频带为

所以通过小波分解可以对各个频段上的信号进行分析和处理。

3.2 阈值滤波处理

大量可应用于自适应滤波器的算法在文献[10]中有详细的介绍。本文采用小波阈值函数滤波处理信号。取样信号s1[n]包含受试设备的信号和掺入的干扰信号以及单纯的环境干扰信号a2[n]。非平稳信号一般含有突变信号，消噪的关键就是有效识别信号突变点的位置。3.1节已经对小波做多尺度分解，由于小波分解对信号突变点能作出符号一致的、且位置整齐的对应表现，同时干扰信号的分解在较细尺度层上是均匀稠密且是相关性很差的，因此，将相邻两个细尺度上的小波变换对应相乘，就能进一步增强信号在突变点处的表现并压低干扰信号。将突出表现全部放大并归一化，形成一种空间屏蔽滤波器，将屏蔽滤波器与最细层小波变换再相乘的结果，作为最细尺度层上的新的小波变换。

两路输入信号的离散信号输入到阈值函数滤波器中， 阈值由阈值函数式(6)确定。对信号增加一个平移因子h，对信号s[n]在时域平移算法为。把平移后的信号的小波系数与同频率的阈值做比较，低于阈值则为噪声滤除。Morlet小波为正交小波，具有平移不变性，所以平移后的信号进行去噪不改变原信号。

对信号做n次循环平移，小波去噪如下式所示：

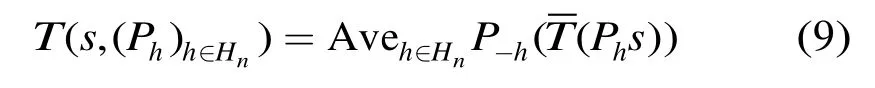
表示反向平移，Ave表示平均。

3.3 信号重构

滤波后信号的重构过程是分解的逆过程，首先计算最高层的小波系数，利用迭代式就可以重构出信号[11]。在此不再赘述。

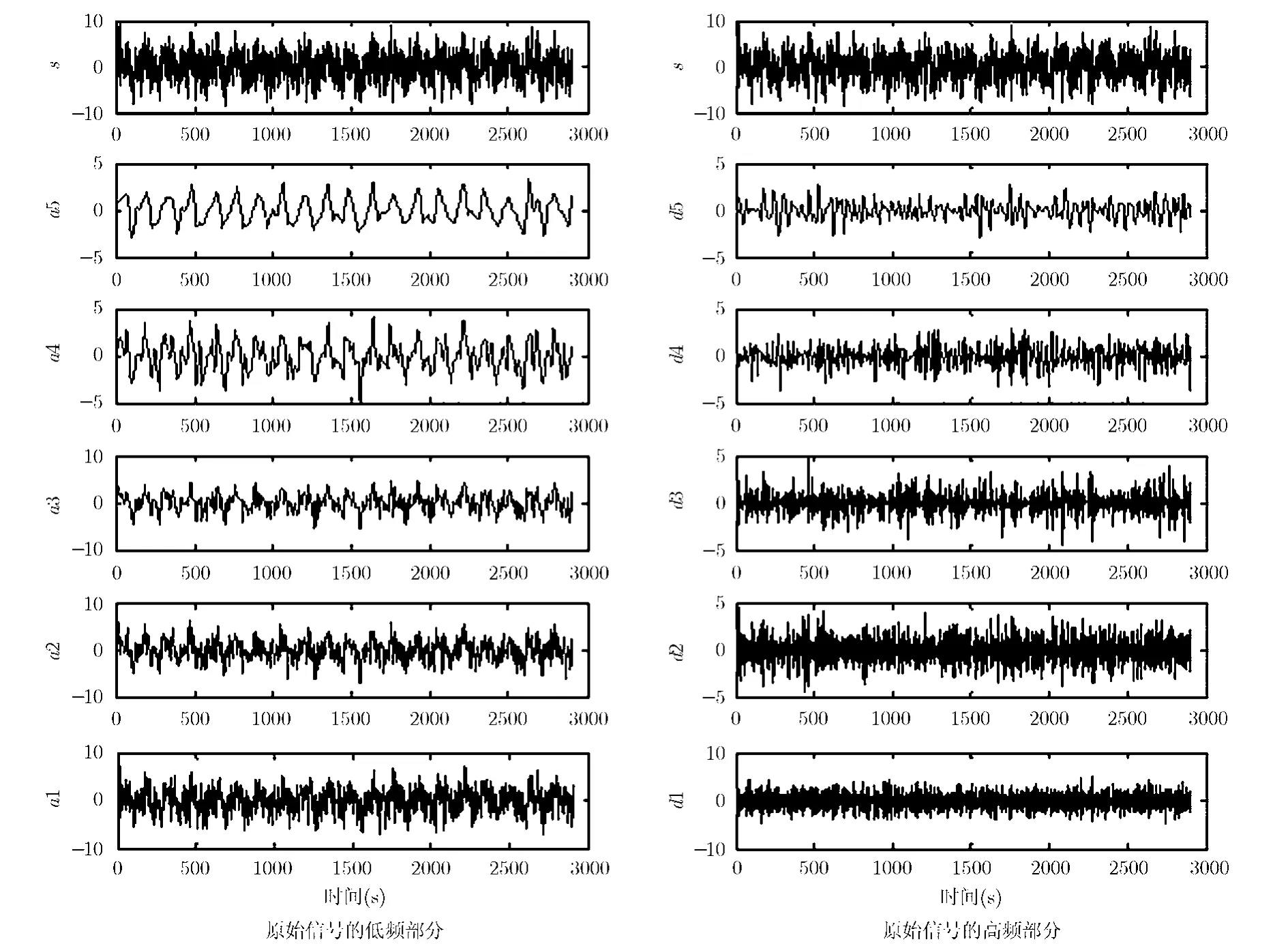
图3 测量信号的高低频分解

4 测量结果分析

4.1 仿真测量对比

以开关电源为例，环境噪声滤除方法经过了几次仿真测量试验的检验。图4表示系统利用小波分析的方法滤除环境干扰后得到的开关电源的实际电磁干扰信号频谱。

为了证明小波消噪的滤波效果，图5给出了测得的滤波前辐射信号频谱与滤波后辐射信号的频谱图。其中虚线表示抑制干扰信号后的频谱，实线表示天线1接受信号的频谱。由图4与图5对比可以看出，在调频段(FM)，移动通讯频段(GSM)，100 kHz～200 MHz之间的以及400～500 MHz线性谱都被成功滤除，大约衰减20～30 dB。而固定信号大约衰减40 dB。此外，此方法法还使210～230 MHz，地面无线电频段(575～590 MHz)以及680～760 MHz频段衰减了 10 dB。系统在成功滤除了中频，调频以及手机通讯频带的杂波的同时，受试设备的辐射信号频谱得到了保存。由于两路传播，可以把天线2与天线 1之间的有用信号与环境噪声的相关性降低到最小。进一步提高滤波效果的一种方法就是对于每一类环境噪声频率设置单独阈值进行滤除。

4.2 实验测量结果对比

为了证明本文提出方法的工程应用价值，利用本文建立的系统对某型设备在实验室中进行了实际电磁干扰测量，下面为测量结果对比。

由图6与图7对比可以看出，经过小波分析阈值滤波后的电磁辐射去除了大部分的环境电磁干扰，比如30-60 MHz的实验室电脑辐射信号，60-100 MHz的电子仪器辐射信号以及100 MHz-180 MHz的广播电视信号都被成功滤除，并且保留了设备的辐射信号。

5 结论

基于小波分析的阈值函数滤波的 EMI测量系统完美地消除了环境噪声。系统成功在很宽的频率范围内滤除或者衰减了干扰信号，尤其在调频广播信号和移动通讯频带可以衰减 30 dB。系统可连续处理其他滤波器不擅长的非平稳信号。同时，该系统由于应用了先进的数字信号处理技术，可以对受试设备进行快速而精确的电磁干扰测试。实验测试结果证明本方法可以应用于工程领域。

但应用此测量方法时小波函数的构造比较困难，虽然有参考模型，但需要对模型进行改进才能发挥最佳效果。

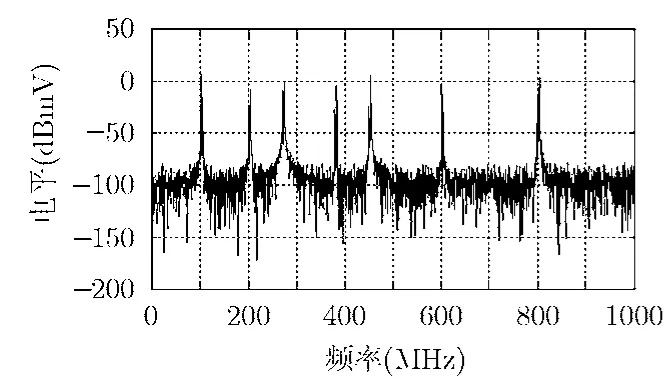
图4 开关电源实际电磁干扰信号频谱图

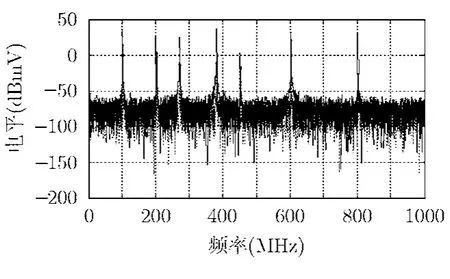
图5 含环境噪声混合信号频谱

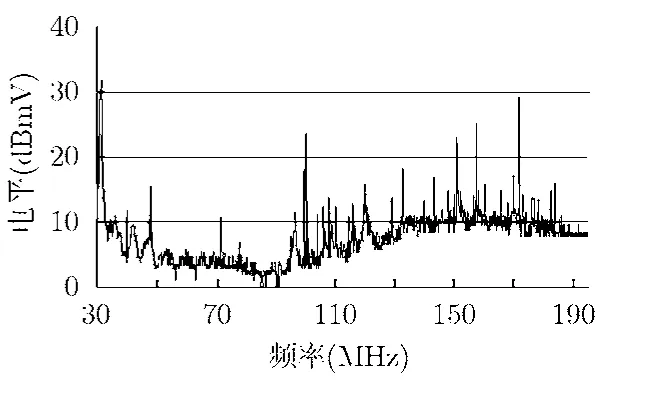
图6 未处理前测量结果

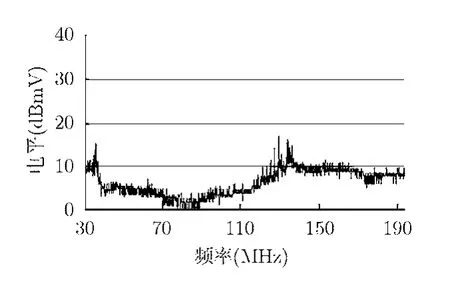
图7 处理后测量结果

[1] Shinuzuka T and Sugiura A. Reduction of ambient noise in EMI measurement [C]. IEEE International Symposium On Electromagnetic Compatibility Digest, Nagoya, Japan, 1989,September 8-10: 24-28.

[2] Parhami P, Marino M, Watkins S, and Nakauchi E.Innovative precompliance test methodology using ambient cancellation and coherence detection techniques[C]. IEEE International Symposium On Electromagnetic Compatibility,Seattle, USA, 1999: 1022-1025.

[3] Braun S, Al-Qedra M, and Russer P. A novel realtime time-domain measurement system based on field programmable gate arrays[C]. 17th International Zurich Symposium On Electromagnetic Compatibility, Singapore,2006: 501-504.

[4] Braun S, Krug F, and Russer P. A novel automatic digital quasipeak detector for a time-domain measurement system[C]. 2004 IEEE International Symposium On Electromagnetic Compatibility Digest, Santa Clara, USA,2004: 832-837.

[5] Frech A，Zakaria A, Braun S, and Russer P. Ambient noise cancelation with a time-domain EMI measurement system using adaptive filtering[C]. 2008 Asia-Pacific Sympsoium on Electromagnetic Compatibility &19th International Zurich Symposium on Electromagnetic Compatibility, Singapore,2008: 534-537.

[6] Klein A, Sauer T, Jedynak A, and Skrandies W.Conventional and wavelet coherence applied to sensory–evoked electrical brain activity [J].IEEE Transactions on Biomedical Engineering, 2006, 53(2): 266-272.

[7] Payandehjoo K. Suppression of unwanted harmonics using integrated complementary split-ring resonators in nonlinear transmission line frequency multipliers[J].IEEE Transactions on Microwave Theory and Techniques, 2008, 56(4): 931-941.

[8] Yue Zhao and Niu Wen-cheng. The application of wavelet analysis in ultrasonic sensor system characteristic signal pretreament[J].Acta Scientiarun Naturaltium Universitatis Nankaiensis, 2005, 38(2): 5-9.

[9] Zhang Hao, Blackburn T R, Phung B T, and Sen D. A novel wavelet transform technique for nn-line partial discharge measurements,IEEE Transactions on Dielectrics and Electrical Insulation. 2007, 14(1): 3-14.

[10] Huang Juan, Qian Xin, and Wang Cheng-lin. The construction of a wavelet filter and its application in environmental research[J].Journal of Nanjing University(Natural Sciences), 2007, 43(4): 389-396.

[11] Ren Shou-xin and Gao Ling. Application of a wavelet packet transform based radial basis function neural network to analyze overlapping spectral[C]. 2008 Congress on Image and Signal Processing. China, 2008: 874-878.