三电平电压空间矢量调制与 载波调制关系的研究
2010-05-26陶川辉王清灵
陶川辉 王清灵
(安徽理工大学电气与信息工程学院,安徽 淮南 232001)
1 引言
近年来,在整流和逆变等各种场合,PWM调制方式越来越多的采用多电平技术,由以前的两电平逐渐发展到三电平乃至多电平。使用三电平电路比两电平电路具有很多的突出优点。多电平电路更适合高压大功率领域。众所周知,在普通的PWM电路中,是依靠提高开关频率来实现谐波抑制。多电平电路由于电平数的增多,不必很高的开关平率,即可实现电流的正弦化,起到很好的谐波抑制,且损耗也大大降低。随着电平数的增加,电压应du/dt也相应的降低,提高了点开关元件的安全性,也使EMI强度大幅下降。关于两电平空间矢量与载波调制之间的关系,在很多文献中都有较详细的记载。然而对三电平空间矢量与载波调制的关系却较少讨论。虽然它们与载波调制的关系在本质上是一直的,都是通过零序分量联系在一起的,但是三电平空间矢量分析较复杂,不同调制比下的零序分量表达式都不相同。本文试图在理论上推导三电平空间矢量调制与载波调制的内在联系,并且用Matlab/Simulink来验证结果。
2 三电平电压空间矢量的原理
三电平电压空间矢量与两电平电压空间矢量相似,都是由NTV(nearest three vector)三个矢量来合成的。两电平电压空间矢量只有7个基本矢量。而三电平空间电压矢量却有19个基本矢量,且存在着大量的复用矢量。因此,复杂度和合成的灵活性都大大增加。如图1所示。
将ABC坐标系分为6个大扇区(sector),每个扇区又分为6个小区(region),共有36个小区。对于落入每个小区内的目标矢量,用最近的三个基本电压空间矢量来合成。以提高电压利用率为优化目标,采用7段式合成。即首发小矢量和中间矢量分别为同一基本矢量的正负小矢量。在一个采样周期中共包括3中基本矢量,4种开关状态。
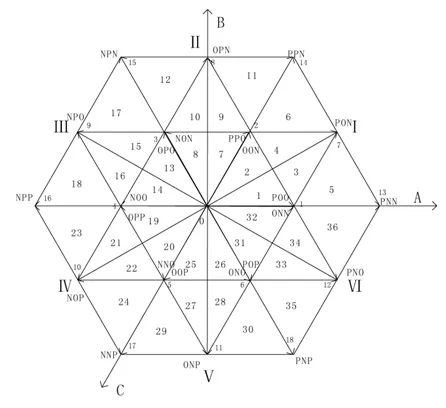
图1 三电平电压空间矢量分布图
对于落入1,2小区中的目标矢量,合成时越靠近目标矢量的基本矢量作用时间越长。例如,目标矢量落入1小区中,矢量1的作用时间大于矢量2。若落入2小区中,则矢量2作用的时间大于矢量1。依次论推其他小区中的情况。
以目标矢量落入1小区为例,分析各矢量的作用时间。根据伏秒平衡原理,得

式中,Vref为目标参考矢量。Ts为采样周期。

将(1)式按实部和虚部分别展开,可得到各矢量的作用时间。如下所示
其他区域内矢量作用时间依次论推。
3 三电平电压空间矢量调制与三角载波调制的内在联系
众所周知,对传统于两电平逆变器无中线系统,空间电压矢量调制就相当于在正弦调制波中注入适当的三次谐波,然后进行对称规则采样。但是,不能简单地把零序分量归结为三次谐波,尤其在系统的动态调整过程中,调制波的相位和幅值都在变化,有时甚至是非正弦。三电平系统中也有类似结论,分析如下:
以第24小区为例来说明,见图2。载波采用PD(phase disposition)同向层叠调制方式。

图2 第24小区三角载波PWM与SVPWM的关系
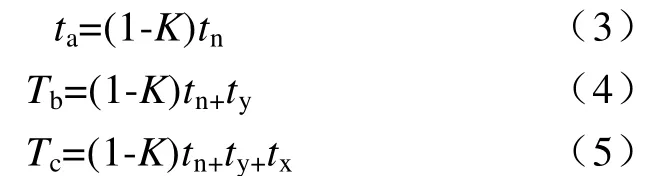
式中,tn表示负小矢量作用时间;tx表示除首发小矢量矢量外,先作用矢量的作用时间;ty表示除首发小矢量矢量外,后作用矢量的作用时间;K为小矢量作用时间分配因子。K的取值范围在0到1之间。
由图2很容易得到下面的关系式:

需要注意的是,图2中所用的量都进行了归一化。
式中,Ua*,Ub*,Uc*分别为三相的等效调制波。
根据平均状态分析法,一个采样周期内的平均值,恰好近似等于基波分量,可得出以下各式:

式中,Ua,Ub,Uc分别为三相调制波的基波分量。为三相对称波。
式(9)~(10)得

式(10)~(11)得

将式(12)~(14)带入(6)~(8),得
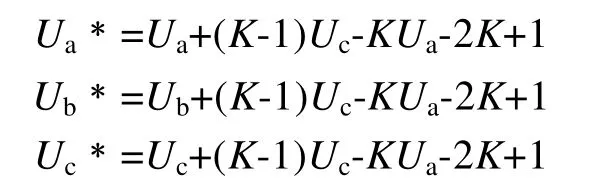
由以上各式显而易见,

同理,可对其他小区进行分析。例如分析14小区,得:

易知,Uz=(K-1)Ub-KUc-2K+1,结论与24小区相似。
以下给出第1,第2扇区内的零序分量的表达式,见表1。
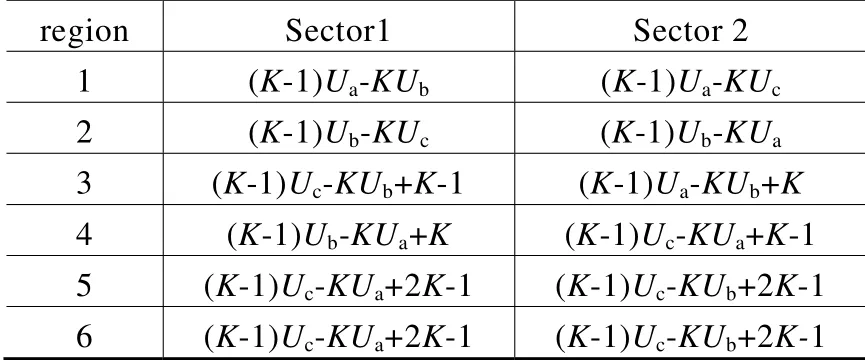
表1 第1,第2扇区内零序分量的表达式
可见,随着K取值的不同,零序电压也不同。三电平SVPWM调制与两电平SVPWM调制本质相同,都可看作是正弦波叠加零序分量,然后采用中心对称规则采样的结果。只不过两电平的零序分量是随零矢量的时间分配因子的变化而变化,三电平的零序分量是随小矢量的时间分配因子的变化而变化。
4 使用Matlab/simulink进行仿真验证
4.1 SVPWM脉冲发生器的建立
SVPWM脉冲发生器的搭建遵循下列几个步骤:
(1)目标矢量所在小区的判断。
(2)合成目标矢量所需的基本矢量的作用时间。
(3)矢量作用顺序的确定。
(4)建立开关切时间换表。
根据以上几个步骤建立的SVPWM脉冲发生器如图3所示。
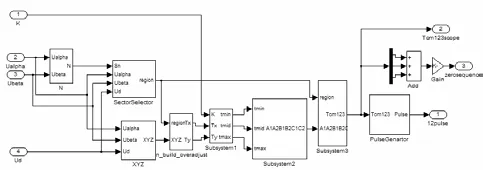
图3 三电平SVPWM脉冲发生器的Matlab模型
对模型进行封装后,如图4所示。
4.2 不同调制度下的仿真结果
图5为不同条件下的仿真结果。

图4 封装后的SVPWM脉冲发生器模型
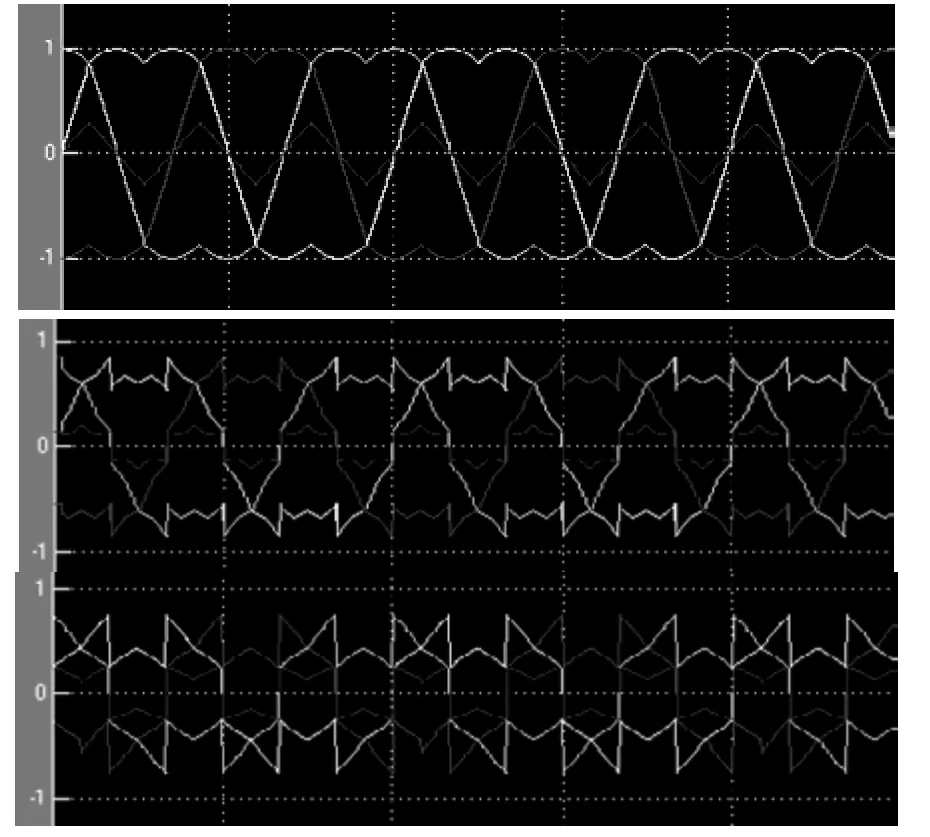
图5 从上至下分别为m=1,m=0.7,m=0.5。k=0.5 时的等效调制波形及零序电压波形(注:m为调制度,k为分配因子)
对于三电平电路,由于拓扑的原因存在中点点位的波动。可以通过控制小矢量的分配因子K来实现中点点位的控制。

图6 从上至下分别为m=1,m=0.7,m=0.5, k=0时的等效调制波形及零序电压波形(注:m为调制度,k为分配因子)

图7 从上至下分别为m=1,m=0.7,m=0.5, k=1时的等效调制波形及零序电压波形(注:m为调制度,k为分配因子)
5 结论
三电平电压空间矢量的生成可通过在正弦调制波中注入适当的零序电压,并采用对称规则采样得到。通过控制分配因子K来对零序电压进行控制,以达到不同的优化目标。
[1] 林渭勋.现代电力电子技术[M].第1版.北京:机械工业出版社,2007.
[2] 李永东,肖曦,高跃.大容量多电平变换器[M].第1版.北京: 科学出版社,2005.
[3] 肖鹏,宋文祥,陈国成.三电平空间矢量调制与三角波调制内在联系的研究[J].电气传动自动化,2007,29(3): 7-10.
[4] 蔡凯,程善美.三电平SVPWM方案的实现[J].电气传动自动化,2008,30(4):5-8.
