曹妃甸水流挟沙力计算方法分析

黄惠明，王义刚，孟 超

（河海大学海岸灾害及防护教育部重点实验室，南京 210098）

曹妃甸地处唐山南部的渤海湾西岸，位于天津港和京唐港之间。曹妃甸具有优良的建港条件和广阔的滩涂，已成为渤海湾大型深水港口和邻港工业开发区开发建设的黄金海岸［1］。根据曹妃甸工业区2004～2020年规划的要求，曹妃甸浅滩将填海造陆310 km2，同时还将利用曹妃甸天然港址的优势，建设数个10万t级以上码头［2-3］。如此大规模的海域开发利用，使曹妃甸周边海域的水沙环境变迁、海床岸线演变等研究显得尤为重要。为深入研究曹妃甸工程实施后周边海域的水沙环境及海床等的演变情况，掌握该海域水流的挟沙能力也显得至关重要。

水流挟沙能力通常是指在一定的水流泥沙及边界条件下，单位水体能够挟带和输送的泥沙数量，包括推移质和悬移质在内的全部数量，但习惯上称为水流挟带悬移质中床沙质的能力［4］。目前，关于河口海岸区域的水流挟沙能力的主要研究成果还是基于恒定流理论得到的，虽然刘家驹、窦国仁等就波浪及潮流共同作用下的水流挟沙能力进行了卓有成效的研究，但由于河口海岸区域水流挟沙、输沙的复杂性，现阶段关于河口海岸水域的水流挟沙力的研究仍相对薄弱，因此工程中通常利用水域实测资料，结合常用水流挟沙力公式进行拟合，以掌握当地海域水流挟沙能力随水流等要素变化的特征。

为了准确地把握曹妃甸附近海域水流挟沙力随水动力条件变化的情况，根据曹妃甸水域的实测水文泥沙资料，选取国内典型和常见的挟沙力计算公式进行拟合计算，通过比较分析，选取能较为准确地反映曹妃甸水域挟沙能力的计算方法。

1 常用挟沙力公式

河口海岸区域水流挟沙能力的研究成果众多，实际工程中，应用较为广泛的主要包含2大类：基于潮流作用下的挟沙能力以及明渠水流挟沙能力公式的移植［4］。通过分析各个具代表性的挟沙力公式的结构可知，众多公式包含了反映水流动力紊动强度的弗劳德数项U2/gh或反映紊动作用与重力作用相互对比关系的相对重力作用项ω/U。这类公式通常是基于半经验半理论得到的，具有结构简单、应用方便的特点，且具有有限个数的未知参量，可通过实测资料进行拟合分析，因此在实际工程中应用非常广泛。这类型的常用公式如下。

刘家驹［5］通过分析认为近岸海区浅水体含沙量与风吹流、波浪和潮流等密切相关，同时也与泥沙沉速和水深等因素有关，最后经过因次分析，得到了以弗劳德数为主体的挟沙力公式，具体形式为

式中：U为流速，可化为潮流与波浪的分流速、风吹流流速等；k，m为待定系数和指数；h为水深；g为重力加速度。

武汉水利水电学院在收集大量实测资料进行整理后，基于悬移质具有制紊作用的观点，得到悬移质中属于床沙质部分的临界含沙量和代表水流条件与床面组成条件综合因子U3/ghω之间关系的水流挟沙能力公式［6］，具体形式为

式中：ω为泥沙沉速，其余各变量同式（1）。

浙江水利科学研究所［7］基于钱塘江河口的实测资料，按照半潮平均分析得到半潮含沙量关系式，具体形式为

式中：S为含沙量，其余各变量同式（1）。

我国《海港水文规范》（JTJ213-98）推荐使用刘家驹以天津港和连云港海区的实测资料为依据而建立的半经验半理论水流挟沙力计算公式，当仅考虑潮流作用时，具体形式为

式中：γs为泥沙颗粒容重，其余各变量同式（1）。

窦国仁［8］依据能量迭加原理所得到的潮流波浪作用下的挟沙力公式，当仅考虑潮流作用时，具体形式为

式中：n为底床糙率，其余各变量同式（1）。

张燕菁［9］认为影响输沙能力的主要因素为水流动力及絮凝作用，并通过量纲分析的方法得到的黄河口水流挟沙能力公式的形式之一为

式中：各变量同式（1）。

2 不同挟沙力计算方法比较

上述各个类型的水流挟沙力公式虽然均在实际应用中取得了一定的成功，但在曹妃甸区域的应用还需要进一步的检验。为此，利用2006年夏季曹妃甸附近水域2个潮周期范围内的实测水文泥沙资料就上述各个公式在该区域应用的效果进行比较和分析。

表1给出了上述相关公式利用半潮平均水文泥沙资料进行拟合之后所得到的相应公式。

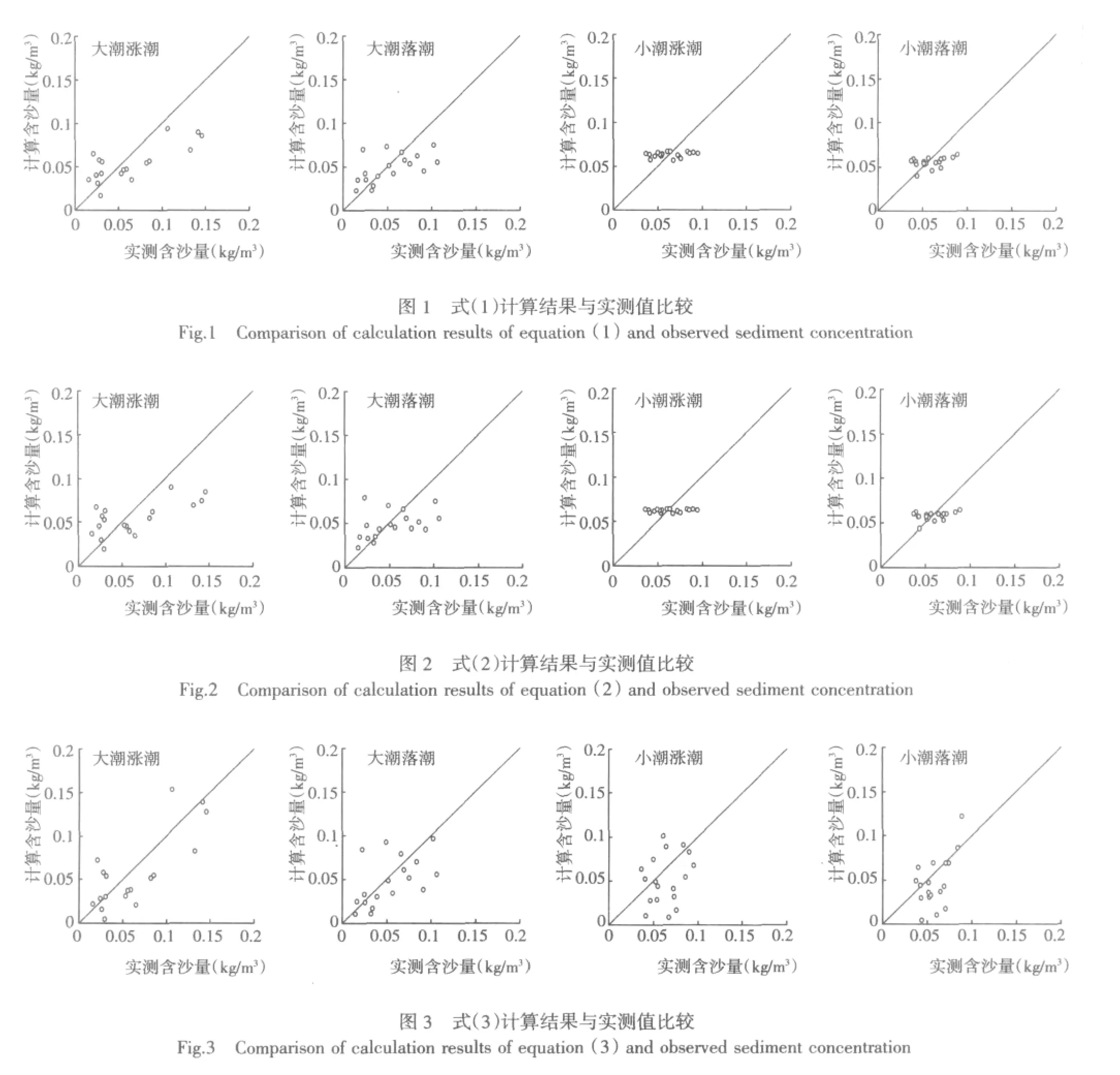
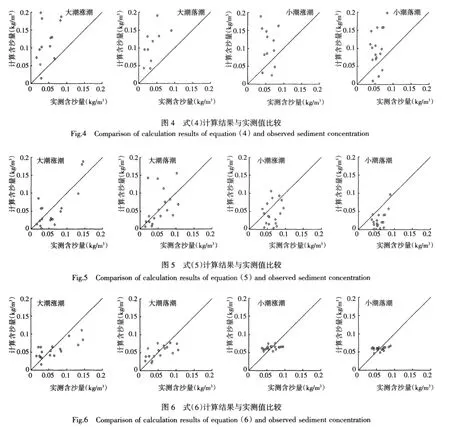
为进一步比较分析各个计算公式在曹妃甸海域的适用性和精度，将上述公式拟合结果以及刘家驹和窦国仁公式计算结果与实测资料进行了比较（图1～图6）。

集中系数表征了2个变量之间的算术平均值，可以用来衡量2个变量总体趋于45°线的程度，当集中系数越接近1时，说明二者比值趋于1:1，而偏离系数则表征了2个变量之间的平均偏离值，可以用来衡量2个变量总体偏离45°线的程度，当偏离系数越小，则表明二者偏差越小。因此利用集中系数和偏离系数对不同公式的计算结果进行比较和分析。集中系数及偏离系数分别定义为［9］

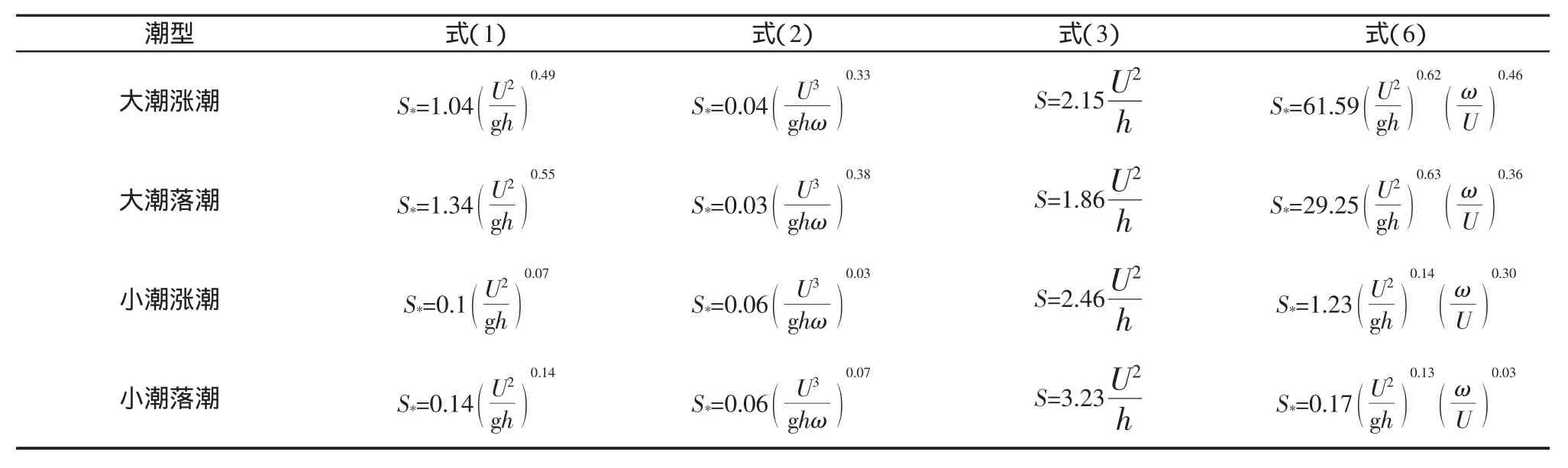
表1 不同挟沙力公式拟合结果Tab.1 Curve fitting results of different equations for sediment carrying capacity

式中：xi，yi分别为实测含沙量的值和利用各个公式计算所得到的挟沙力的值；n为实测资料的个数。

由图1～图6可知，式（1）～式（3）以及式（6）的计算结果与实测值相对较为接近，计算点基本分布在45°线的两侧，未出现较大偏离，总体而言，这4个公式能够用来拟合曹妃甸海域的挟沙力。但必须指出，式（4）和式（5）的计算结果与其余公式相比存在较大偏差，由于这2个公式是通过水文资料直接推算的方式来推求曹妃甸水域的挟沙力分布，没有利用当地的实测资料进行拟合计算，因此对准确反映当地水流和输沙之间的关系提出了更高的要求，虽然这2个公式曾应用大量资料进行验证，但资料范围有限，且由于水流输沙问题的复杂性，不仅存在区域性、季节性的变化，也存在年际等之间的差异，此外由于曹妃甸海域泥沙来源较少，水体处于非饱和挟沙状态，而式（4）和式（5）则主要反映水体的饱和挟沙能力，因此直接利用这2个公式推求某一时段某一区域的水流挟沙能力必然会带来较大的误差。由图4和图5可以看出，虽然式（4）和式（5）计算值与实测值存在一定的偏差，但总体而言，计算值和实测值基本还是分布于45°线附近，这一定程度上表明，当缺少实测资料的时候，利用这2个公式推求曹妃甸海域的挟沙能力还是可行的，推求得到的水体挟沙能力也具有一定精度。

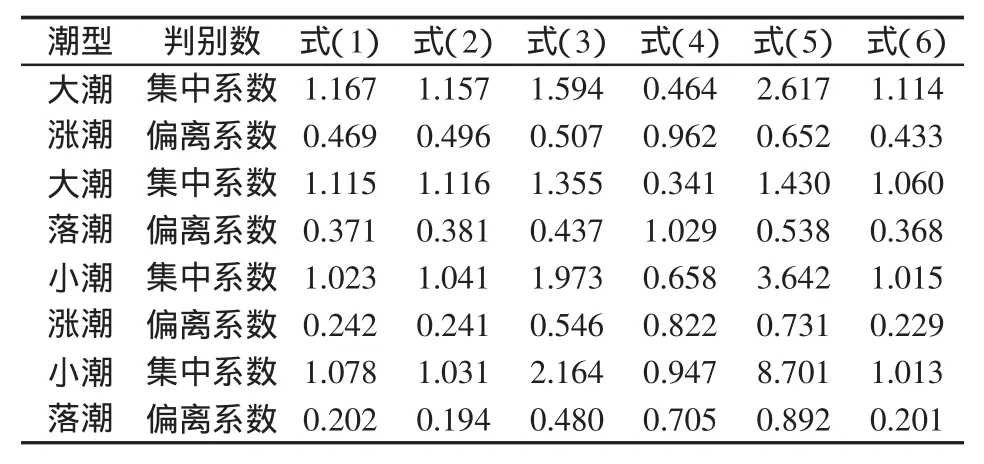
表2 统计所得对应各个公式计算结果与实测资料的集中系数和偏离系数的值Tab.2 Statistical corresponding results of each formula with concentration factor and deviation from the value of coefficient of the measured data

结合图表进一步比较式（1）～式（3）和式（6）之间的差异可知，集中系数较接近1的主要有式（1）、式（2）和式（6），而偏离系数较接近 0的同样为式（1）、式（2）和式（6），说明利用这3个公式计算得到的结果与实测值较为接近，精度相对较高。这也在一定程度上说明，曹妃甸水域的水流挟沙能力与表征水流强度的弗劳德数相关程度较高，但并不是线性相关，而是存在一定程度的非线性关系。

另外，比较式（1）、式（2）和式（6）的计算结果可进一步知道，利用式（6）计算所得到的结果与实测值最为接近，其集中系数和偏离系数的综合反映亦表明了这一点。但是需要指出的是，式（6）所反映出来的泥沙沉速越大挟沙力越大的特性与常规的认识相反，分析原因，可能受2个方面的影响：一方面是由于曹妃甸水域的泥沙颗粒相对较细（2006年夏季的悬沙现场采样颗分结果表明，曹妃甸海域大潮和小潮期间，悬沙中值粒径的平均值均在0.007 mm左右），主要属于粘性细颗粒泥沙范畴，此时泥沙在海水中主要以絮凝的形式沉降，沉速的变化幅度并不大，因此相对重力作用项ω/u并未能真实的反映一个潮周期内紊动作用与重力作用的相互对比关系；另一方面，由于本文采用的主要是夏季一次大潮和小潮测验期间的资料，数据样本的个数有限，同时由于泥沙的絮凝沉速远小于潮流速，由此导致相对重力作用项ω/u的值在一个潮周期内的变化幅度也远小于弗劳德数项u2/gh的值，因此当利用式（6）进行拟合时，由于样本个数的限制，所反映出来的弗劳德数项占的比重也远大于相对重力作用项，使得式（6）中的相对重力作用项无法真实的反映其对水流挟沙能力变迁的贡献。基于上述原因，利用式（6）推求曹妃甸水域水体挟沙力的适宜性还有待于进一步验证。

3 结语

通过利用曹妃甸的实测水文泥沙资料，就不同挟沙力计算公式在曹妃甸区域的适用性和精度进行了比较，得到如下结论：（1）利用实测资料拟合得到的挟沙力公式的计算结果普遍优于直接利用水文资料推算水流挟沙能力的计算公式得到的结果；（2）水流挟沙能力与表征水流强度的弗劳德数具有较高的相关性，但直接线性相关的程度不高，主要呈现一定程度的非线性相关，同时式（4）和式（5）的计算结果虽然与实测值相比偏差较大，但总体而言能反映曹妃甸海域的实际水流挟沙能力随水流的变化情况；（3）包含弗劳德数的挟沙力计算公式拟合实测含沙量的效果相对较好，其中式（1）、（2）、（6）的精度相对较高，虽然式（6）的精度相对最高，但由于其反映出来的沉速越大挟沙力越大的特性与常规认识存在偏差，因此还需要收集更多的资料对其适用性进行探讨。

［1］曹妃甸工业区管理委员会.加快曹妃甸开发建设努力成为拉动环渤海地区经济发展新引擎［J］.港口经济，2008（3）：42-44.

［2］尹延鸿.对河北唐山曹妃甸浅滩大面积填海的思考［J］.海洋地质动态，2007，23（3）:1-10.

［3］尹延鸿.曹妃甸浅滩潮道保护意义及曹妃甸新老填海规划对比分析［J］.现代地质，2009，23（2）：200-209.

YIN Y H.The Significance of Protection of the Caofeidian Shoal Tidal Channel and Comparison of the New Caofeidian Plan of Sea Reclamation Land to the Old One［J］.Geoscience，2009，23（2）：200-209.

［4］侯志军，杨晓阳，李岩.黄河口水流挟沙力计算方法研究［J］.人民黄河，2008，30（11）：49-51.

［5］刘家驹.在风浪和潮流作用下淤泥质浅滩含沙量的确定［J］.水利水运科学研究，1988（2）：22-26.

LIU J J.Determination of the Silt Concentration on Shoal Under the Action of Wind Waves and Tidal Currents［J］.Hydro-Science and Engineering，1988（2）：22-26.

［6］王昌杰.河流动力学［M］.北京：人民交通出版社，2001.

［7］浙江水利科学研究所.钱塘江河口潮流输沙经验公式的探讨［R］.杭州：浙江水利科学研究所，1963.

［8］窦国仁，董风舞，Xibing Dou.潮流和波浪的挟沙能力［J］.科学通报，1995，40（5）：443-446.

［9］张燕菁，胡春宏.黄河口输沙能力关系的探讨［J］.泥沙研究，1997（2）：46-50.

［10］黄仁勇，韦直林，赵连军，等.河床冲淤幅度判别指标和水流挟沙力公式验证［J］.人民黄河，2004，26（5）：22-24.