基于改进型UMP BP-Based算法的LDPC译码研究
2010-05-14张天瑜
张天瑜
(无锡市广播电视大学 机电工程系,江苏 无锡 214011)
在研究Turbo码的译码过程中,MacKay、Neal和Wiberg等人发现Gallager早在1962年提出的低密度校验LDPC(Low-Density Parity-Check)码是一种性能卓越具有渐进特性的非常好码,在加性高斯白噪声AWGN(Additive White Gaussian Noise)信道下的译码性能可以逼近Shannon信道容量的极限。由于LDPC码的校验矩阵为稀疏矩阵,实现译码的复杂度比Turbo码要低,在中长码长时的译码性能超过Turbo码,能够实现并行译码以及具有译码错误可检测的特点,并且比Turbo码更适合于高速无线数据业务,因此已逐渐被IEEE802.3an、IEEE 802.16e等标准所采纳。目前在国外LDPC码在下一代卫星数字视频广播标准DVB-S2(Digital Video Broadcasting-Satellite Second Generation)以及下一代移动通信LTE中得到了广泛的应用。在国内,中国移动多媒体广播 CMMB(ChinaMobileMultimediaBroadcasting)的信道编码技术的一个亮点就是采用了LDPC编码方案[1-7]。本文提出一种改进型UMP BP-Based译码算法,利用最小均方误差准则来计算该算法中的参数,能够在一定程度上弥补UMP BP-Based译码算法的性能缺陷。
1 LDPC码简介
LDPC码一般是用Tanner图来表示,Tanner图中的变量节点和校验节点对应于LDPC码校验矩阵H的列和行,Tanner图中的连线对应于LDPC码校验矩阵H的非零元素。校验矩阵H中每行非零元素的个数称为行重,每列非零元素的个数称为列重,所有行重相等并且所有列重也相等的码称为规则LDPC码;否则,称为非规则LDPC码。设LDPC码的校验矩阵为H如式(1)所示。根据H矩阵得到与之对应的Tanner图,如图1所示。图中 C1~C6表示校验节点,B1~B9表示变量节点。
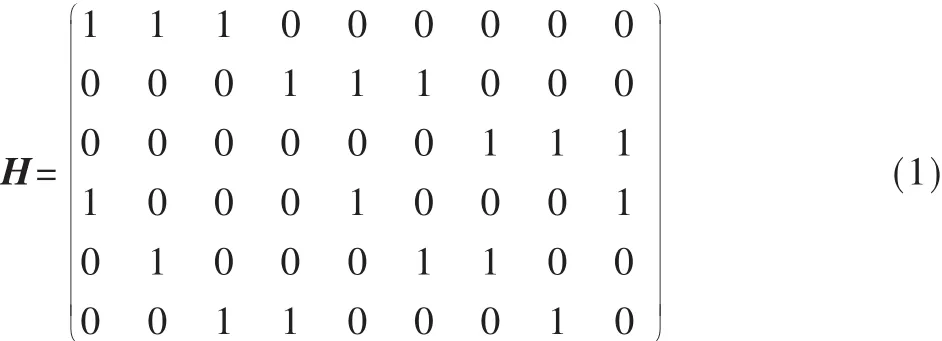
图1 H矩阵对应的Tanner图
由于非规则LDPC码的行重和列重不相等,因此在其对应的Tanner图中变量节点和校验节点的度数也就不完全相等,非规则LDPC码的译码性能较规则LDPC码的译码性能要高。这里节点的度数是指与该节点相连接的边的条数。为了表示非规则LDPC码,分别用序列λ=(λ1,λ2,…,λdv)和 ρ=(ρ1,ρ2,…,ρdc)表示变量节点和校验节点的边次数分布,其中,λi和 ρi分别表示 Tanner图中度数为i的变量节点和校验节点的边数在总边数中所占的比例,这里的下标dv和dc分别表示变量节点和校验节点的最大度数。非规则LDPC码的变量节点和校验节点的边次数分布除了用上述的序列表示之外,还可以表示为:


2 UMP BP-Based译码算法
UMP BP-Based译码算法和LLR BP译码算法的原理是相同的,都是通过迭代计算出校验节点和变量节点之间传递的信息,然后根据这些信息进行判决[8-12]。基于H矩阵的UMP BP-Based译码算法的原理图如图2所示。
设编码器的输出码字为 c=(c1,c2,…,cn),通过二进制相移键控BPSK(Binary Phase Shift Keying)调制后变为xi=2ci-1,经过AWGN信道,译码器的输入序列为r=(r1,r2,…,rn),其中,ri=2ci-1+ni,ni为均值为 0、方差为σ2的高斯白噪声。设N(m)={n|Hmn=1}为所有与校验节点Cm相连的变量节点;M(n)={m|Hmn=1}为所有与变量节点Bn相连的校验节点;N(m) 表示 N(m)中除去变量节点Bn所剩下的变量节点的集合;M(n)m表示M(n)除去校验节点 Cm所剩下的校验节点的集合;qij(b),b=0,1表示变量节点i传递给校验节点j的外部概率信息;rji(b),b=0,1表示校验节点j传递给变量节点i的外部概率信息。UMP BP-Based译码算法的具体步骤如下:
图2 基于H矩阵的UMP BP-Based译码算法的原理图
(1)初始化
计算信道传递给变量节点的初始概率似然比信息L(Pi),i=1,2,…,n。 对于变量节点 i以及与其相邻的校验节点j∈M(i)而言,在AWGN信道中得到变量节点传递给校验节点的初始信息为:
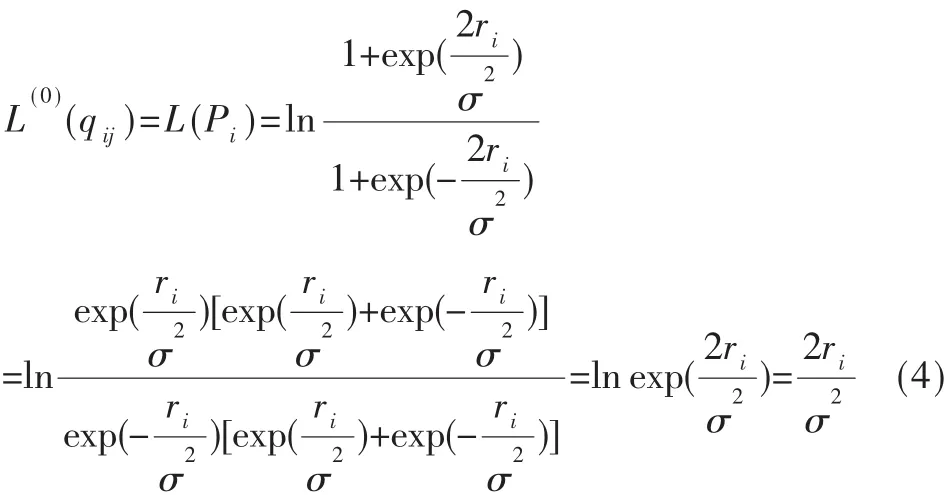
(2)节点信息的迭代处理
①校验节点的信息传递
对所有的校验节点j以及与其相邻的变量节点i∈N(j),在第k次迭代中,变量节点传递给校验节点的信息为:
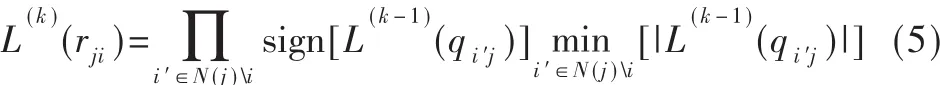
②变量节点的信息传递
对所有的变量节点i以及与其相邻的校验节点j∈M(i),在第k次迭代中,校验节点传递给变量节点的信息为:
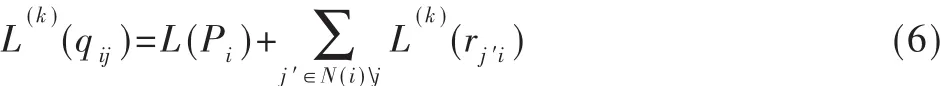
(3)判决译码
对所有的变量节点计算判决信息:
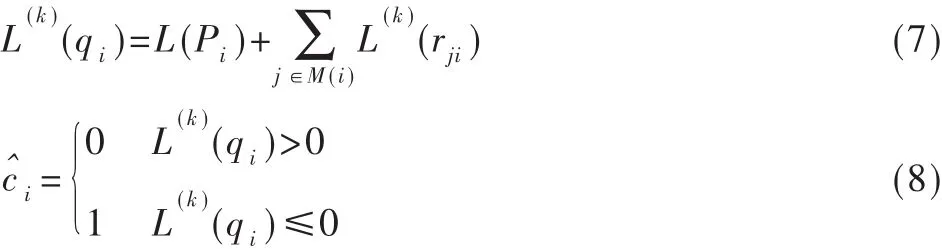
(4)停止
3 改进型UMP BP-Based译码算法
在LLR BP译码算法中,变量节点传递给校验节点的信息为:
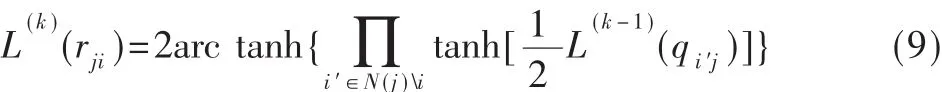
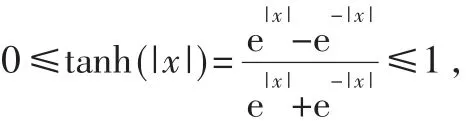
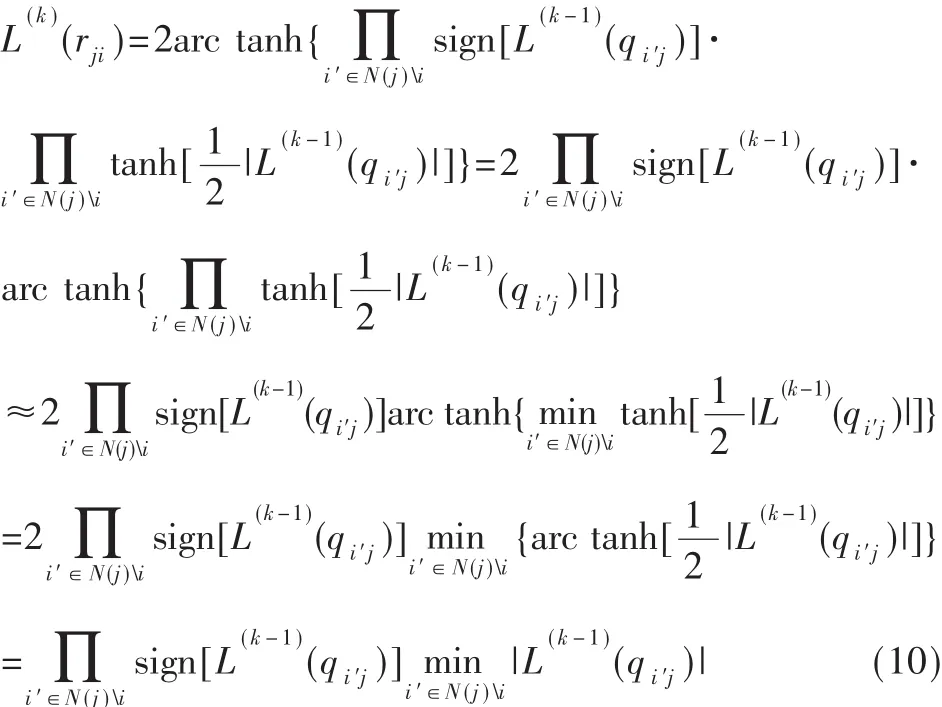
这样就得到式(5)所描述的UMP BP-Based译码算法。由于是利用式(10)来近似代替式(9),本文可以大大简化运算,但是两者之间的误差将导致译码性能有所下降。为了减少这种误差,通常采用Normalized BP-Based译码算法和Offset BP-Based译码算法。Normalized BPBased译码算法是通过引入归一化因子来减小误差,而Offset BP-Based译码算法是通过引入偏移因子来减小误差。这两种译码算法虽然能在一定程度上减小了误差,但是误差减小的程度有限,并且引入的因子只能通过仿真确定,具有偶然性。
本文提出一种改进型UMP BP-Based算法,利用最小均方误差准则,通过引入参数 α、β、γ使得校验节点的信息的均方误差最小。为了叙述方便,将式(5)记为L2,式(9)记为 L1,改进型 UMP BP-Based算法中校验节点的信息记为L3。这里用含有L2的表达式来表示L3,即设定|L3|=α+β|L2|+γ|L2|2,通过改变参数 α、β、γ,使得|L3|和|L1|的均方误差最小。 设 g(α,β,γ)为 L3和 L1的均方误差,则:
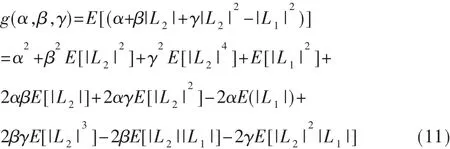
为了求出参数 α、β、γ,使得 g(α,β,γ)达到最小值,分别对式(11)中的 α、β、γ 求偏导数:

将式(11)代入式(12),可得:

4 仿真实验与结果分析
首先在Matlab软件中构造码长为1 806、码率为1/2、列重为3、行重为3的规则LDPC码,即变量节点的度数为 3,校验节点的度数也为 3,λ(x)=ρ(x)=x2。 采用BPSK调制,经过AWGN信道,每次译码算法中的最大迭代次数都设置为80次,然后通过蒙特卡罗算法求解出式(15)中相关参数的数学期望 E[·],通过仿真得到 α=212.32,β=0.93,γ=0.12。 改进型 UMP BP-Based译码算法以及UMP BP-Based译码算法、NormalizedBP-Based译码算法和OffsetBP-Based译码算法的性能曲线如图3所示。
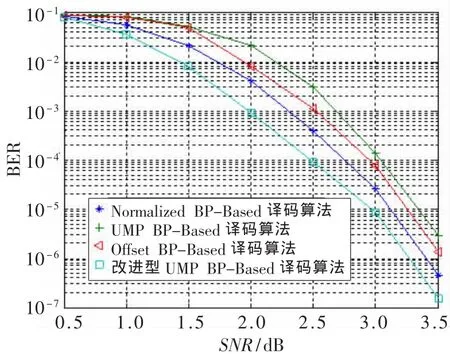
图3 4种译码算法的性能比较曲线
从图3可以看出,在相同误码率BER(Bit Error Rate)(BER=10-5)的情况下,改进型UMP BP-Based译码算法的信噪比 SNR(Signal-to-Noise Ratio)比 UMP BP-Based译码算法的SNR节省将近0.4 dB,比Normalized BPBased译码算法和Offset BP-Based译码算法的SNR分别节省0.1 dB和0.2 dB。由此说明改进型UMP BP-Based译码算法在上述的4种译码算法中具有更好的性能。
由于UMP BP-Based译码算法中校验节点的信息传递公式是对LLR BP算法中校验节点的信息传递公式的近似,所以UMP BP-Based译码算法的性能在一定程度上有所下降。本文提出一种改进型UMP BP-Based译码算法,该算法的创新之处在于,利用最小均方误差准则推导出了一个更加近似的公式,能够进一步降低由于近似计算带来的误差,并且对所有的LDPC码的译码具有通用性。这在LDPC码的应用领域,具有一定的实用价值。
[1]YANG K, FELDMAN J, WANG X D.Nonlinear programming approaches to decoding low-density parity-check codes[J].IEEE Journal on Selected Areas in Communications, 2006,24(8)∶1603-1613.
[2]SWAMY R, BATES S, BRANDON T L, et al.Design and test of a 175-Mb/s, rate-1/2(128,3,6)low-density paritycheck convolutional code encoder and decoder[J].IEEE Journal of Solid-State Circuits, 2007,42(10)∶2245-2256.
[3]LIU L, SHI C J R.Sliced message passing∶high through-put overlapped decoding of high-rate low-density paritycheck codes[J].IEEE Transactions on Circuits and Systems I∶Regular Papers, 2008,55(11)∶3697-3710.
[4]HONG S N, KIM S, SHIN D J, et al.Quasi-cyclic lowdensity parity-check codes for space-time bit-interleaved coded modulation[J].IEEE Communications Letters, 2008,12(10)∶767-769.
[5]CHEN H Y, LIN M C, UENG Y L.Low-density paritycheck coded recording systems with run-length-limited constraints[J].IEEE Transactions on Magnetics, 2008,44(9)∶2235-2242.
[6]GONG C, LIU Q, CUI H J, et al.Switch-type hybrid hard decision decoding algorithms for regular low-density parity-check codes[J].IEEE Transactions on Information Theory, 2008,54(7)∶3181-3188.
[7]RAZAGHI P,YU W.Bilayer low-density parity-check codes for decode-and-forward in relay channels[J].IEEE Transactions on Information Theory, 2007,53(10)∶3723-3739.
[8]PISHRO-NIK H,FEKRI F.Results on punctured lowdensity parity-check codes and improved iterative decoding techniques[J].IEEE Transactions on Information Theory,2007,53(2)∶599-614.
[9]HONARY B, MOINIAN A, AMMAR B.Construction of well-structured quasi-cyclic low-density parity check codes[J].IEE ProceedingsofCommunications, 2005,152(6)∶1081-1085.
[10]SADEGHI M R, BANIHASHEMI A H, PANARIO D.Low-density parity-check lattices∶construction and decoding analysis[J].IEEE Transactions on Information Theory,2006,52(10)∶4481-4495.
[11]KIM N, KIM J, PARK H, et al.An improvement of UMP-BP decoding algorithm using the minimum mean square error linear estimator[J].ETRI Journal,2004,26(5)∶432-436.
[12]KIM N,PARK H.Modified UMP-BP decoding algorithm based on mean square error[J].Electronics Letters,2004, 40(13)∶816-817.
