一种基于级联混沌系统的图像加密算法

景运革，王彩霞

(运城学院 公共计算机教学部，山西 运城 044000)

目前混沌加密己成为密码学研究的热点之一，但已有的大部分混沌加密算法都是基于单个混沌系统的。事实表明，一些混沌映射可通过相空间重构的方法精确预测出来[1]。另外，由于计算机精度的限制，单混沌系统输出的时间序列并不能达到理论上的完全随机，而可通过多个混沌系统的级联使这一缺陷得到改善[2]。为此，本文提出了一种基于多混沌系统级联的图像加密算法，理论分析与数值实验均表明本算法能够达到密码学要求的混淆和扩散的目的，并能有效地预防差分攻击。

1 混沌序列的生成

1.1 Logistic映射

Logistic映射由数学生态学家May于1976年提出，是非线性迭代方程和研究最广泛的动力系统。Logistic映射的定义为：

当3.569 945 6<μ≤4时，Logistic映射工作处于混沌状态，即由初始条件x0在Logistic映射的作用下所产生的序列{xk}是非周期、不收敛的，并对初始值非常敏感；当μ=4时，该映射是满射，产生的混沌序列在区间(0，1)上具有遍历性。由于Logistic映射具有与白噪声相似的特性、简单和初始值敏感性的特点，因此很多混沌图像加密算法都是基于Logistic映射的。

1.2 时空混沌映射

时空混沌系统是一个空间上的扩展系统[3]，它展现了时间和空间上的混沌性。耦合映射格子(CML)通常被作为时空混沌系统使用，这种系统是具有离散时间、离散空间和连续状态的动力系统。它由位于格子站点上的称为局部映射的非线性映射组成，每个局部映射与其他局部映射以一定规则进行耦合连接。由于每个局部映射所固有的非线性动力特性及相互间耦合所产生的发散性，CML可以展现时空混沌性。所以采用不同的局部映射和耦合方法便可以构造出不同形式的CML[4]。本算法构造的二维CML为：

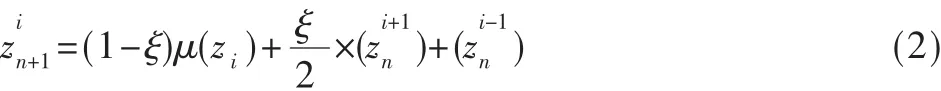
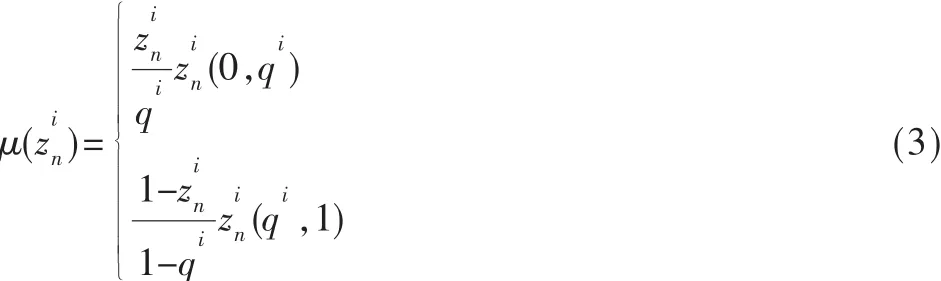
2 加密与解密的实现

本算法选用的混沌系统为时空混沌系统与一维Logistic映射。首先利用式(2)时空混沌系统产生随机序列，然后将这个序列值分别作为式(1)的Logistic映射初始值，经过特定次数的迭代以后得到最后所需的混沌序列。这个特定次数是由上一个图像像素加密后的结果决定的。

2.1 加密过程

假设待加密的数字图像为z(M×N)。首先，将图像 z中的像素值从左到右、从上到下进行横向扫描，将扫描得到的像素值存储到f(n)中。加密过程如下：

(2)对第i和i+1个像素加密时，首先将si作为式(1)的初值进行特定次数的迭代得到k。假设前两个已加密的像素值分别为c(i-2)和c(i-1)，则求 k所需要的迭代次数为：

n=(c(i-2)+c(i-1))mod 25，其中当 n=0时，迭代 25次。K的二进制形式表示为∶

k=0b1(k)b2(k)……bi(k)……k∈(0，1)bi(k)∈{0，1}。第i个比特bi(x)可由下式得到：

经计算可得到一个16位的比特序列，取前8位作为key1与第i个像素值进行“异或”操作得到密文c1(i)，取后8位作为key2与第i+1个像素值进行“异或”操作得到密文 c1(i+1)。

(3)对第1个和第2个像素值加密时，首先用由时空混沌系统式(2)产生的随机序列s(1)作为初值进行迭代25次，将由步骤(2)得到的 key1、key2分别与对应的像素值进行“异或”操作得到密文c1(1)和c1(2)，然后按步骤(2)依次对图像中的每个像素进行操作，最后可以得到图像c1。

(4)对图像c1按相反的方向从最后两个像素开始按步骤(3)对像素值进行操作得到图像c，即为加密后的密文图像。

2.2 解密过程

解密过程与加密过程相反，即：将步骤(2)中提到的迭代的次数改为由密文图像的前两个像素值决定，再将步骤(3)与步骤(4)的顺序颠倒过来，即可完成密文图像的解密。

2.3 实验结果

利用本文提出的算法，令Logistic映射的参数μ=4，ξ=0.99，时空混沌映射的初始值x=0.421 52、x=0.639 42、x=0.533 46、q1=0.327 54、q2=0.525 12 和 q3=0.832 14，对256×256的图1(a)进行加密。图1(c)即为加密后的结果。图1(b)和图1(d)分别是待加密图像和已加密图像的直方图。

3 安全性分析

本算法有很高的安全性，具有更大的密钥空间，且能够抵御大部分常见的攻击。

3.1 密钥空间分析

3.2 密钥敏感性的测试

图2给出了密钥敏感性的测试结果。其中图2(a)是用正确密钥 x=0.421 52、x=0.639 42、x=0.533 46、q1=0.327 54、q2=0.525 12和 q3=0.832 14进行解密后所得到的图像；图2(b)和图2(c)分别是将密钥中 x和 x改为0.421 53与0.639 42时解密后所得到的图像。将图2(b)和图2(c)与图2(a)进行比较，可见虽然密钥仅发生了非常微小的改动，但是解密后的结果却完全不同，这表明本算法对密钥是敏感的。

3.3 统计分析

图像中相邻像素的相关性非常大，在加密过程中为了防御统计攻击，必须使得相邻像素间的相关性降低[5]。本文在待加密图像和加密后的图像中各随机地选取了2 008对像素对，测试其水平方向、垂直方向、对角方向的像素相关性，并利用式(8)计算其相关系数：

表1 相邻像素值的相关系数rxy

3.4 差分攻击分析

通过对待加密图像做微小的改变，然后观察该改变带来的结果的方法，攻击者可以获得加密后图像与原图像之间的关联。若某加密算法可使原图像发生微小变化，使前后加密的结果变化很大，则该算法即可很好地预防差分攻击。

像素数目改变率(NPCR)是指当待加密图像改变一个像素时，加密后图像像素数目的改变率。NPCR越大，表明加密算法对于待加密图像变化越敏感，则该加密算法抵抗明文攻击能力越强；平均强度变化率(UACI)是指待加密图像和加密后图像相应像素的平均强度的变化率，该指标越大，表示加密后图像与待加密图像比平均强度变化越大，则该加密算法抵抗差分攻击能力越强。设两幅加密后的图像分别为c1和c2，则：

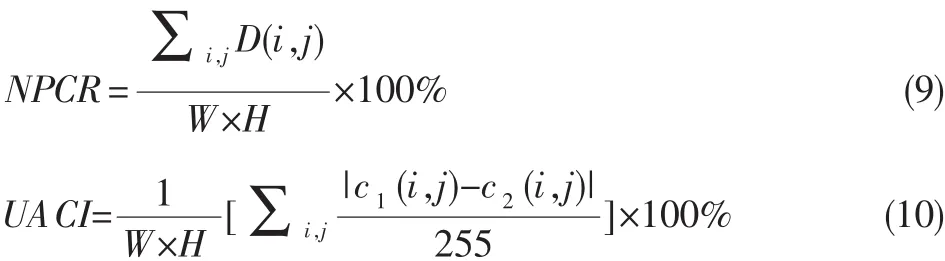
式 中，c1(i，j)、c2(i，j)分 别 表 示(i，j)处 的 像 素 灰 度 值，W 为图像的宽度，H为图像的高度。定义矩阵D(i，j)：若c1(i，j)=c2(i，j)，则 D(i，j)=0；否则 D(i，j)=1。

选取Lena原图像图1(a)作为测试对象，随机选取其中某个像素点并改变它的像素值，然后用本算法对这两幅差别微小的图像加密，分析加密后图像相同像素的比率。 经计算得到 NPCR=99.653 7%，UACI=37.682 5%，表明了即使将待加密的图像做微小的改动，通过本算法加密后，也会得到明显的差异。

3.5 信息熵攻击

信息论是研究信息传输与信息压缩的数学理论，最早由香农在1949年提出[6]。信息论中一个非常重要的概念就是信息熵，一个信息源m的信息熵：

式中，P(mi)表示信号mi出现的概率。对于给定的一个实际信息源很少能够产生随机的信息，所以通常它的熵值小于理想值。在对信息加密后，一般希望它的熵H(m)=8。若加密后的信息熵值小于8，则会威胁到所加密图像的安全性。

利用本算法对图2(a)进行加密得到图2(c)，记录图2(c)中每一个不同像素值，并计算其出现的概率，最后可求出：

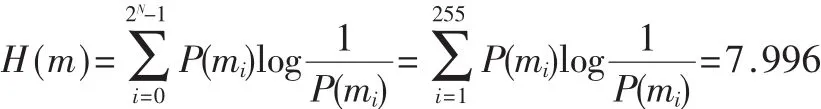
本文提出一种基于级联混沌系统的图像加密算法，采用由Logistic映射构成的一维CML作为时空混沌系统，然后将它的输出序列作为Logistic由某一初始值经过特定次数的迭代后得到最终的密钥序列。安全性分析表明，本算法的密钥空间足够大，使得暴力攻击不可能。仿真实验结果也表明，本算法具有较高的性能，在图像加密和图像传输中具有一定的潜在应用价值。

[1]ZHANG S， XIAO X C.Prediction of chaotic time series by using adaptive higherorder nonlinear fourier infrared filter[J].Acta Physica Sinica， 2000，49(7)∶1221-1227.

[2]KACHRIS C， BOURBAKIS N， DOLLAS A.A reconfig-urablelogic-based processorfortheSCAN imageand video encryption algorithm[J].International Journal of Parallel Programming， 2003，31(6)∶489-506.

[3]XIANG T， LIAO X F， TANG G P.A novel block cryptosystem based on iterating a chaoticmap[J].Physics Letters A， 2006，349(1)∶109-115.

[4]LI P， LI Z， WOLFGANG A.A stream based on a spatiotemporal chaotic system[J].Chaos，Solitons and Fractals，2007，32(5)∶1867-1786.

[5]孙伟.关于Arn01d变换的周期性 [J].北方工业大学学报，1999，11(1)：29-32.

[6]SHANNON C E.Communication theory of secrecy systems[J].Bell Syst Tech J， 1949，28：656-715.