橡胶集料混凝土渗透性机理研究

□文/张 伟

橡胶集料混凝土渗透性机理研究

□文/张 伟

文中基于Darcy定律和Young-Laplace方程，研究了橡胶集料混凝土渗透性机理。通过对2种轮胎橡胶的水接触角测定，分析了橡胶集料对毛细孔压力的影响。结果表明，橡胶的水接触角介于80°～116°之间疏水性明显，由此计算的橡胶集料混凝土毛细孔压力较普通混凝土降低了38.1%～80.2%；橡胶集料混凝土的真实渗水速率受外部静水压力、毛细孔压力以及毛细孔孔径的影响。

橡胶集料；渗透性；混凝土；毛细孔压力

橡胶集料混凝土是一种将废旧轮胎破碎后作为集料并以一定比例替代细骨料或粗骨料配制而成的新型水泥混凝土，是一种多相水泥基复合材料。目前，已经发现橡胶集料混凝土具有高韧性和很好的抗裂性[1]，很大的阻尼比[2]、较高的吸声系数和较低的导热系数[3]等优点；另一方面橡胶集料混凝土的耐久性，尤其是抗渗性的高低对于橡胶集料混凝土能否应用于工程实践具有重要意义。天津大学胡鹏等人[4]采用渗透深度法对0～150kg/m3橡胶集料掺量的混凝土进行了试验，发现橡胶集料混凝土的平均渗水高度小于普通混凝土，渗透系数达到了4.09×10-13m/s，而对于橡胶集料混凝土产生高抗渗性的机理目前尚未有令人满意的解释。

传统上，水在混凝土内的渗透被视为压力梯度作用下多孔介质中液相的渗透过程，通常用Darcy定律加以解释，混凝土抗渗性的高低取决于渗透系数，而渗透系数与混凝土的孔结构、孔隙饱和度以及外部温湿度等多种因素有关，一般认为混凝土内最可几孔径越小则混凝土的抗渗性越好。然而，实际上只要混凝土与水接触，即使不存在静水压力，由于毛细孔压力作用，也会有渗透现象发生，毛细孔压力由Young-Laplace方程确定，其大小受毛细孔孔壁亲水性强弱（水接触角大小）的影响。因此，本文针对真实橡胶集料混凝土渗透机理进行研究，探讨橡胶的水接触角对毛细孔压力的影响，同时还对毛细孔压力和静水压力共同作用下的橡胶集料混凝土渗透过程进行分析。

Darcy定律与渗透系数

式中：dq/dt——渗水速率，m3/s；

k——渗透系数，m/s；

A——透水面积，m2；

Δh——静水压力，m；

L——多孔介质的厚度，m。渗透系数k的物理意义是一定厚度的材料在单位水压差作用下，在单位时间内透过单位面积的水量。我国现行规范中混凝土渗透系数是按照SL352-2006《水工混凝土试验规程》中计算得到的，如图1。

在静水压力作用下水在多孔介质中产生的稳态定向流动满足Darcy定律[5]。

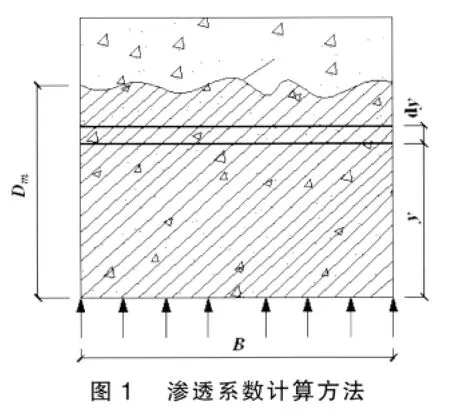
混凝土受到向上的静水压力Δh作用，设时间为t时，饱和水面上升高度为y，则该处压力梯度为Δh/y；按照Darcy定律，水面上升速度为dq/dt=kΔh/y，设时间增量dt，水面升高dy，混凝土孔隙率为m，水面宽度为B，则水量增量为dq=mBdy=BkΔhdt/y，压水时间T时水面上升到Dm，两边积分：

则可得渗透系数：

Darcy定律用于描述实际橡胶集料混凝土发生的渗透还有一定困难。其一，Darcy定律没有考虑毛细孔压力的作用，根据文献[6]的研究结果，当相对湿度在80%～100%时，硬化水泥浆体内部毛细孔压力最高可达30MPa，这一数值远大于抗渗试验中采用的静水压力；其二，实际混凝土的渗水过程是混凝土内部气相、液相压力的平衡过程，因此，渗水速率是沿渗透方向变化的，即表层渗透与内部渗透的速率是不同的；此外，用于计算渗透系数的孔隙率是一经验值，而混凝土的孔隙率有时会相差很大。这些都造成了Darcy定律不能直接用于解释橡胶集料混凝土的渗透性。

橡胶集料混凝土渗透性分析

橡胶集料对毛细孔压力的影响

毛细孔压力是水在混凝土中渗透的一种主要驱动力，来源于毛细作用。由于液体表面存在着张力，为了达到毛细管道内液面两侧压力的平衡而发生液体整体流动的现象称为毛细作用。例如：混凝土桥墩水位以上区域发生锈蚀的原因就在于所谓的“灯芯”效应导致水渗透进入水面以上的位置，而“灯芯”效应的实质就是由毛细作用产生的。毛细孔压力的大小取决于毛细孔孔壁的亲水性强弱（水接触角）以及孔径的大小。如图2（a）所示，取混凝土毛细孔中的微液面作为研究对象，为了保持液面稳定，液面外的空气压力Pg和液体内部压力Pl差必须与液体表面张力γ所产生的提升力相平衡[7]，表示为

式中：Pg-P1——毛细孔压力，Pa；

θ——毛细孔孔壁的水接触角，(°)；

Ra、Rb——液面两个方向上的曲率半径，；由于毛细孔孔径远小于长度，可认为Ra=Rb=r。

由式（4）可得到Young-Laplace方程

式（5）是液体表面张力所提供的提升力F，即

对橡胶集料混凝土，如图2（b），其提升力来自于水泥石F1和橡胶集料F2共同作用，F可近似表示为

将式（7）带入式（5）可得

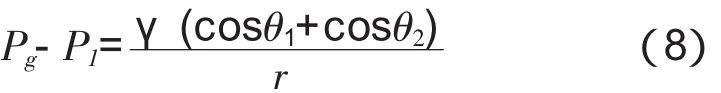
式中：θ1——水泥石的水接触角，(°)；

θ2——橡胶集料的水接触角，(°)。

因此，橡胶集料混凝土毛细孔压力大小受橡胶集料水接触角余弦值大小影响。

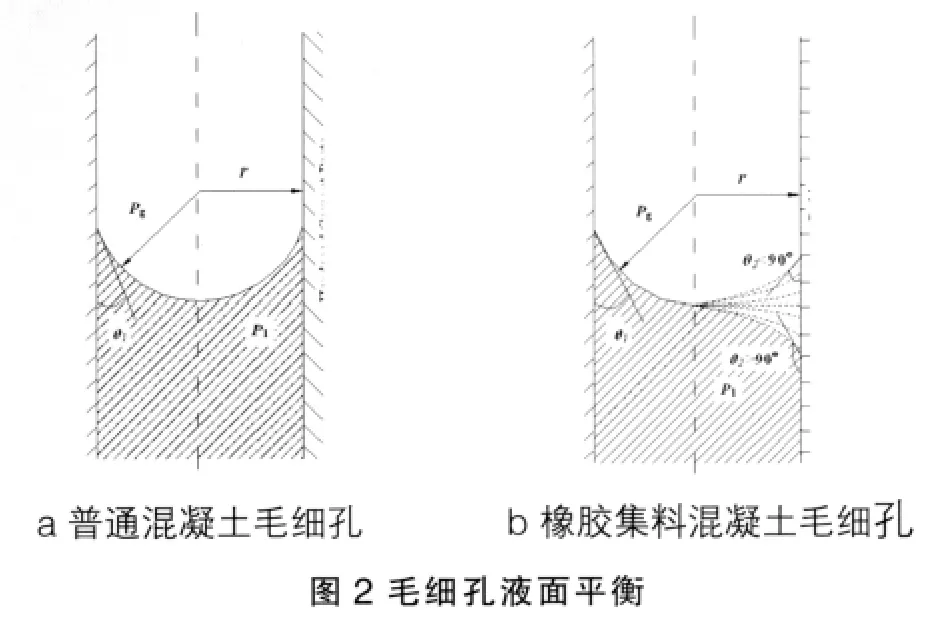
橡胶水接触角的测定

水接触角测定方法主要分3步。首先利用小液滴球冠法获得水接触角的原始图像，然后利用高斯-拉普拉斯运算滤波器（LOG）对所有的图像进行外形分析拟合得到液滴轮廓线，最后用多项式拟合方法计算出水接触角。

橡胶试样分别采用了轿车子午胎胎面胶（PT-1）以及载重子午胎胎面胶（TT-1），2种胶的配方组分见表1。橡胶试样规格为直径50mm，高10mm圆柱体。每种橡胶试样的测试面分为平滑面和粗糙面。粗糙面是光滑面经100#砂纸打磨所得到。此外还成型了相同尺寸的水泥石试样进行对比测试，采用P·042.5水泥，水灰比为0.45，标养至90d。

表1 试验用橡胶配方份

用微量注射器在固体表面上产生4μL的液滴，约0.5s后液滴即可达到稳定状态，1s时用高速CCD进行图像采集，所得图像见图3。

用MATLAB图像处理工具箱读入原始图像并将图像以RGB格式存储，为得到轮廓线数据，将RGB格式转换为灰度格式，然后利用高斯-拉普拉斯（LOG）算子先平滑掉噪声，再进行边缘检测[8]。对图像的平滑采用的是二维高斯函数G(x,y)

其中δ为高斯函数的空间分布系数开口范围，对该函数取拉普拉斯变换，即对高斯函数取二阶方向导数，得到二维LOG算子的函数形式

用LOG算子对输入图像I(x,y)进行卷积运算后就可得到液滴轮廓线。

水接触角计算一般以接触点Xcontact向液滴内延伸0.5mm水平距离的有效像素作为回归数据[9]，提取了该范围内（150Pixel）的数据进行多项式曲线拟合

式中：多项式系数ai采用最小二乘算法计算；n为多项式阶次，取1～4[9]；则水接触角可计算如下：

如表2所示，橡胶的水接触角大于水泥石；对于同种橡胶，水接触角大小还受表面粗糙程度的影响，粗糙表面的水接触角大于平滑表面，两种橡胶粗糙表面的水接触角值都＞110°，疏水性显著，而粗糙的表面特征与橡胶集料经机械破碎、研磨后的特征是相近的。

表2 水接触角测试结果 （°）

由式（8）可知，当水接触角 θ2＜90°，cosθ2＞0 时，橡胶集料孔壁提供提升力F2＞0。该力虽然是有利于毛细作用，但与水泥石的水接触角相比已有了很大的降低。而当 θ2＞90°，cosθ2＜0 时，橡胶集料孔壁则表现出对毛细作用的阻碍F2＜0。根据表2的结果，在孔径r和水的表面张力γ相等的情况下，采用表2中4个橡胶的水接触角，可以计算出所对应的橡胶集料混凝土毛细孔压力较普通混凝土分别降低了38.1%、77.9%、51.6%和80.2%。毛细孔压力的降低必然会导致渗水速率降低，进而增强混凝土的抗渗性。

毛细孔压力与静水压力共同所用下的渗透规律

综合考虑橡胶集料混凝土实际的毛细孔压力、静水压力，提出了如下的渗透方程

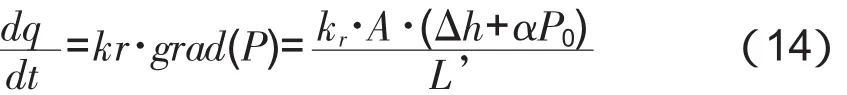
式中：kr——橡胶集料混凝土的渗透系数，m/s；

grad(P)——毛细孔压力和静水压力形成的总压力梯度；

Δh——橡胶集料混凝土所受的静水压力，m；

L’——实际渗透深度，m；

P0——按普通混凝土计算的毛细孔压力，m，

α——橡胶集料对毛细孔压力的影响系数

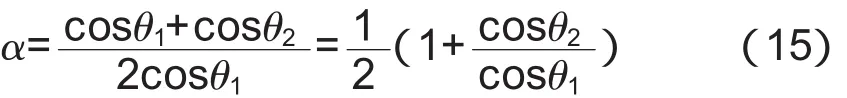
随着渗透深度和毛细孔半径的变化，根据式（14）对静水压力 Δh=0，0＜Δh＜αP0及 Δh＞αP0进行分析。

（1）当 Δh=0 时，dq/dt=krAαP0/L'。这种情况是单纯的毛细渗透过程，渗水速率与毛细孔压力成正比，当表层混凝土与水接触时，由于毛细作用，水迅速渗入，此时毛细孔半径越小则毛细孔压力越大，渗水速率越高。对于橡胶集料混凝土，橡胶集料的水接触角越大，则导致的毛细孔压力降低越大，表层混凝土的渗水速率越慢。

当水继续向混凝土内部渗透时，毛细孔液面达到平衡，此时所达到的渗透深度即为临界渗透深度，以L0表示。在临界渗透深度以内，橡胶集料水接触角越大，毛细孔半径越大，则毛细孔压力越小，混凝土的渗水速率越慢。

（2）当0＜Δh＜αP0且渗透时间足够时，必然有L'＞L0，由于静水压力的存在表层混凝土的渗水速率必然增加，但是由于所施加的静水压力小于毛细孔压力，实际渗透深度超出临街渗透深度的幅度并不大，表示为L'-L0＜L0。

（3）当 Δh＞αP0且渗透时间足够时，则L'＞L0且L'-L0≥L0。水继续被压入混凝土内部，由于实际混凝土中的孔结构并非平行连通管状孔隙，孔的形状和直径随深度不断变化，见图4。

当毛细孔孔径小到能够被吸附水阻塞时，静水压力Δh不断增加，会导致毛细孔内气相压力Pg不断增大，当Pg=Pl时，θ=90°，此时毛细作用消失；而当静水压力再增大时，则毛细孔压力的作用方向也会随之发生改变[10]，由原来的与静水压力作用方向相同变为与之相反，原先促使渗透加快的毛细孔压力，阻碍渗透且毛细孔半径越小，阻碍作用越大。此时，无论是混凝土的瞬间渗水速率还是在实际渗透深度内的平均渗水速率都会随着毛细孔半径的减小而变慢。

因此，用式（14）计算得到的橡胶集料混凝土渗透系数是随着实际渗透深度变化而呈非直线变化的变量。当发生毛细孔压力反向作用时，会导致混凝土的平均渗水速率显著降低。事实上，静水压力和临界渗透深度决定了毛细孔半径对渗水速率影响的正负效应。

结论

（1）测得轿车和载重车胎面胶水接触角介于80°～116°，由此计算的橡胶集料混凝土毛细孔压力较普通混凝土降低了38.1%～80.2%，橡胶集料混凝土的抗渗性相应地增强。

（2）对静水压力 Δh=0，0＜Δh＜αP0和 Δh＞αP0情况下橡胶集料混凝土的渗透规律分析表明，随着静水压力增高，毛细孔压力作用方向也会随之发生改变，阻碍水的渗透且孔径越小阻碍作用越大。

[1]M.M.Reda Taha，A.S.El-Dieb，M.A.AbdEl-Wahab，etal.Mechanical,fracture,andmic rostructal investigati on sofrubb erconcrete[J].Journal of Materialsin Civil Engineering,2008,20(10)：640-649.

[2]许静.橡胶集料混凝土阻尼测试及框架结构设计分析[D].天津：天津大学,2007.

[3]Piti Sukontasukkul,Piti.Use of crumbrubber to improve the rmal and sound properties of pre-cast concrete panel[J].Construction and Building Materials,2009,23（2）：1084-1092.

[4]胡鹏，朱涵，王旻.橡胶集料混凝土渗透性能的研究[J].天津理工大学学报，2006，22（4）：8-12.

[5]Christensen BruceJ,Thomas OMason,Hamlin MJenn ings.Comparison of measured and calculated perme abilities for hardene dcement pastes[J].Cement and Concrete Res earch，1996,26（9）：1325-1334.

[6]HuaC,AckerP,Ehracher A.Analyses and models of autog enous shrinkage of hardening cementpaste[J].Cement And Concrete Research,1995,25（7）：1457-1468.

[7]Seheidegger AE.Physics of flow through Porousmedia[M].Toronto：University of Toron to Press，1974.

[8]Gonzalez R,Woods R.数字图像处理[M].北京：电子工业出版社,2003.

[9]BateniA,Susnar SS,AmirfazliA，etal.Ahigh-accuracy polynomial fittin gapproach to determine contactangles[J].Colloid Surface A：Physico chemical and Engineering As pects，2003,219(1/3)：215-219.

[10]A.E.谢依金.水泥混凝土的结构与性能[M].北京：中国建筑工业出版社,1984.

book=38,ebook=5

TU528

B

1008-3197（2010）01-34-05

2009-12-31

张 伟/男，1978年出生，助理工程师，硕士，天津城投建设有限公司，从事工程技术管理工作。