非线性元件算法的建模与仿真

王 葵，商 莹

（1.山东大学，济南 250013;2.山东电力工程咨询院有限公司，济南 250061）

0 引言

电磁暂态程序（EMTP）最初版本Transients Program（TP），是H.W.Dommel在60年代后期完成的。我们也称EMTP为Dommel-Meyer（DM）scheme。DM结合了贝瑞隆Bergeron方法和梯形法，形成了求解暂态过程的一整套算法。此方法可以求解集中参数或分布参数的单相或多相网络方程[1]。

最常见的非线性元件有非线性电感和非线性电阻。EMTP用补偿法和分段线性化法2种技术解决非线性问题。分段线性化就是把非线性元件的特征曲线用几段具有不同斜率的直线段来表示，即把曲线近似的等值为折线。补偿法是将非线性元件看成电流源，将不含非线性元件的线性部分做戴维南等效，最后应用叠加原理得出最后结果[2]。

本文将在介绍非线性电阻和非线性电感的基础上，对三角形连接的非线性网络进行理论证明和仿真。新方法具有普遍性，可以扩展EMTP的节点分析法，使之容纳更多数量的非线性元件[3]。

1 非线性元件分析

1.1 非线性元件

非线性元件如图1所示。

图1 与线性网络连接的非线性元件电路

电流ikm必须满足以下2个方程：

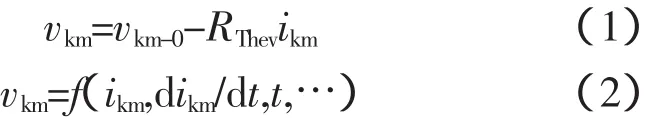
下标0表示无非线性元件时的电压，即戴维南开路电压。RThev是线性部分等效电阻。方程（2）是非线性元件特性方程。

如果方程（2）是解析表达式，就要用牛顿法迭代求解。如果方程（2）是将非线性元件应用分段线性化技术处理的，则无需迭代就可以找到2条曲线的交点[4]。如图2所示。

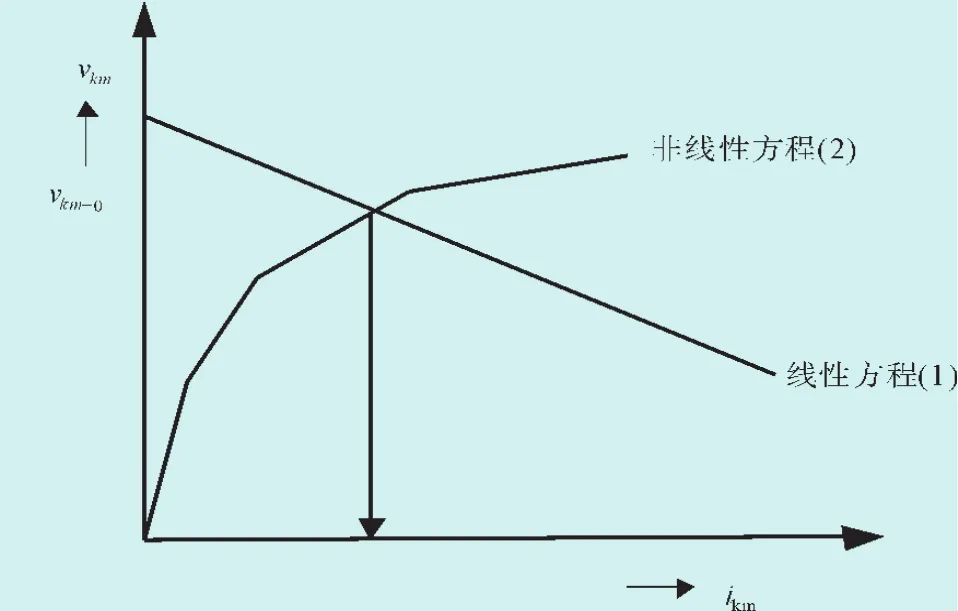
图2 2个方程的联立解

对于含有多个非线性元件的电路，如图3所示，我们首先计算戴维南等效电路。

图3 与线性网络连接的非线性元件电路

对每一个非线性元件，从线性网络中流出的电流等于流入的电流。

1.2 EMTP的局限

EMTP补偿法要求流入非线性元件的电流等于流出的电流。在如图4的情况下，非线性元件类似三角形连接，使得Ia≠Ia′，因此，EMTP补偿法无法计算戴维南等效电阻。在EMTP中三角形连接的真的非线性元件是无法运行的[5]。

图4 类似于三角形连接的非线性元件电路

2 牛顿-拉夫逊法非线性元件模型

图5（a）中假定非线性电感和非线性电阻是电流控制型的。图5的状态方程为

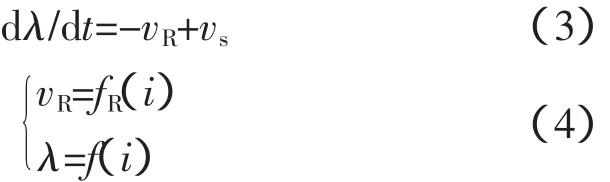
解：第一步是用数值计算公式将方程离散化，并且写作代数方程。应用梯形公式可得，

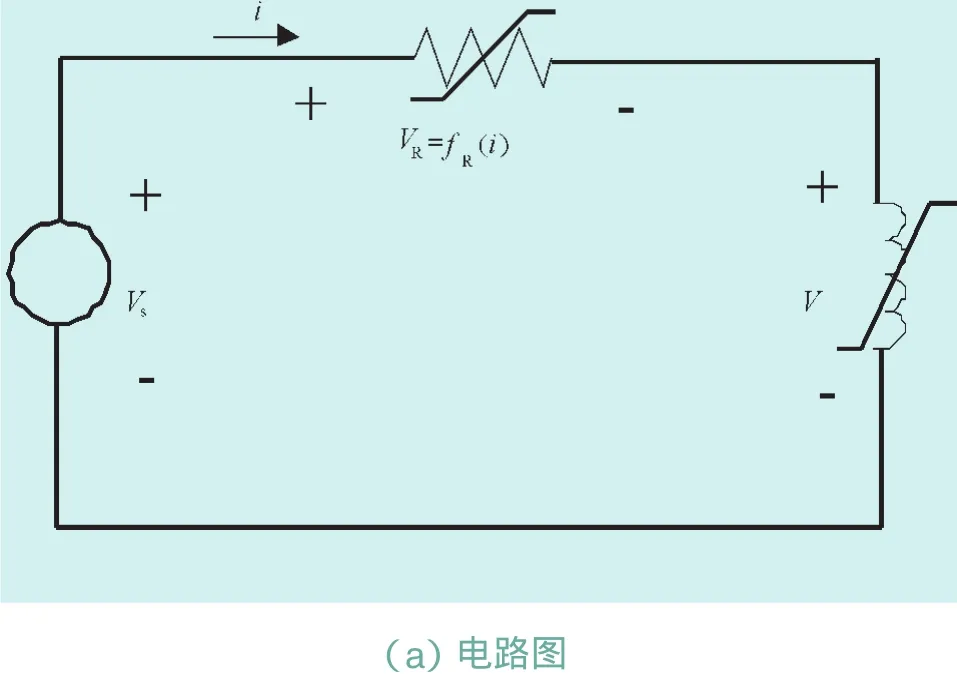
图5 非线性电流控制的电阻和电感电路图和它的线性伴随电路

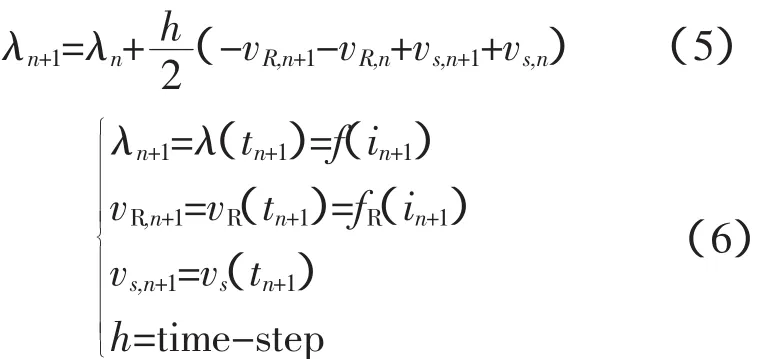
这里下标表示时间步序，步序n是已经完成的一步，步序n+1是下一步。

应当指出，λn+1和vR,n+1分别是在时刻tn+1的近似值λ和vR。

方程式（5）是一般意义的隐式非线性方程，它可以通过牛顿－拉夫逊的方法求解。

令

由牛顿－拉夫逊法得，

这里

这里上标是牛顿－拉夫逊迭代步序，迭代步序j被看作是完成的一步，迭代步序j+1是下一步。

方程式（9）、（10）定义了雅可比函数，增量电感和增量电阻，它们分别是在时间步序（n+1）和牛顿－拉夫逊迭代步序（j+1）处定义的函数。

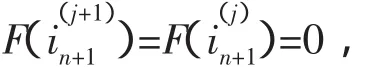
也即

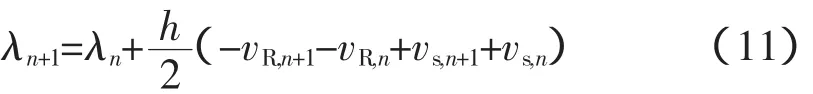
这里

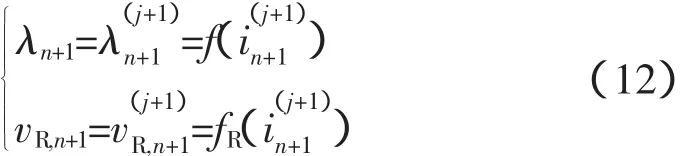
因此式（12）是视在电感和视在电阻，它们决定了最终的解。电感增量的倒数（d i/dλ）或电纳增量的倒数（d i/d v）用于求解节点电压，视在电感的倒数（i/λ）或视在电纳的倒数（i/v）用于求解非线性元件支路电流。然而当用牛顿－拉夫逊方法求解非线性电路时，增量电感和电阻也参与迭代。这表明，当迭代收敛时，视在电感和视在电阻决定了精度。增量电感和增量电阻则影响牛顿－拉夫逊法的迭代次数，但不会影响精度[6]。

3 算例证明

新算法有2个循环迭代，时间步序n的迭代和牛顿－拉夫逊步序j的迭代。新模型中假非线性元件Type-96－99不需要进行j迭代，不需要再次三角因子分解；真非线性元件需要2个迭代，j迭代一般2到3次即可以收敛，三角因子分解中，需要修改和非线性元件有关的部分元素。

非线性元件二极管的伏安特性如图6所示。其中v1=-0.5，v2=0，v3=0.6，v4=0.9。v1至v2段简化为直线，斜率为k1=（i2-i1）/（v2-v1），v3至v4段亦简化为直线，斜率为k2=（i4-i3）/（v4-v3），EMTP中非线性元件一般都是这样线性化处理的，如ZnO避雷器的低电压段。

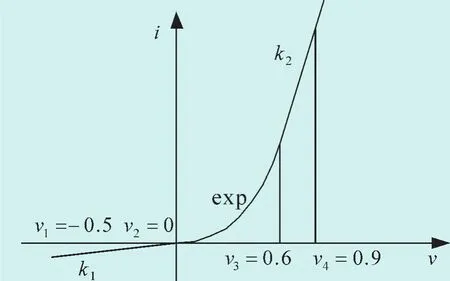
图6 非线性元件二极管的伏安特性

只有v2至v3段有解析表达式，iD=Is（eVD/VT-1），所以称二极管为非线性元件。它是一个电压控制型的非线性元件。

上式中Is=10-15A，vT=0.025 V，非线性电阻为

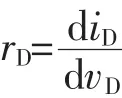
图7电路用来证明本算法的正确性。非线性元件二极管做三角形连接，这在EMTP中是不运行的。在EMTP中3个三角形连接的TYPE－96或3个三角形连接的TYPE－93电路都是不能运行的。图8（a）中，Ra，Rb，Rc为线性电阻；La，Lb，Lc为线性电感；Da，Db，Dc为非线性二极管。它的伴随电路如图8（b）所示。

用节点电压法求各节点电压[I]=[Y][U]

其中Y为节点导纳矩阵，

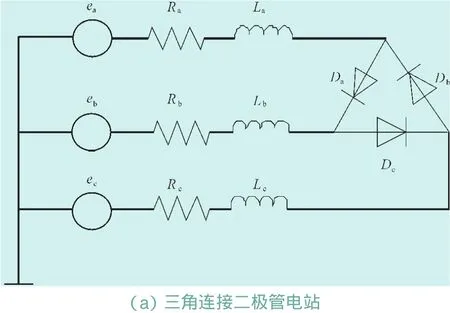
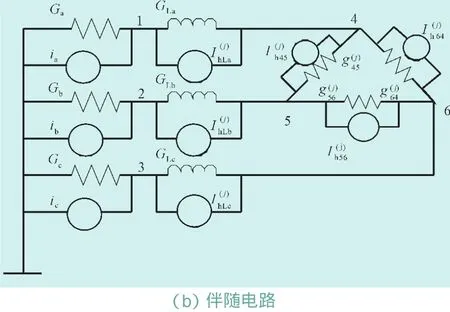
图7 三角连接二极管电路及其伴随电路

运行结果如图8所示。电源电压ea，eb，ec和节点va，vb，vc为正弦波电压，负载节点电压v4，v5，v6为交替导通的正向电压。电源电流iLa，iLb，iLc在2～3个周波的暂态后变为正弦波电流。负载二极管电流i45，i56，i64为正向导通电流，电流值大于0，电流交替达到最大值。

图8 三角形连接二极管电路的运行波形

结果表明牛顿-拉夫逊法非线性元件模型算法是正确的。

运行结果还表明，牛顿-拉夫逊法非线性元件模型具有良好的稳定性。在二极管的非线性特性下，没有出现数值振荡。

4 结语

运用本算法的非线性元件模型，可以将非线性元件模型和线性元件模型直接组成导纳矩阵，这一点类似于分段线性化模型，因此可以适用任意接线的和任意数量的非线性元件，即任意拓扑结构。这种算法的缺点是，因非线性参数变化而需要重新三角分解，因而增加的运算量比补偿法要多。若非线性元件采用分段线性化的方法，本算法不会增加任何运算量，因为同一段上每次n迭代的导纳矩阵不变。因此本算法适用于比较复杂的非线性元件电路，这需要进一步的研究探讨。

[1]Dommel H W.Electromagnetic Transients Program Reference Manual（EMTP Theory Book）[M].BPA,Portland,Oregon,USA.,August 1986.

[2]Watson N R，Jos Arrillaga.Power Systems Electromagnetic Transients Simulation[M].The Institution of Electrical Engine ers,London,United Kindom,2003.

[3]Christos Mademlis.Compensation of Magnetic Saturation in Maximum Torque to Current Vector Controlled Synchronous Reluctance Motor Drives[J].IEEE Trans.Energy Conversion,2003,18（3）：379-385.

[4]Essah D N，Sudhoff S D.An Improved Analytical Model for the Switched Reluctance Motor[J].IEEE Trans.Energy Conversion,2003,18（3）：349-356.

[5]Perkins B K,Marti J R,Dommel H W.Nonlinear Elements in the EMTP:Steady-state Initialization[J].IEEE Trans.Power Syst.,1995,10（2）：593-601.

[6]Canadian /American EMTP User Group Alternative Transients Program（ATP）Rule Book[M].1987-1992.