基于神经网络的KR脱硫控制工艺模型的研究
2010-05-10但斌斌李具中王雪冬邓品团
但斌斌,马 乾,李具中,王雪冬,邓品团
(1. 武汉科技大学 机械自动化学院,武汉 430081;2. 武钢钢铁(集团)公司,武汉 430083)
0 引言
随着钢铁市场竞争日趋激烈,用户对钢材品种和质量提出了更高的要求[1]。铁水脱硫处理是钢铁联合企业通常用以提高产品质量、开发生产高附加值产品的重要技术手段[2]。目前,以KR法为代表的机械搅拌脱硫法和喷吹脱硫法,作为两种主要的铁水脱硫手段,在我国一些转炉炼钢厂得到广泛地应用。提高脱硫指标与降低脱硫剂浪费成为脱硫生产过程中的两个主要的目标。在这种形式下,建立脱硫工艺过程参数的智能预报系统对脱硫生产进行指导,对于提高脱硫效率和提高脱硫生产的自动化水平,降低脱硫剂浪费,具有重要的实际意义和理论参考价值。
某钢厂KR脱硫系统投产以来,脱硫关键控制参数的选择都是由现场操作工人依据经验手工计算和设定,主观性强,产生的误差大,无法保证脱硫的稳定与精度。铁水脱硫过程是一个非常复杂的多元非线性反应过程。必须建立一个能够无限逼近于这一严重非线性多输入多输出系统的智能控制模型来替代操作工人的经验。这种非线性问题可以采用人工神经网络来解决。
1 神经网络
1.1 BP神经网络
神经网络是在现代神经生物学和认知科学对人类信息处理研究成果的基础上提出的,它具有良好的容错性、层次性、可塑性、自适应性、联想记忆和并行处理能力[3]。BP(Back-Propagation)神经网络是目前应用最广泛的一种前向神经网络,80%~90%的人工神经网络模型都是采用BP网络或它的变化形式。其学习规则是通过反向传播误差信号(样本输出与网络输出之差)并按原联接通路反向计算,由梯度下降法调整各层神经元的权值和阈值,使误差的平方和最小[4]。BP神经网络的网络结构如图1所示。
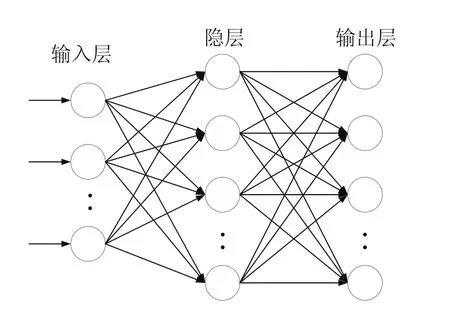
图1 基于BP算法的神经元网络的结构
标准的BP算法采用梯度下降法,虽然算法简单,容易实现,但其收敛速度慢且易陷入局部极小。而铁水脱硫对实时性要求较高,显然标准的BP算法不能满足需要。常用的改进方法主要分两类,一类是采用启发式的学习方法,如动量法、自适应调整学习速率法,来提高算法的可靠性和学习速度,另一类则采用更有效的数值优化方法,如L-M(Levenberg-Marquardt)算法[5]。
1.2 L-M算法及其实验结果
L-M算法实质上就是最速下降法和高斯-牛顿法的一个折中,其特点是利用最速下降法保证收敛这一特性,同时提供牛顿法收敛速度。实践证明,采用L-M算法可以较原来的最速下降法提高收敛速度几十倍甚至上百倍。
构建一个网络结构为5-6-3的神经网络,隐层和输出层的传递函数分别为对数-S形函数和正线性函数,以脱硫剂重量作为训练和预测对象,以L-M算法作为训练方法,以2005年1月至3月的记录作为训练样本集,并以2月至5月的记录验证网络性能。该实验重复三次,其结果如表1所示。

表1 L-M算法实验结果
此外,该算法对其他两个参数的预测结果亦不尽如人意。根据实验结果可以发现,训练后的神经网络系统出现了过拟合(Overfitting)现象,即对训练样本有较好的逼近结果,而对训练样本之外的数据则产生较大的误差。由此可见,直接使用L-M算法不适合作为KR脱硫系统的基本算法。
1.3 贝叶斯正则化
对于上述问题,可以通过减少神经网络的参数数量以缩小网络规模,促使神经网络没有机会出现过拟合条件,该方法称为正则化(regularization)方法[6]。为了自适应优化正则化方法的各参数,采用了贝叶斯理论;为了提高速度,采用了L-M算法。通过上述改进的BP神经网络,即贝叶斯正则化(Bayesian Regularization)BP神经网络。
一般的神经网络训练的性能指数为:

而贝叶斯正则化是在原来基础上加上一项网络权值的平方和,其公式如下所示。

其中α与β为性能指数的正则化系数,ED即为网络权值的平方和通过在网络训练中确定合适的α与β,在确保匹配精度的前提下,获得了良好的泛化能力。
2 控制模型的建立与测试
2.1 参数的确定
BP神经网络系统是对实际系统的数学描述,其输入/输出是由问题的外部描述决定的。根据查阅的资料以及实际情况,确定了5个输入参数为:铁水的质量、铁水的温度、铁水的含硫量、搅拌头的使用等级、铁罐的使用等级,3个输出参数为:加入脱硫剂的质量、搅拌时间和搅拌速度。
2.2 网络结构的确定
研究已表明,两层网络在其隐层中使用S形传输函数,在输出层使用线性传输函数,就几乎可以以任意精度逼近任何感兴趣的函数,只要隐层有足够的单元可用;此外,在用神经网络建模时,要用足以表示训练集的最简单的网络,即只要有一个更小的网络能工作,就不要使用更大的网络[7]。因此,本模型首先选择两层网络作为其结构,如果不能满足要求,再考虑增加隐层。
由上节内容可知,网络输入、输出层单元个数分别为5和3;对于隐层单元个数,可以通过对网络进行训练时ED、EW及网络有效参数ɣ的取值来确定,其中γ通过公式(3)进行计算。

上式中N表示网络权值的总个数,α、H分别表示神经网络性能指数在其最小点时的正则化系数和赫森矩阵。首先给隐层单元个数M一个较小的值(不妨使其等于2),然后不断增加其值,并对网络进行训练;如果从某个M开始,随着它的增大,ED、EW、ɣ的值基本不变,那么这个M就可以作为隐层节点数目。
表2是对网络隐层节点数目的选取和训练参数。根据上述内容,由表2可以看出,网络隐层节点可以选6。
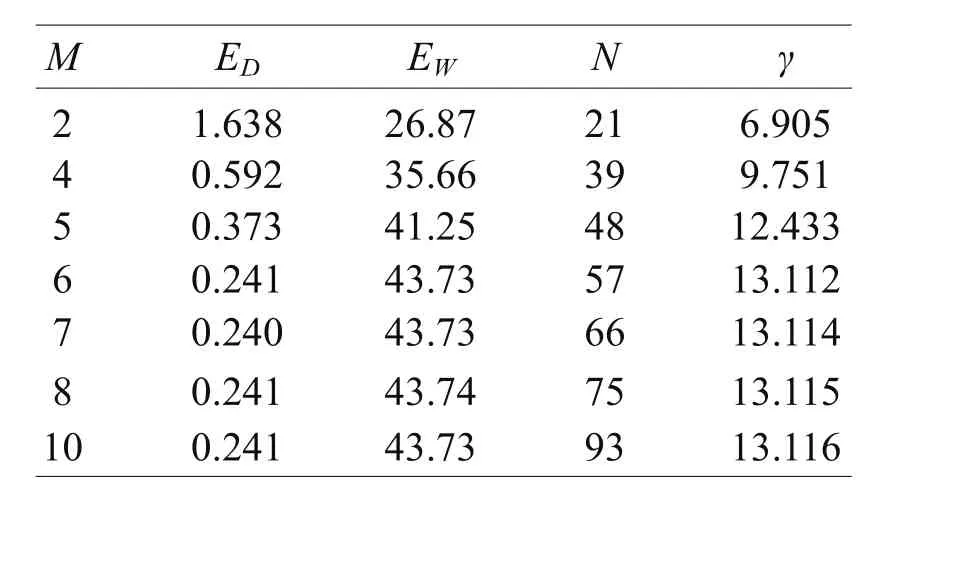
表2 脱硫模型网络隐层节点的选取和训练参数
综上所述,确定KR脱硫控制模型选用贝叶斯正则化BP算法,网络结构为5-6-3,隐层、输出层传输函数分别为对数-S形函数和正线性函数。
2.3 控制模型的测试
仍然以2005年1月至3月的记录作为训练样本集,并以2月至5月的记录验证新模型的网络性能,得到如表3所示的结果。虽然网络对于训练样本的误差增加,但对其他数据的误差比直接使用L-M算法有较大幅度的减小,其综合性能明显优于前一个模型。经过多次测试,终点脱硫命中率大于90%。

表3 贝叶斯正则化BP算法实验结果
3 结论
本系统经过一段时间的开发研制,已于2005年1月将软件系统投入生产现场试运行。通过试运行,离线系统运行正常,预测数据准确、可靠,统计分析迅速、准确,基本达到设计要求。通过优化控制工艺模型,规范了操作工人主观误差,提高了脱硫效率。
[1] 王雪冬,李凤喜,陈清泉,等.KR脱硫技术的应用与进步[J].炼钢,2004,20(4):24-25.
[2] 李凤喜,李具中,萧忠敏,等. 武钢二炼钢KR铁水脱硫生产实践[J].炼钢, 2005,21(5):1-4,53.
[3] 张莲,余成波,刘述喜,等. 基于神经网络的异步电动机信息融合故障诊断系统[J].微电机,2007,23(8-1):1-3.
[4] 杨升,胡寿根,王宗龙.基于BP人工神经网络的磨料水射流切割深度模型[J].上海理工大学学报,2008,30(6):528-530.
[5] 凤德伟,张忠能,凌君逸.基于神经网络的短期销售预测[J].计算机工程,2004,30:363-364,390.
[6] 李红连.小波-神经网络在GPS/DR组合导航中的应用研究[D].西南交通大学,2006.
[7] Martin T. Hagan等. 戴葵,等译.神经网络设计[M].北京:机械工业出版社,2002.
