基于异速增长模型的土地利用变化驱动因子分析——以湘潭市为例

王昭生，潘爱民，肖志坤，黄 凯，王 芳，2，3，陶建军，全 斌

(1.湖南科技大学，湖南 湘潭411201;2.北京师范大学，北京 100875;3.中国科学院 遥感应用研究所，遥感科学国家重点实验室，北京100101)

人类社会的各种生产活动引起土地资源系统中各个资源要素以及各要素之间的关系随时间推移[1]，在地理分布、系统结构上发生深刻变化，使土地资源系统的增熵(Δ S＞0)变小，即人类活动为该系统注入了太多的负熵。同时，由于耕地面积、森林植被覆盖度的减少以及土地利用结构的急剧变化等因素，使得生物多样性受到严重威胁、土地资源系统和生态系统的自身调节能力大大弱化。这更加激化了土地进化与退化间的矛盾，陆地表面正经历着深刻的变化。土地利用作为地球表层最突出的景观标志[2]，自然成为其变化突显的载体。其变化痕迹是自然环境系统与人文社会系统矛盾调和的产物。追踪研究这种变化痕迹，有益于提出为建立人类的生产和经济活动与自然生态系统相互协调，并可持续发展的方法或手段。从湘潭市土地利用变化[3](热点)过程中探寻湘潭市“两型社会”(“资源节约型”和“环境友好型”社会)建设的基点，是非常有必要的。

目前，土地利用/土地覆被变化(LUCC)研究方法主要有两种:一是利用土地利用变化的因素模型示踪土地利用变化的机制[4-6];二是将土地利用的时空演变过程纳入城市用地扩展的细胞自动相互作用模式来揭示土地利用/土地覆被变化的机理[6-9]。此外，3S技术与土地科学时空演变模型的融合，使土地利用变化研究走进了空间尺度，从土地利用的宏观变化现象探究土地利用/土地覆被变化的机理。例如全斌[10]、刘锬[11]、鲍振洪[12]等对长株潭地区土地利用变化进行了研究。但本研究把主要的研究方法融合起来，以湘潭市土地利用变化为例，从LUCC的因果关系去探讨、预测土地资源系统变化的趋势，即多重驱动因素与结果变化的研究，以此去理清人地关系，欲检验湘潭市土地资源系统的稳定性，同时强调土地资源系统中某些驱动因子间存在的此消彼长的关系，诸如土地资源与人口数量之间的关系，进而监测土地集约利用状况，为建设好“资源节约型”社会做理论参考。

1891年，Snell提出了异速增长定律(The law of allometric growth)，Naroll和 Bertalanffy[13-15]将异速增长定律引入地理学领域，应用于城市地理，研究城市的局部变化与整体变化的关系。异速生长分析在城市地理学有着重要的应用，主要用于探讨城市体系各主要要素之间或要素与整体之间的标度特征[16]，在城市系统发展预测[17]和因果解释、系统分析方面[18]也有着重要的应用价值。Beckmann和周一星[13]指出了异速增长模型是模拟城市开放系统中变化的一种流行随机模式。1973年，Bradford D.和Kelejian H.基于异速增长模型提出B-K模型[19]度量郊区化的城市人口-城区面积。陈彦光[20]和刘继生[17]揭示了城市人口-城区面积的异速生长关系。吴金华[21]指出用这种关系中的异速生长系数变化动态监测城市土地利用集约度的变化，这有助于不断提高城市用地规模的经济效益。经实证研究了西安人-地关系[21]和河南省城乡-人口异速增长的分数维性质[22]以及山东省城市人口与城区面积异速增长的关系[17]，表明异速增长模型可以很好地描述一系统中某一部分的相对增长率同整个系统或系统的另一部分的相对增长率。作者尝试用异速增长法则阐释湖南省湘潭市土地资源系统中的人地关系，从微观角度揭示各驱动因子间存在的相互关系，寻求自然环境系统与人文社会系统协调发展的基点，即人地系统的动态平衡点，藉此能够监测湘潭市土地资源系统的自组织能力的大小(稳定性)，找到解决土地进化与退化矛盾和土地利用类型间在时空上合理转化矛盾的方法或手段，为建设好长株潭“两型社会”提供理论参考。

1 研究区概况和数据来源

1.1 研究区概况

湘潭市位于东经 111°58′-113°05′，北纬 27°21′-28°06′，地处湖南省中部偏东地区 ，湘江下游 ，东接株洲，南靠衡阳，西邻娄底，北界长沙，距省会长沙50 km，与长沙、株洲共同构成湖南“新三角”城市群，构成湖南省政治、经济、文化最发达的“金三角”地区，是广大内陆地区通往广州、上海等沿海地区的重要通道之一。辖区面积5 019万km2，下辖岳塘、雨湖2市辖区、湘潭1县、湘乡、韶山2县级市，总人口292.70万。

1.2 数据来源

所用数据来源于湘潭市国土局、统计局、房产局，所需数据有湘潭市1999-2008年10 a间的人口数量、GDP、耕地面积、城镇住宅土地面积(利用住宅面积，依据湘潭市房产局提供的建筑容积率推算所得)。

2 研究理论与方法

2.1 异速增长模型

异速增长定律的生物学含义是指“一个器官的相对增长率与整个生物体的相对增长率具有恒定的比值”。类比于生物现象，它描述的是一个系统中某一部分的相对增长率同整个系统或系统的另一部分的相对增长率之比保持不变，即为一个固定常数的一种相对增长关系。用数学表达式来描述即为:

对式(1)乘以dt，再两边求积分得，

或

式中:c——常数，也叫比例系数，且 c＞0;t——时间;a——异速增长系数。式(2)，(3)称为异速增长等式(allometric equation)。

2.2 异速增长模型性质

性质(Ⅰ)异速增长模型是一种线性关系。由(2)式可推得，异速增长模型中的两个变量在双对数坐标系中呈显一定的线性关系，或重合，或平行，即变量的变化用直线拟合具有良好的效果。

性质(Ⅱ)异速增长模型具有分维性，有分数维性质。依据指数函数和幂函数的性质，可知式(3)存在3种变化，当a=1时，变量之间呈线性关系;当0＜a＜1或a＞1时，变量的变化现象具有凹凸性。如图1所示，异速增长模型具有分维性，有分数维性质。据此，可以把异速增长模型分为正异速增长模型(a＞1)、负异速增长模型(0＜a＜1)、等异速增长模型(a=1)。这种分维性可以很好地刻画一个系统中某一部分同整个系统或系统的另一部分的相对增长关系。

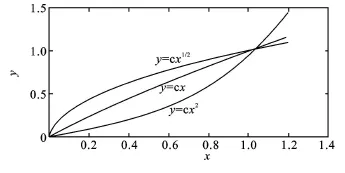
图1 异速增长模型的分维性示意图

为了更精细地刻画这种相对增长关系，本研究参考文献中异速增长系数临界值的选取标准[16，23，24]，分维临界值取0.9，如表1所示。

表1 异速增长模型类别

性质(Ⅲ)异速增长规律在稳定的系统中普遍存在着，它可以粗略表征一个系统的稳定性。异速增长规律发现于哺乳动物体的生长过程中，而动物体本身就具有很强的自组织能力，是一个比较稳定的系统。即稳定的系统中存在着类似这种生物现象的规律。如果一个系统中发现某一部分的相对增长率同整个系统或系统的另一部分的相对增长率之比保持不变，即存在异速增长规律，并且存在较普遍，那么利用它就可以粗略地反证系统的稳定性。土地资源系统中各要素在随时间序列变化的过程中若大量存在这种变化现象，那么它的稳定性就可以粗略地得以印证。

2.3 研究方法

首先，依据异速增长模型，欲设定四种分析情景，具体如表2所示。其次，对四组驱动因子做相关分析，检核设定的分析情景是否有效。若因子之间的相关度显著，说明分析情景有效，有利于探究土地资源系统中驱动因子间的相互关系。最后，利用异速增长模型，探究湘潭市土地利用变化驱动因子间的相互关系和土地资源系统的稳定性。

表2 分析情景

3 结果与分析

利用SPSS软件对湘潭市土地利用变化变化驱动因子(四组)做相关关系分析，结果如表 3所示，1999-2008年间湘潭市人口数量和耕地面积呈负相关，其相关系数r=-0.719**，相关性较显著;GDP和耕地面积呈高度负相关，其相关系数 r=-0.861**，相关性十分显著;GDP和城镇住宅土地面积的相关系数r=0.977**，呈高度的正相关;耕地面积和城镇住宅土地面积的相关系数r=-0.806**，呈比较显著负相关。由此可见，四组因子都呈显高度相关，四种分析情景有效，同时表明湘潭市土地资源系统中此消彼长的变化显存，所预选的驱动因子间的相互关系也比较显著，可以利用异速增长模型来更好地探究湘潭市土地利用变化驱动因子间的相互关系。

表3 驱动因子相关分析

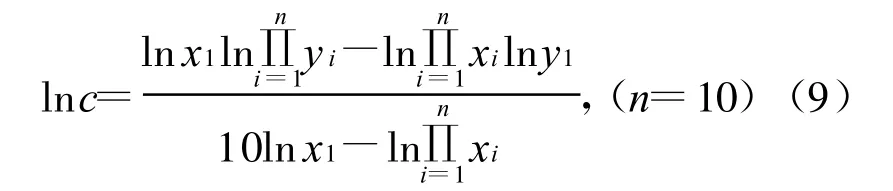
将 x1，y1修正为10 a数据的平均值，有

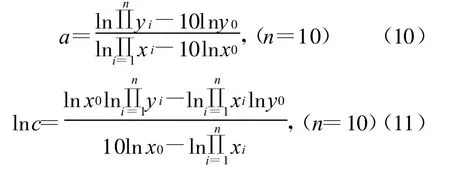
其中x0，y0指平均值。将四组数据进行无量纲化处理(采用极大值标准化法进行标准化处理，即选取同类值中最大值作为标准值)后，再同时扩大100倍(便于数据分析，但又不会影响数据的变化趋势)，然后分别代入式(10)、(11)，求得四种分析情景下的异速增长模型如表4所示。

表4 异速增长模型

将A、B、C、D四种分析情景下的理论值与真实值表达于双对数坐标图2中，人口和耕地变化图像拟合较好;GDP与城镇住宅土地面积图像变化趋势相似;C中GDP的变化与耕地面积的变化趋势有差异;D中城镇住宅土地面积和耕地面积的变化趋势在时间序列上表现一定的异速变化。A、C、D拟合较好，但B表现不理想，其原因是湘潭市从1999-2008年城镇化速度不均一，区域间城镇化发展不平衡，GDP增长与土地要素属性变化不协调所致，具体体现在城镇住宅土地面积的变化和房地产开发固定投资的不均一，如图3-4。

A组:人口和耕地的变化趋势在双对数坐标中趋于一致，表现出良好的拟合效果，说明A属于典型的异速增长现象。另外，异速增长模型模拟的结果显示，耕地面积的实际值与理论值的拟合效果较好，依据异速增长判断标准(表1)，A属于典型的负异速增长，耕地面积总量随人口规模的不断扩大，其数量上表现出微弱的增多，但人均耕地面积减少。若人口增长1%，则耕地面积增加0.101倍，人均耕地面积减少0.000 1倍。

图2 异速增长模型模拟结果

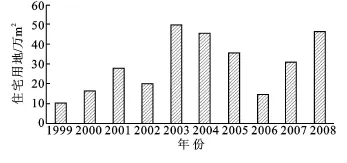
图3 湘潭市城镇住宅土地面积

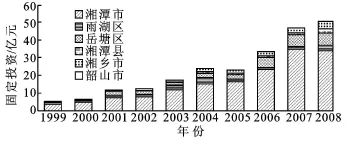
图4 湘潭市房地产开发固定投资分布

B组:GDP和城镇住宅土地面积的变化趋势在双对数坐标中趋于一致，拟合效果较差，异速增长模型还不适合描述当前湘潭市GDP和城镇住宅土地面积的变化情况。模拟结果显示，Sz和sz的拟合效果虽比较差，但其变化趋势却一致，说明城镇住宅土地面积的变化受GDP的影响。另外，不难看出在时间序列上，GDP(实际值)增长的同时，城镇住宅土地面积(实际值)也表现出增长的态势。由此可知GDP的变化对城镇住宅土地面积的变化有一定的影响。sz＞Sz表明这种影响不能用简单的幂函数来描述，它会夸大GDP对城镇住宅土地面积变化的贡献率。这种夸大的效果类似于图像在二维坐标系中的平移。

C组:GDP和耕地面积的变化趋势在双对数坐标中趋向于平行，其拟合效果较差，由此可见这种现象不适合用异速增长模型来表达，但其模型处理结果sg与Sg的拟合效果良好，说明两者的增长是按照一定的比例变化的，从整体来看，是负异速增长。但局部的不规则变化如图2湘潭市从2005-2008年间，GDP增速变大，但耕地面积近乎静止，这反映出耕地的集约度增大了，耕作技术有了显著提高。GDP对耕地的变化有一定的贡献率，这种贡献不能用简单的幂函数来表达，它是幂函数和其他函数的复合表达，但可以用GDP变化来预测湘潭市耕地的变化情况。

D组:耕地面积和城镇住宅面积的变化趋势差异较大，如同线性函数和幂函数的变化差异。但依据异速增长模型模拟后，耕地面积的变化趋势同初始耕地面积变化趋势一致，拟合较好，说明混杂有不规则变化的负异速增长。

从B、C、D三组分析结果来看，虽然湘潭市城镇住宅土地面积、GDP和耕地面积两两之间具有高度的相关性，但用异速增长模型来定量详细描述它们的相互关系时表现为“不适应”和模拟结果“出奇”(即理论值与实际值的拟合效果良好)现象。这“三个不适应”表明土地资源系统不稳定，系统的自身调节能力不强，各要素间不能更好的协调发展。另外，异速增长模型不能很好地定量描述湘潭市土地资源系统中的相对增长关系，它存在一定的局限性。模拟结果出奇表明湘潭市的城市化进程正处于完善系统结构功能的阶段，同时也表明湘潭市土地资源的集约利用有待加强，具体表现为城镇住宅土地的单位产值不高。

4 结论与讨论

4.1 结论

(1)1999-2008年10 a间湘潭市人口数量和耕地面积变化表现为典型的负异速增长现象。人口规模扩大时，耕地面积会微弱增加，但人均耕地面积不断减少，若人口增长1%，则耕地面积增加0.101倍，人均耕地面积减少0.000 1倍。

(2)湘潭市GDP与耕地和城镇住宅土地面积彼此间不存在异速增长现象。虽然其相关系数r≥︱0.806**︱，但只能虚弱反映GDP会影响耕地和城镇住宅土地面积的变化。

(3)异速增长模型用于详细描述湘潭市GDP和耕地与城镇住宅土地面积相互关系时，表现出“三个不适应”，表明土地资源系统结构功能还不完善，系统不稳定，土地资源的集约利用度不高。

4.2 讨论

本研究与以往的土地利用变化研究的方法有所不同:①不是从土地利用变化的宏观表象进行究根问底的，而是直接从引起土地利用变化的动因着手，研究土地利用变化;②从系统论观点出发，强调因子间潜在的相互关系，揭示土地资源系统的稳定性。

鉴于湘潭市土地利用变化过程中存在的问题，试提出一些建议:(1)湘潭市“两型社会”建设过程中，要协调好人-地关系，特别使人口变化时相与耕地的承载力相适应，这有益于确保粮食安全，有益于保证耕地的生产功能不退化;(2)在资源节约、环保的前提下，可以利用先进的生产技术，加强土地的集约利用，特别要提高城镇建设用地的容积率，以此减缓耕地向建设用地的转换速度;(3)要注重培育低碳经济增长点，使得自然与人文社会环境协调发展，这有助于完善土地资源系统的结构功能，增强系统的稳定性。

[1] 马蔼乃.地理信息系统工程[M].北京:高等教育出版社，2006.

[2] 全斌.黄土高原六盘山区土地利用变化及生态农业模式比较研究[D].陕西杨陵:中国科学院教育部水土保持与生态环境研究中心，2007.

[3] 全斌.中国西北与东南土地利用变化及比较[M].北京:中国环境科学出版社，2010:4-10.

[4] The National Institute for Environmental Studies(NIES).Japan:land use for global environmental conservation project[R].Lu/GEC，1995.

[5] 李平，李秀彬，刘学军.我国现阶段土地利用变化驱动力的宏观分析[J].地理研究，2001，20(2):129-138.

[6] 梁进社，王旻.城市用地与人口的异速增长和相关经验研究[J].地理科学，2002，22(6):649-654.

[7] Geoffrey G R，Fole S.City life:a study of cellular automata in urban dynamics[M]//Fischer M ，Henk J S，David U.Spatial analytical perspective on GIS.London:Taylor&Francis，1996:213-228.

[8] Wu Fulong.A linguistic cellular automata simulation approach for sustainable land development in a fast growing region[J].Computer，Environment and Urban System ，1996，20(6):367-387.

[9] 帅江平.供求平衡状态下的城市自组织过程[J].地理学报，1996，51(4):374-383.

[10] 全斌，李吟，陶建军，等.基于GIS和遥感的土地利用变化及区域比较研究[J].湖南科技大学学报:自然科学版，2010，25(1):81-86.

[11] 刘锬，袁开国，全斌.湘潭市城市化空间格局及土地利用/覆被变化分析[J].安徽农业科学，2009，37(12):5599-5601，5613.

[12] 鲍振洪，李朝奎，郑拴宁，等.城市土地利用潜力分析及其3D可视化辅助管理:以湘潭市为例[J].江西农业学报，2009，21(4):151-154.

[13] 周一星.城市地理学[M].北京:商务印书馆，1995:263-274.

[14] Naroll R S，Bertalanffy L.The principle of allometry in biology and social sciences[J].General Systems Year-book ，1956 ，1:76-89.

[15] 陈彦光.Beckmann城市体系异速生长模型的理论基础与实证分析[J].科技通报，2002，18(5):360-367.

[16] Lee Y.An allometrie analysis of the US urban system:1960-1980[J].Environment&Plnaning A，1989，21(4):463-476.

[17] 刘继生，陈彦光.山东省城市人口-城区面积的异速生长特征探讨[J].地理科学，2005，25(2):135-141.

[18] 陈彦光，刘继生.城市系统的异速生长关系与位序一规模法则:对Steindl模型的修正与发展[J].地理科学，2001，21(4):412-416.

[19] Bradford D，Kelejian H.An econometric model of the flight to the suburbs[J].Journal of Political Economy，1973，81:566-589.

[20] 陈彦光，余斌.异速生长定律与城市郊区化的分维刻画[J].华中师范大学学报:自然科学版，2004，38(3):370-378.

[21] 吴金华，吴国栋.基于城市人口-城区面积异速生长关系的西安市城市化水平测算模型研究[J].国土资源科技管理，2008，25(1):92-95.

[22] 陈彦光，靳军，余国忠.河南省城市化进程的异速生长分析[J].信阳师范学院学报:自然科学版，1999，12(3):321-325.

[23] Lora A H.Allometric Laws and Prediction in Estuarine and Coastal Ecology[J].Perspectives in Estuarine and Coastal Science，2006 ，29(2):340-344.

[24] 石元安.80年代以来我国城市人口与用地的异速增长分析[J].城市问题，1996(1):8-12.