基于GIS的黄土高原气象要素空间插值方法*

孟庆香，刘国彬，杨勤科

(1.河南农业大学资源与环境学院，郑州450002;2.中国科学院水利部水土保持研究所陕西杨陵712100)

黄土高原位于中国西北部，包括山西、甘肃、宁夏全部和陕西、河南、内蒙、青海部分地区，共计7省区287个县，总面积 62.4万 km2。温度、降水等气候因素是黄土高原农牧业发展和生态环境恶化的重要制约因子，在气候变化和人类活动的共同作用下，该区成为世界上水土流失较严重的地区之一。因此，研究气候空间分布特征成为促进农牧业发展和保护生态环境的必须，而获取精确气候数据的方法之一就是建立高密度的气象站点。然而，由于经济、技术等原因，气象站点是有限的，而定点观测到的数据大多不能直接用于其他地点，更不能代替某一较大面积上的平均值。在实际工作中，研究人员将地统计学方法与地理信息系统相结合，通过对已知站点气象数据进行空间插值，实现由点数据到面数据的转化，生成研究区气象要素的空间分布图，则是一种有效的解决方法。目前，国外对此已进行了大量研究[1-5]，而国内研究还较少。因此，本研究利用黄土高原已知的102个气象站点气候资料，进行区域年均温的空间插值，探讨不同插值方法对研究黄土高原气候空间分布特征的影响，对黄土高原环境变化研究以及环境治理也有十分重要的指导作用。

1 数据与方法

1.1 数据基础

气象数据来源于国家气象局102个气象站点1950-2000年观测值[6]。102个气象站点的空间分布见图1。以气象站点的地理坐标和海拔高程作为自变量，由日降水量计算的多年年均降水量和由月均温计算的多年年均气温用于插值。同时，以1∶50万黄土高原行政区图和1∶25万黄土高原数字高程图(DEM)为参照。

图1 参与空间插值的102个气象站点分布图

1.2 软件工具

软件工具采用美国环境系统研究所(ERSI)的GIS桌面平台系统ArcGIS 8.3以及目前常用的微软电子表格工具Excel 2003。在ArcGIS 8.3的三大模块中，ArcMap主要用于空间数据显示、编辑、查询、检索、统计报表生成、空间分析和高级制图等;ArcCatalog主要用于空间数据的浏览;ArcToolbox主要用于空间数据格式转换、叠加处理、缓冲区生成和坐标转换等[7]。电子表格工具Excel 2003主要用于原始数据的输入和数据的简单计算等。

1.3 数据处理转换

上述研究成果多以微软电子表格xls文件形式保存，由于目前ARCGIS尚不能很好地支持xls文件格式(必须加载 EXCEL_TOOLS工具才能实现)，因此首先把含有各气象站点编号、经纬度、海拔高程和年均降水量的.xls文件保存为.dbf格式，然后通过ArcMap中的转换工具将此文件生成黄土高原气象站点图。

为了与其他图件(如行政区图和DEM)进行叠加，上述数据均被统一到统一的坐标系和投影下。所采用的投影为等面积割圆锥投影(ALBERS)，中央经线为东经109.30°，双标准纬线分别为北纬36.30°和北纬 37.10°，所采用的椭球体为 KRASOVSKY椭球体。

1.4 研究方法

目前，用于气象要素空间插值的方法有很多，本研究主要采用反距离权重法、多项式插值法、径向基函数插值法和克里金等方法。这里主要介绍反距离加权插值法、克里金法和协克里金法。

1.4.1 反距离加权插值法(IDW) 该法是20世纪60年代末提出的方法。IDW实际是一种加权移动平均方法，将计算区域划分成若干矩形网格，每个网格的宽度和长度分别为Δx和Δ y，网格格点处的降水量xj可用其周围邻近的气象站实测资料按距离平方的倒数插值求得，即:

式中:xj——第 j个格点处插得的降水量;pi——第j个格点邻近的第i个气象站点的实测降水量;di——第j个格点到其周围邻近的第i个气象站点距离;m——第j个格点邻近的气象站点个数。反距离加权插值法的缺点是其计算值易受数据点集的影响，从而使计算结果常出现一种孤立点数据明显高于周围数据点的情况。

1.4.2 克里金方法(Kriging) 克里金方法是建立在地统计学基础上的一种插值方法，最早由法国地理学家Matheron和南非矿山工程师Krige提出[8]，并用于矿山勘探。克里金方法充分吸收了地理统计的思想，其原理是假设某种属性的空间变化既不是完全随机也不是完全确定。反之，空间变化可能包括三个影响因素:空间相关因素，代表区域变量的变化;偏移或结构，代表趋势;还有随机误差。偏移出现与否和对区域变量的解释导致了用于空间插值的不同克里金方法的出现，主要有简单克里金方法(Simple Kriging)和普通克里金方法(Ordinary Kriging)。简单克里金方法假设不存在偏移，关注与空间相关因素。普通克里金方法假设除了已知点之间的空间关系外，空间变量在z值上还有偏移或有结构因素，表现为一个趋势。总体而言，克里金方法认为，当空间变量的结构性成分确定后，剩余的差异变化属于同质变化，不同位置之间的差异仅是距离的函数，可以表示为

式中:z(x0)——x0处的估计值;z(xi)——xi处的观测值;λi——克里金权重系数;n——观测点个数。

1.4.3 引入高程信息的协克里金方法(Co-Kriging) Dirks等[3]发现，当站网密度较高时，普通克里金方法的插值效果与其他常用方法相比并无多大优势。Borga等[4]也曾得到同样的结论。但是，随着高程的增加，降水量有增加的趋势。Hevesi等[8]研究了年平均降水量与高程的相关性，得到了其相关系数达到0.75的结果。因此，本文采用协克里金方法，并将高程作为第二影响因素引入到对降水量的空间插值中来。对多个具有空间相关性的空间变量进行估计的克里金方法可以归类为协克里金方法。借助这类方法，可以利用几个空间变量之间的相关性，对其中的一个变量或多个变量进行空间估计，以提高估计的精度和合理性。虽然协克里金方法的基本原理早已为人们所熟知，但至今仍不经常使用，究其原因，主要在于其符号和算法比较复杂，交叉协方差函数和交叉变异函数的求取比较困难。

当研究区域内的第2类信息(如高程)随处可知且变化平稳时，可将这类信息作为第2类影响因素引入协克里金方法。考虑高程影响的协克里金估值方法可表示为

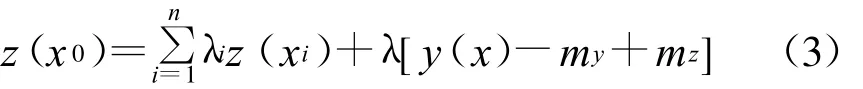
式中 :z(x0)，z(xi)，λi含义同式(2);y(x)— —x 点处的高程;my，mz——分别为高程和降水量的全局平均值;n——观测点个数。

与克里金方法一样，引入高程信息的协克里金方法也有简单克里金方法(Simple Kriging)和普通克里金方法(Ordinary Kriging)之分。

2 插值结果与分析

2.1 不同插值方法比较

本研究采用克里金(Kiging)和协克里金(Co-Kriging)方法进行插值(选用Spherical模型)，每种方法分别采用简单插值和普通插值。为了与常规插值方法进行比较，同时运用了反距离加权插值法(IDW)、全局多项式插值法(GPI)、局部多项式插值法(LPI)和径向基函数插值法(RBF)进行插值。运用Cross-Validation进行交叉验证，并对各参数进行修正，以期得到最好的插值结果[9-13]。

2.1.1 常规方法与地统计学方法的比较 将以上插值方法所得拟合值与实测值进行比较，计算误差均值(MEAN)和误差均方根(RMS)，结果见表1。一般来说，各种插值方法的MEAN和RMS总体最小者，具有较好的插值效果，尤其是RMS越小越好。从表1可知，对于降水量空间插值结果，误差均方根排序为普通克里金插值法＜局部多项式插值法＜径向基函数插值法＜普通协克里金插值法＜简单克里金插值法＜反距离加权插值法＜简单协克里金插值法＜全局多项式插值法;误差均值排序为普通协克里金插值法＜全局多项式插值法＜简单协克里金插值法＜普通克里金插值法＜反距离加权插值法＜径向基函数插值法＜简单克里金插值法＜局部多项式插值法。综合来看，普通克里金和普通协克里金效果较好，进一步选择插值方法，可以通过不同克里金插值的广义交叉验证得到。

同理，对于年均温空间插值，误差均方根以简单协克里金插值法最小，普通协克里金插值法次之;且简单协克里金插值法误差均值最小，普通协克里金插值法次之。局部多项式插值法的误差均值最大，径向基函数插值法的误差均值也大于普通协克里金和简单协克里金。综合来看，普通协克里金和简单协克里金效果较好，尤其是简单协克里金效果更好。从插值的MEAN和RMS总体最小看气候插值结果，无论是降水量还是年均温，地统计学方法均优于常规方法。

表1 基于102个气象站点不同插值方法检验比较的结果

2.1.2 不同克里金插值方法的比较 地统计学中通常采用以下5个指标评价其预测精度，即:预测误差的均值(MEAN)、预测误差的均方根(RMS)、平均预测标准差(ASE)、平均标准差(MS)和标准均方根预测误差(RMSS)。其中，前4个指标越小越好，主要是RMS越小越好，第5个指标越大越好。

表2 基于102个气象站点不同克里金插值方法检验比较的结果

通过广义交叉验证，从表2可以看出，对于年均温空间插值，从绝对值看，预测误差的均值排序为简单克里金插值法＞普通克里金插值法＞普通协克里金插值法＞简单协克里金插值法;预测误差的均方根排序为简单克里金＞普通克里金插值法＞普通协克里金插值法＞简单协克里金插值法;平均预测标准差排序为简单协克里金插值法＞简单克里金＞普通克里金插值法＞普通协克里金插值法;平均标准差排序为简单克里金＞普通克里金插值法＞普通协克里金插值法＞简单协克里金插值法;标准均方根预测误差排序为普通克里金插值法＞普通协克里金插值法＞简单克里金＞简单协克里金插值法。虽然，从标准均方根预测误差看，普通克里金插值法较好，从平均预测标准差看，普通协克里金插值法较好，但是，从预测误差的均值、预测误差的均方根和平均标准差看，简单协克里金插值法较好，尤其是简单协克里金插值法预测误差的均方根最小，综合5项指标，选用102个气象站点，对黄土高原年均温进行插值，简单协克里金插值法效果最好。其原因主要是简单协克里金法将海拔高程作为第二影响因素引入到对年均温的空间插值中来，利用地理位置、海拔高程和气温等空间变量的相关性，对温度进行空间估计，大大提高了插值精度和合理性。

从表2可以看出，对于降水量空间插值结果，普通克里金与普通协克里金相比，RMS和ASE小，虽然MEAN和MS略大，但是RMSS也略大，因此，普通克里金法是降水量空间插值的最佳方法。同理，简单协克里金法插值效果最好。

2.2 黄土高原气象要素的空间分布

2.2.1 黄土高原降水量空间插值结果分析 通过以上分析，降水量采用普通克里金方法进行空间插值效果最好。黄土高原降水量空间分析就是采用基于102个气象站点普通克里金方法插值实现点数据到面数据的转换。用黄土高原行政区划图对102个站点插值得到的栅格图进行截边，得到黄土高原降水量等值线图。黄土高原年均降水量的空间分布见附图1。

由附图1可知，黄土高原降水量偏少，多年平均降水量变化在117～721 mm。降水量分布存在明显的地区差异和年季变化。黄土高原降水量总体分布呈现西北低、东南高的态势，界限很明显。内蒙古的河套地区到宁夏银川一线的西北部分降水量不足200 mm，属于干旱地区，植被类型是草原化荒漠，植被稀疏。神木-靖边-会宁一线以北的大部分地区降水为200～400 mm，属于半干旱地区，其中，包头-盐池-同心一线以北为重半干旱区，以荒漠草原植被为主，以南属于轻半干旱区，植被类型为典型草原。但青海部分地区比较复杂，年均降水量为400～500 mm。区域内山西、河南以及西安-天水以北的陕甘地区降水量为400～600 mm，此线以南降水为600～800 mm，属于半湿润地区。400 mm不仅是半干旱-半湿润气候的分界线，亦是畜牧业区和农耕区的分界线，该线以北适于牧业生产，以南适于农业生产。

从降水量分布面积上看，在黄土高原，年均降水量小于200 mm的干旱地区占总面积的7.02%，年均降水量为200～400 mm的半干旱地区占总面积的35.46%，年均降水量为400～800 mm的半湿润地区占总面积的57.52%。其中，在半湿润地区，年均降水量400～600 mm占半湿润区面积的96.87%，年均降水量600～800 mm占3.13%。黄土高原半湿润和半干旱面积占整个区域面积的4/5以上，因此，黄土高原以半湿润-半干旱气候为主。

黄土高原天然降水量少，而年蒸散量多为700～1 000 mm，水分亏缺严重，不仅使农业生产受到限制，而且常常又与气候干旱互为因果关系，招致大风所导致的风蚀危害，使区域环境进一步恶化。

2.2.2 黄土高原年均温空间插值结果分析 通过分析，年均温空间插值采用简单协克里金方法效果最好。黄土高原年均温空间插值分析就是以高程为协变量的简单协克里金方法。用黄土高原行政区划图对102个站点插值得到的栅格图进行截边，得到黄土高原年均温等值线图(见附图2)。

黄土高原地区年均温变化在1.0～14.0℃，由附图2可知，黄土高原年均温总体分布呈现西北低、东南高的态势，界限很明显。青海省西宁-同仁一线以西年均温低于4.0℃，气候寒冷，植被稀疏。永登-兰州-陇西一线以西地区以及土默特左旗-原平-五台以北年均温为4.0～7.0℃，气候也是相对寒冷，不利于植物生长。长武-志丹-阳泉一线以北的大部分地区温度在7.0～10.0℃，很多植被可以生长，农业牧业都有所发展。此线以南的陕西关中、山西中南部以及河南西北部年均温在10.0～14.0℃，大部分植被生长茂盛，农业发达[13-14]。

从年均温分布面积上看，在黄土高原，年均温小于4.0℃的寒冷干旱地区占总面积的3.20%，年均温为 4.0～7.0℃的较寒冷地区占总面积的11.47%，年均温为7.0～10.0℃的较温暖地区占总面积的54.63%，年均温10.0～14.0℃占总面积的30.71%。黄土高原7.0～14.0℃面积占整个区域面积的85%，因此，黄土高原气候适宜农牧业发展。

3 结论与讨论

黄土高原降水量和年均温空间插值表明，传统的反距离权重插值、多项式插值和径向基函数插值方法，插值误差比地统计学中的克里金方法大。对比各种插值方法，对于降水量宜采用普通克里金法进行空间插值，年均温宜采用简单协克里金法。这是因为降水量受高程影响不大，而年均温受高程影响较大，因此，将高程作为第2影响因素引入到空间插值中的协克里金方法，利用地理位置、高程和年均温的空间变量相关性，进行空间估计，大大提高了插值精度和合理性。因此，不能笼统地说哪种插值方法最好，必须在特定条件下，针对特定区域的特定项目选择最佳插值方法。

黄土高原降水量偏少，总体分布呈现西北低、东南高的态势，界限明显。降水量大于200 mm的半湿润和半干旱面积占整个区域面积的4/5以上，因此，黄土高原以半湿润-半干旱气候为主。黄土高原年均温较低，总体分布呈现西北低、东南高的态势，界限也很明显。年均温7.0～14.0℃面积占整个区域面积的85%，黄土高原气候适宜农牧业发展。

数学模型与地理信息系统的集成将是第4代地理信息系统研究中的最重要问题之一，而空间插值模型是数学模型的主要方面，空间插值方法的应用与进一步研究有着广阔的前景。目前用于插值的软件还有很多，如 ANUSPLIN、PRISM 和 GIDS等[14]。对空间插值方法而言，没有绝对最佳的方法，只有在特定的条件下，对于特定区域实际情况的最佳方法，在考虑插值误差的同时，还要顾及到实用性，即是否具有简便的插值检验方法，从而选出最优插值方法。

[1] Mohamed A S.Reliabilty estimation of rainfall-runoff models[D].New York:State University of New York，1999.

[2] Lamn.Spatial interpolation methods:a review[J].The Amercian Cartographer，1983，10(2):129-149.

[3] Dirks K N，Hayl E，Stow C D，et al.High-resolution studies of rainfall on Norfolk Island.PartⅡ:interpolation of rainfall data[J].J.Hydrol，1998，208(3/4):187-193.

[4] Borga M，Vizzaccaro A.On the interpolation of hydrologic variables:formal equivalence of multiquadratic surface fitting and Kriging[J].J.Hydrol，1997，195(1/4):160-171.

[5] Hevesi J A，Flint A L，Isto J D.Precipitation estimation in mountainous terrain using multivariate geostatistics.part I:structural analysis[J].J.Appl.Meteor，1992，31:661-676.

[6] 中国科学院水利部水土保持研究所.黄土高原水土保持数据库[EB/OL].[05-08-20]，http://www.loess.csdb.cn/.

[7] 党安荣，贾海峰，易善桢，等.ArcGIS 8 Desktop地理信息系统应用指南[M].北京:清华大学出版社，2005.

[8] 侯景儒，黄竞先.地质统计学的理论与方法[M].北京:地质出版社，1990.

[9] 朱会义，贾绍凤.降水信息空间插值的不确定性分析[J].地理科学进展，2004，23(2):34-42.

[10] 任朝霞，杨达源.近50a西北干旱区气候变化对农业的影响[J].干旱区资源与环境，2007，21(8):48-52.

[11] 石朋，芮孝芳.降水空间插值方法的比较与改进[J].河海大学学报:自然科学版，2005，33(4):361-365.

[12] 王景雷，孙景生，张寄阳，等.基于 GIS和地统计学的作物需水量等值线图[J].农业工程学报，2004，20(5):51-54.

[13] 范敏杰，袁玉江，魏文寿，等.新疆伊犁地区夏季平均最高气温的重建和分析[J].干旱区研究，2008，25(1):75-81.

[14] 阎洪.薄板光顺样条插值与中国气候空间模拟[J].地理科学，2004，24(4):163-168.