基于Matlab的模糊PID控制器设计与仿真研究
2010-05-05何鹏
何鹏
0 引言
PID控制是最早发展起来的控制策略之一。由于其算法简单,鲁棒性好和可靠性高.被广泛应用于工业过程控制。在PID控制中。一个至关重要的问题是PID参数(比例系数、积分时间、微分时间)的整定。参数整定的优劣不但会影响到控制质量,而且还会影响到控制系统的稳定性和鲁棒性。而实际工业生产过程往往具有非线性、时变等不确定性干扰。常规 PID控制器经常出现参数整定不良、控制性能欠佳,且对运行工况的适应性较差等情况。[1]
针对以上问题,长期以来,人们一直在寻求PID控制器的自动整定技术,以适应复杂的工况和高指标的控制要求。模糊控制是一类应用模糊集合理论的控制方法,不需要被控对象的精确数学模型,因而特别适用于一些大滞后、时变、非线性的复杂系统。
将模糊控制和传统PID控制相结合组成模糊PID控制器,不但具有PID控制精度高等优点,又兼有模糊控制灵活、适应性强的优点,是近年来控制领域十分活跃的一支分支。[2]
1 模糊PID控制结构
模糊PID控制器以误差e(k)和误差变化率ec(k)作为输入,可以满足不同时刻的e(k)和e c(k)对PID参数整定的要求。利用模糊控制规则对PID参数进行修改,便构成了模糊PID控制器,其结构如图1所示。

图1 模糊PID控制结构
PID参数模糊自整定是找出PID三个参数与误差e(k)和误差变化率ec(k)之间的模糊关系,在运行中通过不断检测,根据模糊控制原理来对3个参数进行在线修改,以满足不同e(k)和e c(k)对控制参数的不同要求。从而使被控对象有良好的动态、静态性能。
2 模糊控制器的实现
2.1 控制规律
通常不同的偏差|e|和偏差变化率|ec|控制器参数Kp、Ki、Kd的整定要求不同,控制规则如下:
(一)当|e|较大时,为了使系统具有较好的跟踪性能,应取较大的Kp和较小的Kd,同时为避免出现较大的超调,应对积分作用加以限制,通常取Ki=0。
(二)当|e|中等大小时,为了使系统具有较小的超调,Kp应取得小些。在这种情况下,Kd取值大小对系统影响较大,应取得小一些.Ki的取值要适当。
(三)当|e|较小时,为了使系统具有较好的稳定性能,Kp和Ki均应取得大些。同时,为了避免系统在设定值出现振荡,并考虑系统抗干扰性能,当|ec|较大时Kd可取得小些,当|ec|较小时Kd可取得大些。[3]-[4]
2.2 输入量和控制量的论域及模糊参考集
取系统误差e,系统误差的变化ec为输入量,取PID控制器参数:Ukp、Uki、Ukd为控制量。
模糊参考集取为:{NB,NM,NS,ZO,PS,PM,PB}
论域为:{-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6}若不同的话,只需改变Matlab中输出对应的隶属度函数,但模糊控制器的规则不变,结果大同小异)当实际测量值与所设[-6,+6]范围不一致,而在〔a,b〕之间范围,可以由变换式转化为[-6,+6]之间的量Y:

令误差量化因子为q=2×6/[x-(-x)]=6/x,这样对于基本论域中的精确值X∈[-x,x],可以用如下公式求出论域[-6,6]中的元素b

采用三角形隶属度函,隶属度函数数曲线为:
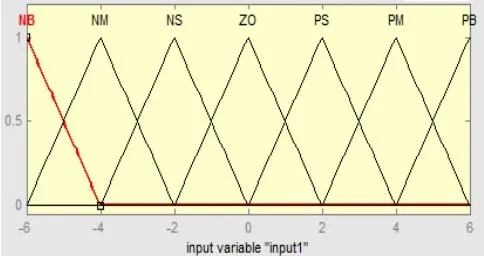
图2 三角函数隶属度曲线图

表1 输入量与控制量的隶属度函数赋值表
2.3 模糊关系矩阵
由控制经验可得模糊控制规则见表2
2.4 模糊判决
模糊判决即解模糊过程是把语言表达的模糊量映射到精确的调整量,也就是根据输出模糊子集的隶属度计算输出的确定值,控制量的反模糊化采用加权平均法,计算公式如下:


表2 Kp、Ki、Kd模糊控制规律
2.5 仿真研究
利用Matlab中的SIMULINK和FUZZY工具箱建立仿真系统如图,设被控对象系统传递函数为:

图中的模糊逻辑控制器中隐含了输入输出关系的FIS需要利用行命令或者GUI编辑函数事先建立。
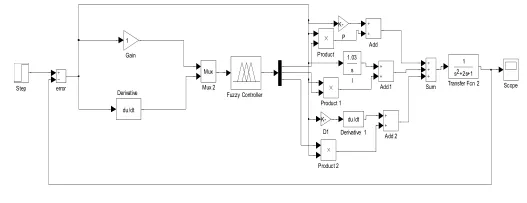
图3 模糊自整定PID仿真系统图
常规PID控制阶跃响应如图4(a)所示,模糊自整定PID阶跃响应如图(b)所示,通过对比可见,由系统仿真阶跃响应对比可以看出,与常规PID控制相比,采用模糊自整定PID控制,系统超调量为明显减少,调节时间为与上升时间也明显缩短。--见图4

图4 系统阶跃响应曲线
3 结论
本文将模糊控制理论和MATLAB有机结合通过对PID参数自整定模糊控制器的设计与仿真研究,介绍了系统实现模糊控制的一般方案,具有易于熟悉,输出量连续,超调量小等特点,能够达到较好的动态特性和静态特性。
[1]刘曙光,魏俊民,竺志超.模糊控制技术.北京:中国纺织出版社,2001.
[2]爱民编著.模糊控制技术.西安:西安电子科技大学出版社,2008.
[3]夏红,赏星耀,宋建成.PID 参数自整定方法综述.浙江科技学院学报,2007,15(4):236-240.
[4]韩力群主编,智能控制理论及应用.北京:机械工业出版社,2008.
[5]黄忠霖,黄京编著,控制系统MATLAB计算及仿真.北京:国防工业出版社,2009.
