基于遗传算法支持向量机的虚拟仪器动态补偿

马 超，李世平，张 进

（第二炮兵工程学院，陕西 西安 710025）

1 引 言

现在常用的动态测试误差补偿方法是对其输出信号进行后处理，增加动态补偿环节。近几年，有不少学者利用神经网络的方法对系统进行动态误差补偿，但是神经网络的不足之处在于：（1）存在过学习问题，影响其整体的泛化能力；（2）由于训练结构的关系会使补偿环节参数的确定存在一定的随机性；（3）当样本数据有限时，结果偏差较大。鉴于以上原因，运用神经网络的方法提高测量精度所付出的代价是运算量很大。为此，该文利用支持向量机（Support Vector Machines，SVM）对虚拟仪器进行动态补偿，能够在一定程度上解决上述问题。

支持向量机由美国N·Vapnik教授提出，是在小样本情况下发展起来的统计机器学习理论，能有效地解决“维数灾难”和“过学习”等问题。

该文提出了利用遗传算法对支持向量机进行优化且自动选择最优参数。仿真结果表明，利用该方法可以解决传统参数选择方法的缺点，并且动态误差补偿的效果非常明显。

2 动态补偿原理

由于测试系统存在一定的响应滞后，因此输出信号y（t）与被测信号x（t）之间存在较大的动态测试误差。为提高测试精度可使测试系统输出通过一个补偿器，用补偿器的输出y^（t）替代 y（t）从而达到修正动态误差的目的，其原理如图1所示。

图1 动态补偿原理示意图

实际应用中的动态补偿环节可用单变量差分方程予以描述：

式中：z-1——延迟算子；

n，m——阶次；

e（t）——输出噪声。

式（1）的向量形式为：

式中：b——常数，ω=（-a1，…，-an，b0，b1，…，bm）T，Xt=（z-1y^（t），…，z-ny^（t），y（t），z-1y（t），…，z-my（t））T。

从式（2）来看，动态补偿器的构造过程其实就是对补偿模型进行辨识，求取参数ω和b的过程。动态补偿器原理如图2。

3 标准SVM建模方法

SVM的基本思想是通过非线性变换将n维样本从原空间映射到高维特征空间中，并从中构造最优线性回归函数，设给定的训练样本为：

首先用一个非线性映射φ把数据映射到一个高维数特征空间，然后在高维特征空间中进行线性回归，设回归函数为：

优化问题是最小化：

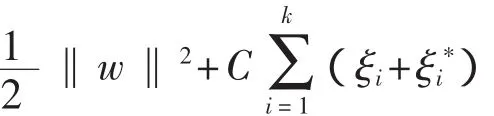
约束为：

这是一个二次优化问题，其对偶问题为：

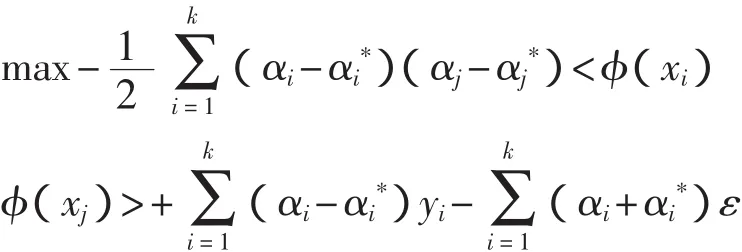
约束为：

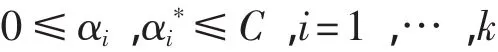
解这个二次优化，可以得到α的值，w的表达式为：

于是回归函数的表达式为：

可以证明，只要满足Mercer条件核函数K（x，y），可以代替高维空间中的内积运算，从而避免了复杂的高维计算问题。按照KKT定理，可以得到b的计算式如下：

4 遗传算法优化步骤

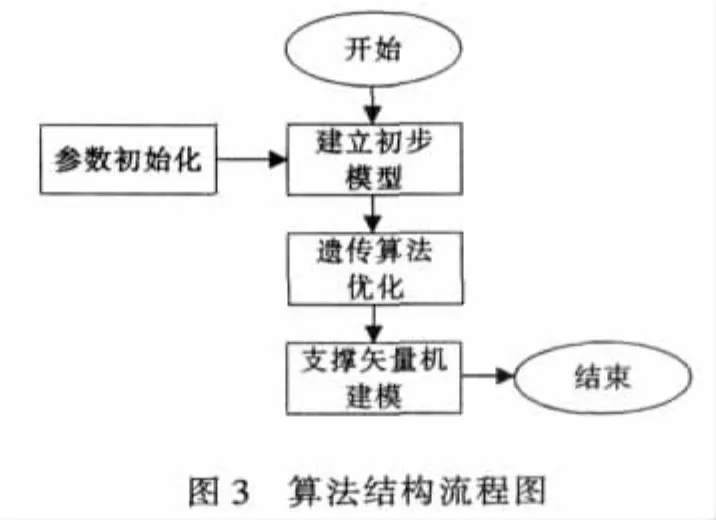
由支持向量机回归方法可以看出，在支持向量机优化过程中，不敏感系数ε、惩罚系数C以及核函数中的结构参数无法在优化过程中自动选择，只能凭经验或是交叉验证的方法确定。这样，一方面缺乏理论基础，另一方面也无法保证所选择的参数是最优的。而遗传算法作为一种新的全局优化搜索算法，正好可以对支持向量机中的这些参数进行优化选择，从而不仅使支持向量机模型中的这些参数的选择更具理论性，而且可以保证模型的最优。基于遗传算法的支持向量机的算法结构流程图如图3。

遗传算法具体实施过程：

（1）适应度函数fit（C，σ，ε）。对于给定染色体ri，其适应度函数按下式计算：

式中：yi——数据实际值；

Ymax——ri所在世代中Yi的最大值。

（2）对变量 C，σ，ε赋初值。

（3）染色体编码。染色体r采用二进制编码，每个算子由三段编码组成，即：

r=A1，A2，A3

其中 A1，A2，A3分别为 C，σ，ε 的代码表示段。

（4）种群初始化。令gen=0，在各变量取值范围之内，随机生成规模为N的初始种群R。

（6）染色体变异。采用pm的概率进行染色体变异。随机选取染色体上一位，将其按照0→1，1→0的规则进行变异。然后检验变异后染色体是否在变量取值范围内，如不满足则重新进行变异。

（7）计算连续五代染色体平均适应度差值，记其最大差值为ζ，如果ζ≤μ（μ为给定差值下限）或者gen≥Niter（Niter为给定最大进化代数），则停止进化，输出该种群中的最优结果。否则gen=gen+1，转步骤（5）。

5 实际虚拟仪器动态补偿

实验中，构建一个虚拟仪器数据采集系统，将FLUKE5700作为标准信号源输入，通过PCLD-8115传输，利用PCL-818HD数据采集卡进行采集，然后在虚拟仪器程序软件LabVIEW中显示（激励信号采用单位阶跃信号）。所采集动态信号如表1。

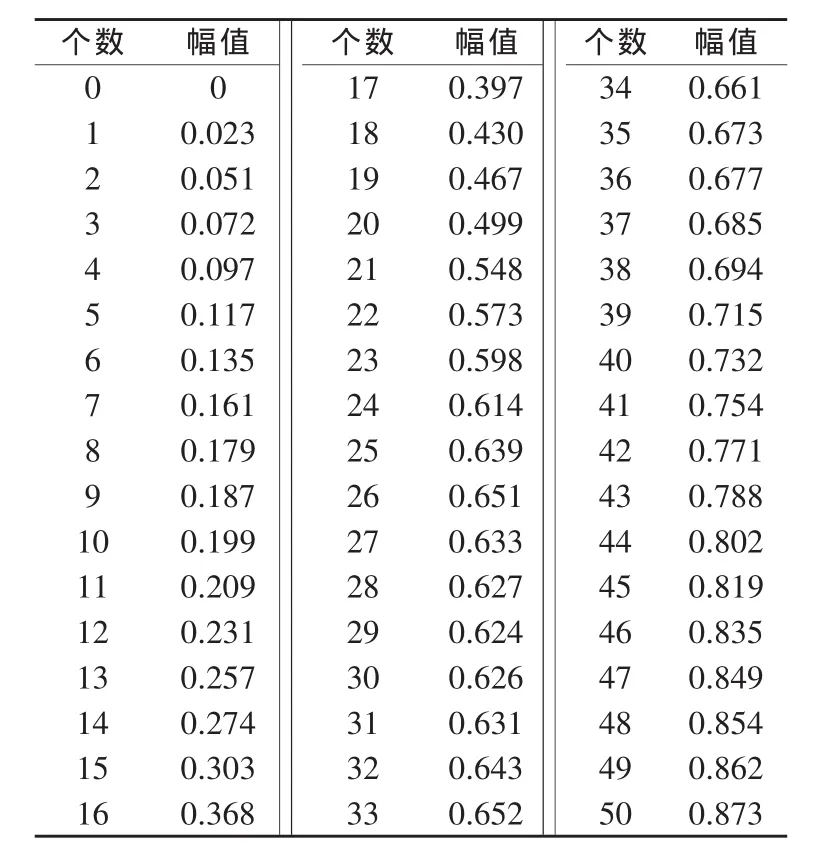
表1 采集到的数据1）

补偿模型中遗传算法参数NIND（个体数目）=60，Pm（变异概率）=0.75，Pc（交叉概率）=0.01，由遗传算法得出的标准支持向量机参数gam（规则化参数）=1.60237e+003；sig2（核函数参数）=1.602 21e-003；补偿结果如图4。

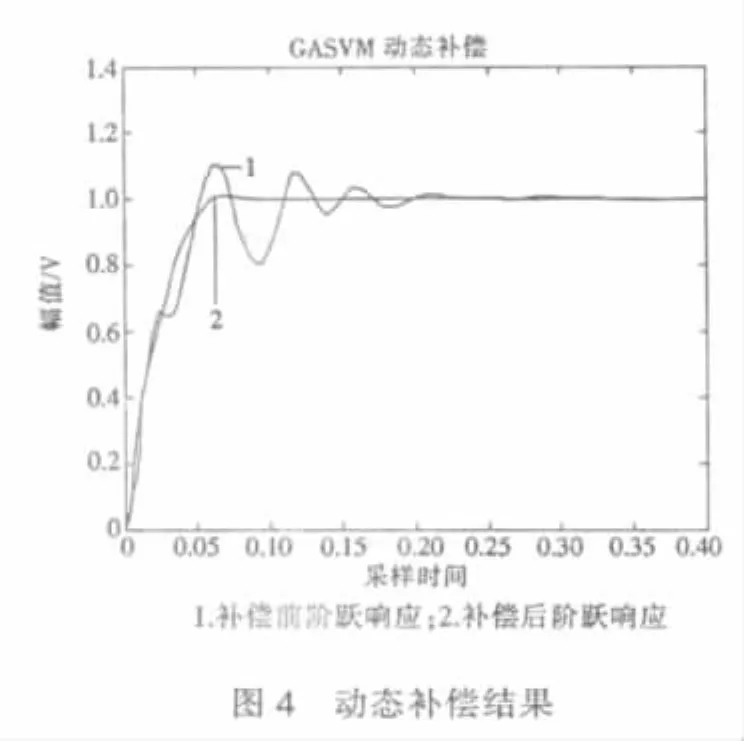
如图4所示，经补偿后的测试系统其相应的动态性能指标得到了较大提高，y（t）的振荡得到了有效抑制，超调量明显减小，同时达到稳态的时间约缩短为补偿前的1/5，动态误差也得到了较好的补偿。

6 结束语

该文详细论述了标准SVM的基本原理与辨识方法，并讨论了SVM在进行动态补偿器构造中的实际运用。通过以上仿真和实验可以看出，利用遗传算法对标准SVM进行优化后，其动态补偿效果非常明显。因此，遗传算法支持向量机（GASVM）为虚拟仪器动态补偿提供了一种可靠的方法，理论和实验均证明该方法可行。

[1]张国云.支持向量机算法及其应用研究[D].长沙：湖南大学，2006.

[2]李亚楠，耿伯英.基于支持向量机的传感器非线性动态补偿[J].传感器技术，2005，24（12）：19-21.

[3]雷 剑.基于SVM和遗传算法的建模与全局寻优方法[J].科技广场，2008（5）：120-122.

[4]喻俊馨，王计生，黄惟公.基于神经网络和支持向量机的故障诊断[J].西华大学学报：自然科学版，2008，27（3）：24-27.

[5]王 凌.智能优化算法及其应用[M].北京：清华大学出版社，2004.

[6]杨乐平，李海涛.LabVIEW程序设计与应用[M].2版.北京：电子工业出版社，2005.

[7]费业泰.误差理论与数据处理[M].北京：机械工业出版社，2003.

[8]赵洪波.基于遗传算法的进化支持向量机研究 [J].绍兴文理学院学报，2004，24（9）：25-28.