多目标水库群调度的性能评价模型

[印度 ]G.S.乔希 K.古普塔

王艳菊 王 珏 译自荷刊《水资源管理》2010年第1期

大多数的水资源工程可直接或间接地造福于人类。为了确保水资源工程的可行性、合理性和社会可接受性,有必要在工程规划、设计和运行阶段适当考虑其供水可靠性、发电量、收益及防弃水能力。为了对一个水资源工程进行性能评价以及方案设计和调度策略的选择,提出了采用可靠性、回弹性和脆弱性 3个标准作为一种概率度量,并根据具有众多调度策略的一座供水水库的性能说明这 3个标准的用途。另一项研究建立了一个简单的交互式综合水资源配置模型(IWAM),用于辅助设计和决策人员在考虑社会经济、环境和技术等各个方面的情况下,对一座蓄水水库中的有限水资源进行优化配置,以供给各个不同的用水部门。在印度的高韦里(Cauvery)河上游流域,对两个不可同单位度量的目标,即农作物面积的最大化和净经济效益的最大化以及对查利雅(Chaliyar)河流域的灌溉泄水量和发电量最大化进行了研究;在克里希纳(Krishna)河上游流域,则通过水库调度准则实现灌溉泄流量和发电泄流量最大化。然而,在印度还没有任何使综合系统的性能指标最大的研究(包含工业、生活和灌溉供水水量和时间可靠性、水力发电目标、涵盖运行维护费用和防弃水的净经济效益等调度目标)。

本文建立了多目标水库群调度的性能评价模型及流域多目标水库群调度中与每个性能度量标准相应的性能指标,并将系统性能指标(SYSPI)作为系统整体性能的度量指标,它是以上5个性能指标的函数。已研究出一种方法来计算每座水库为满足不同目标所分配的泄水量,制定河流强制泄流量的合理分配方案,并进行多目标调度系统性能评价。将所提出的方法应用于印度讷尔默达河流域的 9个水库群。该方法的整体框架见图1。

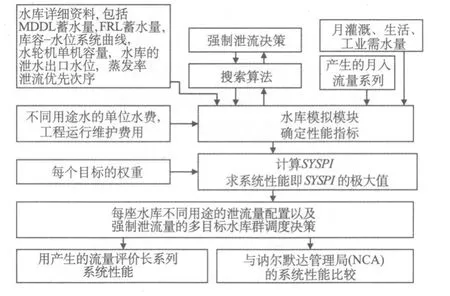
图1 多目标水库群调度的性能评价模型示意

1 问题的表达

在这项研究中,建立了多目标水库群调度的性能评价模型,包含以下5个目标:

(1)满足工业、生活和灌溉用水需求的水量可靠性;

(2)满足工业、生活和灌溉用水需求的时间可靠性;

(3)满足系统发电量;

(4)所获收益满足工程运行维护费用;

(5)通过防止弃水事件减少因系统弃水而产生的水量和能量损失。

针对以上每个目标,提出以下性能指标:

(1)水量可靠性指标 (VRI)(水的可用性指标);

(2)时间可靠性指标 (TRI)(水的可靠性指标);

(3)水力发电量指标(HPI)(水电潜力指标);

(4)经济效益指标(ECBI)(经济效益指标);

(5)防弃水指标(SPPI)(弃水事件指标)。

VRI和 TRI用来衡量供水水量和时间可靠性,HPI用来衡量水电能。由于任一工程必须通过获得收益补偿其运行维护费用,因此可引入经济效益指标 ECBI对工业、生活和灌溉用水费进行独立核算。

任何弃水事件都表示系统有水量和能量损失。因此应尽量减少弃水事件的发生以保护下游免受水库溢流引起的洪灾。SPPI作为弃水事件及其预防的指标,还必须协调好强制泄流和弃水事件。对于系统中的每座水库来说,最小化弃水事件指标并不总能使发电量最大,因为发电量还受制于电站压力输水管的容量。而且,库群中的某些水库在设计中可能本来就没有考虑其发电目的。对于这样的水库,弃水最小化目标仅是使损失量最小,进而防止能量损失并防止下游遭受洪水。

以上的调度准则对于水库群性能评价非常必要,其中水库群将以综合方式进行调度,并且水库管理局必须确定每座水库泄入河道的月强制泄流量。

1.1 目标函数

系统性能最大化目标函数采用多目标分析中的权重法来表示,它是每个性能指标乘以反映其相对重要性的权重因子之和,用公式表示为:

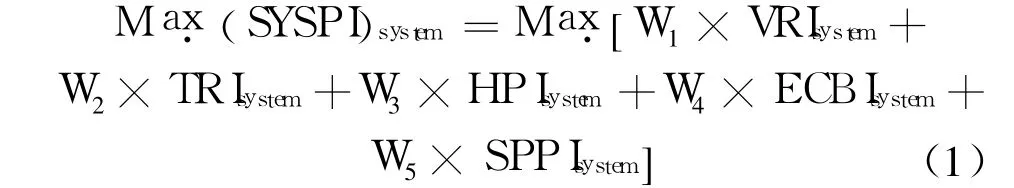
式中 W1、W2、W3、W4和 W5分别为分配给 VRIsystem、TRIsystem、HPIsystem、ECBIsystem和 SPPIsystem的 权重;VRIsystem为水库群的水量可靠性指标;TRIsystem为水库群的时间可靠性指标;HPIsystem为水库群的水力发电量指标;ECBIsystem为水库群的经济效益指标;SPPIsystem为水库群的防弃水指标。

权重隐含着价值判断。确定目标函数的这组权重必须考虑发展的和社会的优先权。

依据水库的月强制泄流量决策变量并不能直接确定公式(1)中的系统性能指标,因此,这里所采用的方法是将搜索算法与模拟模块结合来解决优化问题。

1.2 搜索算法

通过对水库群中从上游至下游的每座水库实施顺序搜索算法来求得目标函数(公式(1))的极大值。通过反复的迭代计算最终得到决策变量即强制泄流量决策的最优值。模型优化步骤如下:

(1)从强制泄流量决策变量的初始估计值开始进行搜索;

(2)采用牛顿 -拉弗森(Newton-Raphson)迭代公式;

(3)检验是否满足迭代终止准则,若不满足则重复步骤2。

迭代终止准则的确定以强制泄流量决策变量没有进一步的变化以及在最新的迭代阶段系统性能指标的极大值没有更多的改善为准。

搜索迭代的牛顿 -拉弗森公式如下:

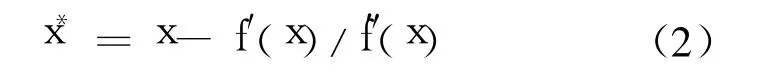
式中 x*为决策变量即强制泄流量的改进值;x为决策变量即强制泄流量的当前值;f′(x)为目标函数的一阶导数;f″(x)为目标函数的二阶导数。

给定决策变量 x(月强制泄流量)的当前值和目标函数的一阶以及二阶导数的值,采用以上公式即可确定一个改进值 x*。

1.2.1 与模拟模块相关联的搜索算法

由于公式(2)中采用的一阶导数和二阶导数 f′(x)与 f″(x)不能够通过解析方法得到其解,因此必须采用如下有限差分数值计算公式得到:

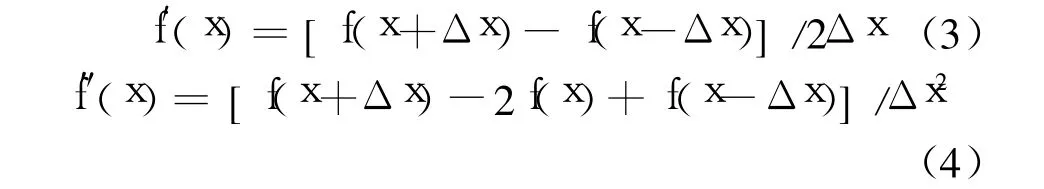
式中 f(x+Δx)为强制泄流量决策变量(x+Δx)的目标函数值;f(x-Δx)为强制泄流量决策变量(x-Δx)的目标函数值;x为强制泄流量决策变量;Δx为决策变量,即强制泄流量 x值域内的任意值。

要得到二阶导数的有限差分近似值,至少需要3个目标函数值。搜索算法必须与模拟模块相结合来确定目标函数的5个性能评价指标,在搜索循环中每应用一次公式(2)则模拟模块被执行 3次。搜索算法用强制泄流量决策变量的改进值重复执行模拟模块,并采用公式(3)和(4)来寻求强制泄流量决策的最优值。直到强制泄流量决策变量的值没有进一步的变化则循环算法停止。

1.2.2 模拟模块

模拟模块采用 LAST模型生成的入流量数据模拟100a的强制泄流量以得到目标函数值。每座水库的月强制泄流量规定在其上下限范围之间。每座水库月强制泄流量的上限和下限采用乔希(Joshi)和古普塔(Gupta)2009年提出的方法进行计算,即自下游水库向上游水库逐一计算,以满足水库群中终端水库所需要的月流量。终端水库所需要的月流量通过分解已知的年需求流量得到。

性能指标公式如下:

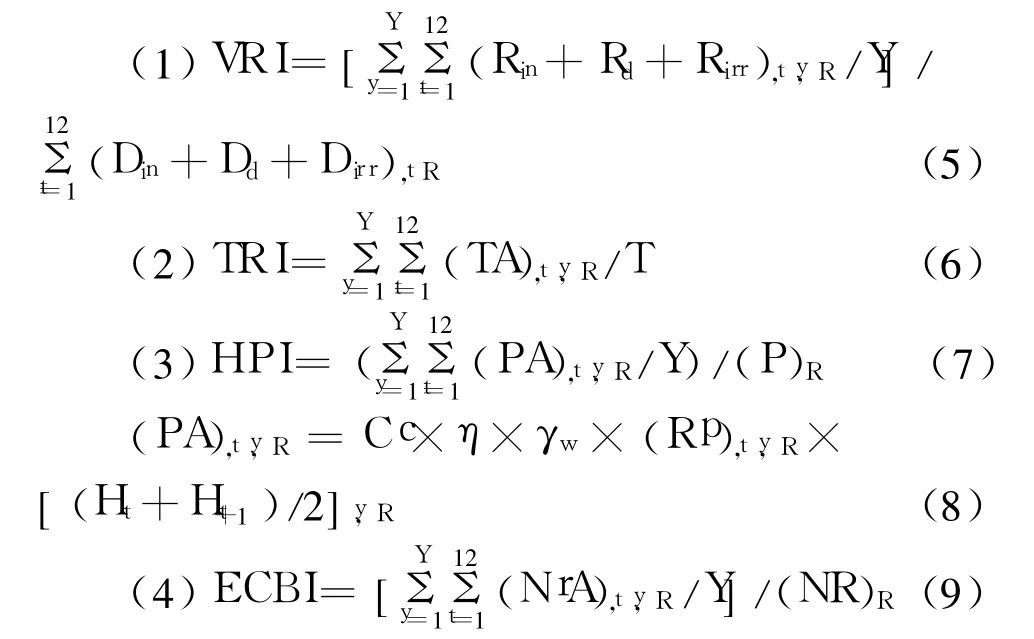
水库 R第 y年特定月份 t的货币净收益(NR)t,y,R以及水库 R计划的供水年货币收益(NR)R如下:

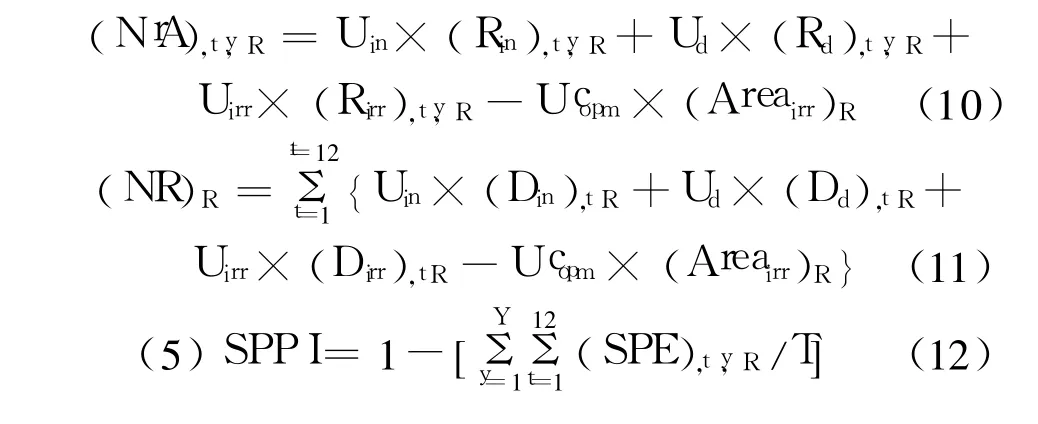
2 讷尔默达河流域概况

讷尔默达河流域位于印度中部,地理坐标为东经72°32′～81°45′,北纬21°20′～23°45′,控制流域面积为 98796 km2,平均海拔高为760m。讷尔默达河发源于印度中央邦(Madhya Pradesh State)阿玛勘塔(Amarkantak)的迈克尔(Maikal)山脉,向西流1312 km后汇入位于印度古吉拉特邦(Gujarat State)巴鲁奇县(Bharuch district)西部的坎贝(Cambay)海湾。流域中现有工程主要有巴尔纳(Barna)、塔瓦(Tawa)、戈拉尔(Kolar)、苏克塔(Sukta)和巴尔吉(Bargi)工程。另外还有如英迪拉萨格尔(Indirasagar)坝 、翁卡列什瓦 (Omkareshwar)坝 、玛呵什瓦(Maheshwar)坝和萨达尔萨罗瓦尔(Sardar Sarovar)坝正在建设中。已建成的巴尔纳 (BA1)、塔瓦(TA2)、戈拉尔(KO3)、苏克塔(SU4)和巴尔吉(BG5)水库均各自独立运行,对于系统以综合方式运行调度所需要的强制泄流量并未明确规定。目前仅规定了现有水库季风季节(6月15日 ～10月15日)的调度策略。而且现有水库的现行调度策略只考虑了保持某个月份水库水位与月平均流量相一致,并未考虑水库的入流量和有效库容。本文的研究旨在减少现行调度策略的缺陷。

将所提出的多目标水库群调度的性能评价模型应用于印度讷尔默达河流域水系,以验证其应用情况。系统约束为从上游水库下泄到下游水库的流量应满足在终端水库即萨达尔萨罗瓦尔(SS9)处的年入流量要求,即120.24亿 m3。

农作物的月需水量根据讷尔默达管理局(NCA)推荐的作物栽培模式进行计算。公式(1)中的每个目标函数的权重均取为0.2,即设定每个目标的重要程度相同。不同用途泄水水量分配和未来实施水库群综合调度的规划指导原则如下。

(1)供水的优先顺序为工业和生活需水量、灌溉需水量和发电需水量。模拟模块依据这种优先顺序运行。

(2)水库群放空水库的顺序为自下游水库向上游水库,以满足下游需水量;水库群蓄水顺序为自上游水库向下游水库。

基于这些指导原则,对强制泄流量的值域(即上下限)自下游水库向上游水库逐一进行了计算,同时通过搜索算法在以上的强制泄流量值域范围内自上游向下游水库寻求其最优值,以求得系统性能的极大值。

3 与模拟模块相关的搜索算法结果

系统性能指标取得极大值时的各个性能指标VRI、TRI、HPI、ECBI和 SPPI的值见表1。从表1可以看出,供水水库用于工业、生活和灌溉供水的VRI大于 80%,而用于供水和水力发电的水库其值则大于 90%。

NCA计算得出英迪拉萨格尔水库(IN6)的年强制泄流量为100亿 m3,但是并没有用公式表达月强制泄流量策略。本文成功地应用性能评价模型计算了月强制泄流量,根据计算,英迪拉萨格尔水库(IN6)6～12月份以及1～5月份的强制泄流量(亿m3)分别为1.94、27.37、30.34、29.40、7.42、2.05、1.25,以及1.03、2.40、1.24、0.42、0.55,年强制泄流量为105.41亿 m3。该方法所得到的年强制泄流量为105.41亿 m3,与 NCA计算的结果(100亿 m3)相比较,其优点是能表示每月的强制流量值。

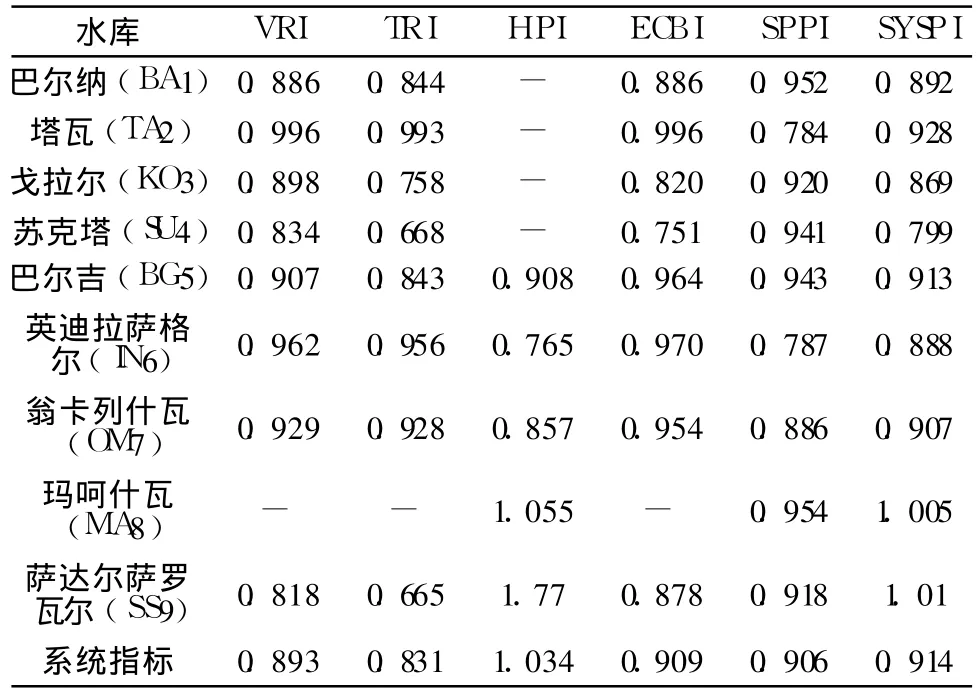
表1 多目标水库群调度的性能评价模型计算的性能指标值

4 系统性能评价

由性能评价模型计算得到 HPI,然后将其用来评价水库群发电的系统性能。经分析得出,整个开发期内系统的潜在发电量(4678.79 GW◦h)比NCA规划的系统潜在发电量(4521.4 GW◦h)高出157.39 GW◦h。结果表明,该方法能使系统发电量增加 3%。

由性能评价模型计算得到的 ECBI结果表明,除了戈拉尔电站和苏克塔电站之外的所有工程运行和维护费用均能够从用水收费中得到补偿。经济效益分析的应用有助于决策者分析水库群不同规划策略获得的净经济效益,以及改变各种用途的用水水费所获得的净经济效益。

5 性能指标重要性评价

为了通过赋予不同权重改善系统供水和发电设施,对每个性能指标的重要性进行了评价。在对每个指标赋予权重的基础上考虑了如下7套备选方案。

(1)方案1～5。对于改善系统供水和发电设施的每个性能指标的重要性进行评价时,设其中一个性能指标权重为1而其余性能指标权重均为 0。

(2)方案 6。对于改善系统供水和发电设施的每个性能指标的重要性进行评价时,设 VRIsystem和HPIsystem的权重均为0.5,其余性能指标权重均为 0。

(3)方案7。对于改善系统供水和发电设施的每个性能指标重要性进行评价时,设5个性能指标的权重均为0.2。

各套备选方案系统性能取得极大值情况下的VRIsystem和 HPIsystem的结果见表2。由表2可以看出,目标函数包含5个性能指标的方案7得到的VRIsystem和 HPIsystem的值最大。从而得出,在系统性能取得极大值情况下,考虑所有5个性能指标VRIsystem、TRIsystem、HPIsystem、ECBIsystem和 SPPIsystem与仅考虑其中一个性能指标或者仅考虑 VRIsystem和HPIsystem情况相比,前者得到的发电和供水目标要优于后者。

6 结 语

提出了印度讷尔默达河流域多目标水库群的规划月综合调度模式的性能评价模型及其计算公式。共考虑了5个调度目标,即实现需水的水量可靠性、需水的时间可靠性、发电量目标、工程收益以及减少系统弃水事件。

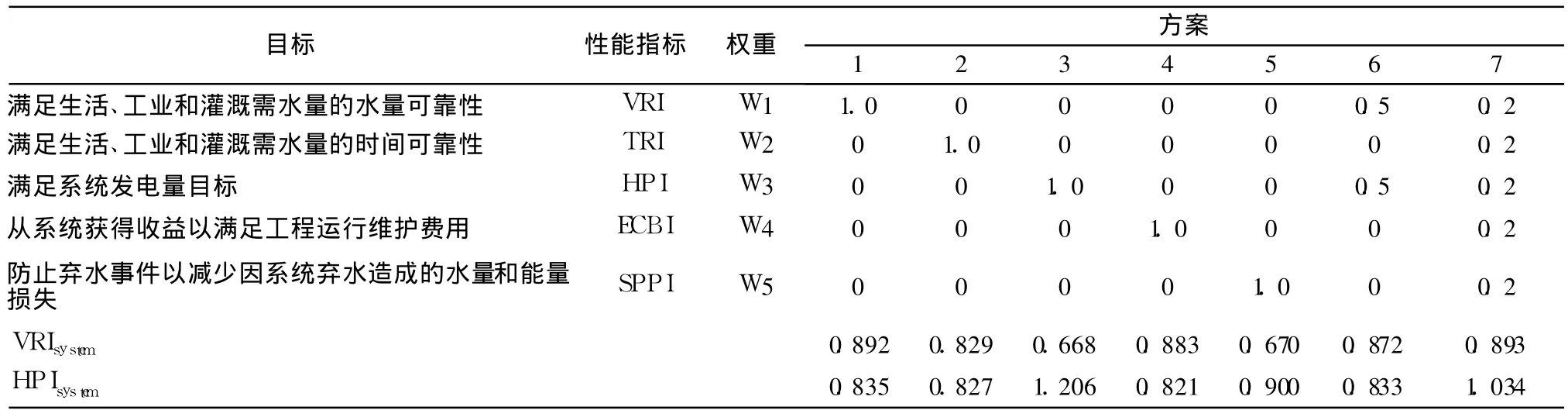
表2 各备选方案每个性能指标的指定权重

采用一种搜索算法在系统性能指标最大情况下求得水库群每座水库的月强制泄流量以及与月入流量和水库蓄水量有关的用于不同目的的泄流量。采用多目标水库群调度的性能评价模型对系统性能进行评价。结果与 NCA规划值相比较表明,对供水和发电可靠性,本文所提出的方法能够提供出一个可接受的水平。文中所提出的多目标水库群调度的性能评价模型,若设置任一目标权重为1而同时其余目标权重为 0,则也可用于单目标模型。同理,设定任意两个目标权重各为0.5,其余目标权重为 0,则可用于双目标模型。