在有限元软件中开发实现Duncan-Chang本构模型的方法研究

2010-04-28吴桂兰迟守旭李永华

水利水电工程设计 2010年4期

吴桂兰迟守旭李永华

随着水利事业的发展,对于一些大型重要结构,除利用规范进行常规计算外,都要求进行三维有限元计算,以保证结构的设计合理性。水利工程中,一个比较棘手的问题就是土力学问题,但是,目前国内流行的大型有限元通用计算软件,大多没有考虑到此方面的要求。

本文根据此类现象,提出了一种解决方法:利用现有的大型有限元通用软件(例如ANSYS,ABAQUS等)丰富的前后处理功能,在计算模式中嵌入Duncan-ChangE-B模型本构关系,扩大此类软件的应用范围,使其能够利用此本构关系进行土体有限元计算。

1 岩土本构模型的比较与选择

严格说来,像土、砂砾石、块石等材料,具有较强的非线性和非弹性特性,有些弹塑性模型虽能在一定程度上模拟土石体的变形和应力特性,但是,总起来说不够理想,并且,数学模型中所需数据是与实验水平紧密联系的,因此,试验水平的高低也在一定程度上决定了土石体数学模型的发展。目前广泛应用于岩土工程的计算数学模型主要有:Duncan-ChangE-v模型、Duncan-ChangE-B模型、耐勒K-G模型、清华非线性解耦K-G模型、双屈服面弹塑性模型(或南水模型)等。对于土石体的计算,在各种因素综合作用下,用哪种方法计算才是最合理的,目前还没有定论,本文采用应用时间较长、工程经验较多、试验数据较容易收集的Duncan-ChangE-B模型。由于其发展较早,应用工程经验成熟,并且各个参数有成熟的试验方法和丰富的经验数值,因此,以Duncan-Chang模型为典型的非线性弹性模型在实际岩土工程计算中一直占有非常重要的地位,是分析岩土工程的重要数学模型之一。

2 Duncan-Chang本构模型数学表达式

Duncan-ChangE-B模型应力应变关系用矩阵形式可以写为[1]:

根据广义虎克定律,上式中的模量系数为:

且d22=d33=d11,d55=d66=d44,d13=d31=d23=d32=d21=d12,其他均为零。

从式(1)和式(2)可以看出,Duncan-Chang模型本构关系只与2个独立参数有关,他们是体积模量和弹性模量,可以采用下式表示:

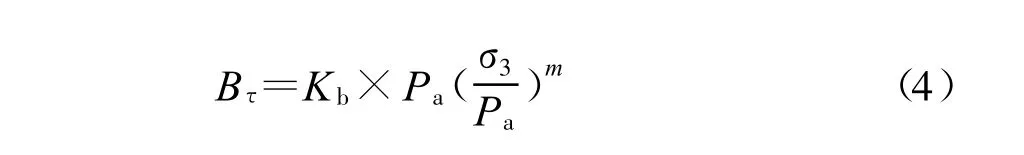
式中,c、φ分别为土体凝聚力和内摩擦角,而 φ用下式表示:

卸荷时,弹性模量采用回弹模量Eur,即:

式中,φ内摩擦角;Rf为破坏比;K为弹性模数;n为弹性模量指数;Kb为体积模量数;m为体积模量指数;Kur为卸荷弹性模量数,以上数据由实验得到。

为了准确描述土工的加卸荷过程,前面已经定义了加荷模量和卸荷模量,这需要一个判断标准,以确定两个模量的使用范围,因此,Duncan-Chang提出了加卸荷函数:

其中:

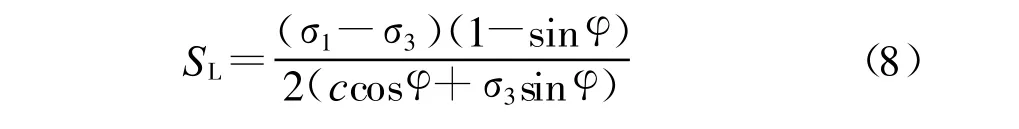
若FL＞(FL)max时,判定为加荷;FL＜0.75(FL)max时,判定为完全卸荷;若 FL介于(0.75～1)(FL)max时,弹性模量采用加荷切线模量和卸荷模量的线性插值。

3 Duncan-Chang本构模型的实现概要

根据有限元计算原理,任何有限元计算软件的计算过程都是通过刚度矩阵和边界条件(包括荷载)来实现,因此,在外部荷载一定的情况下,如果能够详细追踪单元刚度矩阵的变化过程,那么,就能够实现Duncan-Chang模型的模拟。为达此目的,可按照下述基本思路进行二次开发在现有有限元软件中实现Duncan-Chang模型。

(1)根据加荷级数分层建模。这样每施加一级荷载,就划分一层网格,然后进行求解,模拟逐级加荷过程,根据划分的网格,将不同的单元定义为不同的材料。

(2)编写程序自动提取计算结果,得到每次计算的位移和应力数值,保存输出到文本文件。根据Duncan-Chang模型,编写程序计算每一单元材料常数,并动态修改单元的弹性常数,进而对单元的刚度矩阵进行适合模型变化的修改。

(3)编写程序判断单元破坏与否,以采用相应公式修正计算过程。按照一种非线性计算方法(本文采用中点增量法)编写非线性分析命令。

(4)利用原软件后处理平台输出应力等值线;利用FORTRAN语言编写位移后处理程序,绘制模拟施工进度的位移等值线。

当然,在每个特定软件的开发过程中,其采用的工具是不一致的,但是,其实现思路都殊途同归。

4 算例测试及工程实例计算

基于以上计算思路,本文作者利用APDL在ANSYS中开发实现了Duncan-Chang模型的模拟,经编译调试后,计算了若干模型实例和工程实例,以测试计算方法的计算能力和精度。

4.1 算例测试

本次典型算例参数取自文献 [2],见表1。有限元计算时模拟常规三轴试验中的加载过程,模型尺寸为高20cm、直径8cm的圆柱试样,计算模型共剖分为3774个六面体8结点单元,结点数为4410,求解自由度为13230个,具体模型见图1。

表1 细砂土材料参数列表

根据不同围压,可以分别计算出此种材料的相应参数,列于表2。由表中数据,根据下列公式,可以得到在 σ3=0.2MPa时的(σ1-σ3)-εa曲线函数:

而由于应力水平S和(σ1-σ3)之间存在以下关系:

并且由式(9)也已知(σ1-σ3)和 εa之间得关系,另外由表2中数据可知,(σ1-σ3)f为已知,所以在在 σ3=0.2MPa时 S-εa曲线函数为:

表2 细砂土试验特征值

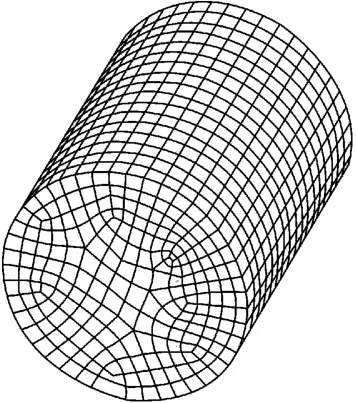
图1 模型示意图

由式(9)和式(11),在同一幅图中绘出(σ1-σ3)-εa和曲线 S-εa,如图2所示。由图2,从轴向应变与主应力差、轴向应变与应力水平比较来看,计算结果与试验结果有很好的一致性。

图2 围压为0.2mPa时采用不同方法

另外也针对不同围压的情况下,试验数据和基于ANSYS二次开发的Duncan-ChangE-B程序的计算结果对比,每一个围压下的轴向应变与主应力差与围压为0.2MPa情况下趋势一致,可以看出本文程序对模型的模拟能力令人满意。

4.2 工程实例计算

本算例对某心墙堆石坝进行了施工、蓄水等实际加载路径的数值仿真模拟。有限元计算中单元为3798个,结点2796个。静力计算时,坝体分9级填筑。堆石坝填筑过程及蓄水过程见图3。计算中采用的堆石坝的Duncan-Chang材料参数及容重列于表 3。计算中堆石坝采用新开发的 Duncan-Chang模型;基础采用D-P模型。如此定义,可以在ANSYS中实现坝体模型和地基基础的整体三维有限元计算。

图3 堆石坝坝体材料分区及荷载步示意图

计算过程中,考虑坝体材料的特性,认为堆石体和反滤料为透水材料,因此,通过渗流计算,浸润线以下的材料采用浮容重,心墙部分浸润线以下采用饱和容重。心墙认为是隔水层,水压力不作用在坝坡上,而是直接作用在心墙的上游表面。

表3 心墙堆石坝材料力学参数指标

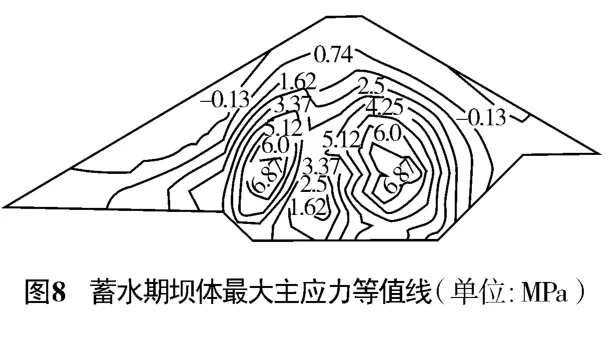
经计算,图4～6为最大剖面竣工期位移、应力图,图7～9为最大剖面正常运行期的位移、应力图(图中竖向位移以向上为“+”,向下为“-”;水平位移以指向下游为“+”,指向上游为“-”;应力以压应力为“+”,拉应力为“-”)。

从坝体位移等值线图可以看出,坝体的变形符合一般规律。由于心墙材料较软,竖直沉降最大值发生在心墙内,大约在心墙中部。竣工期上、下游变位基本对称,运行期由于水压力的作用,坝体水平位移都是向下游的,其最大值发生在心墙或心墙上游侧坝壳上部,这是由于心墙材料软,心墙对上游坝壳的约束小所致的。无论是蓄水期还是竣工期,坝体垂直向位移明显大于顺河向水平位移。因此对于以控制变位为主的堆石坝,应加强运行期垂直变形的监测。

由图5和图8可以看出,堆石坝在自重荷载的作用下,主应力大致是关于坝轴对称分布的,在接近上下游坝坡的区域等值线大致与坝坡面平行,由坡面向内、由坝顶向坝底主应力逐渐增大。

由于心墙料比坝壳料软,心墙的变形大,堆石料的变形相对小,变形不协调,于是引起应力的重新分配,心墙部分的应力会转移一部分到反滤层,致使心墙的应力低于自重应力,心墙两侧反滤层的应力高于自重应力。同时由于设置了反滤层,它会同时起到过渡层的作用,使得心墙和堆石体之间有一个过渡层,能够起到保护心墙的作用。