基于多元线性回归分析的蝶阀关闭规律函数关系研究
2010-04-23程洪霞吴建华
程洪霞 吴建华
(太原理工大学水利科学与工程学院,太原 030024)
1 蝶阀关闭角间隔点的计算机存储及直线插入法
在国内外大量的供水系统水锤分析文献中,给出了蝶阀关闭角每隔5°时,相对应的阻力系数和过流面积与阀门面积比值的离散值,见表1。
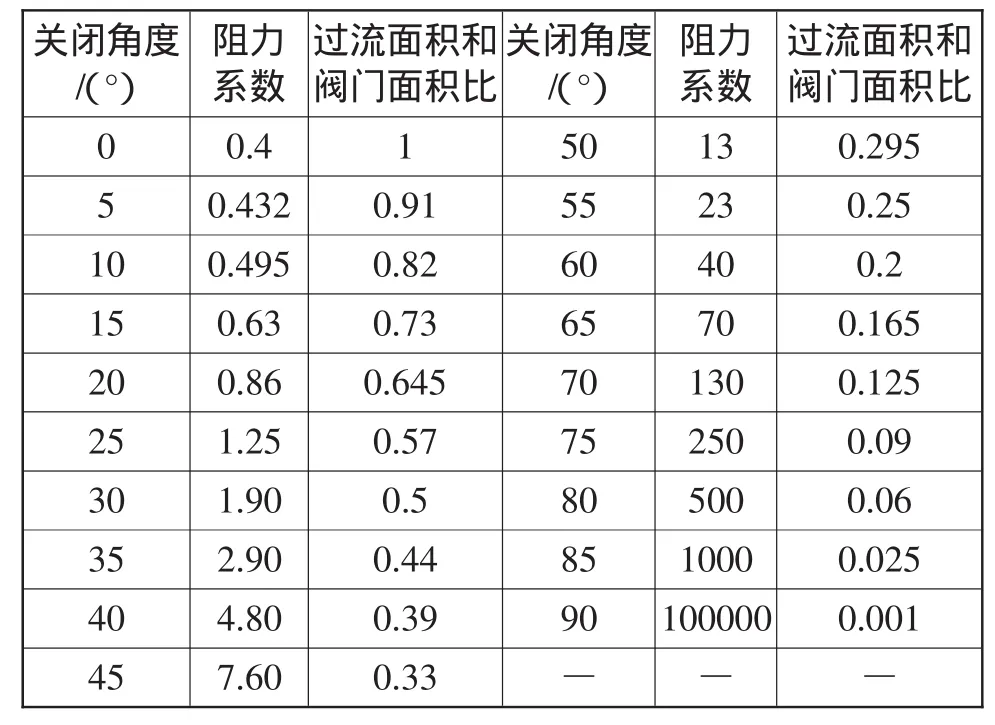
表1 阻力系数值及过流面积与阀门面积的比
在水力过渡过程的计算中,将关闭角度每隔5°的阻力系数和过流面积值输入计算机中,并求出相对应的水头损失系数。停泵后,任意时刻阀门关闭角对应的水头损失系数,用直线插入法计算。
在表1给出的数值及所采用的直线插入法的基础上,运用多元线性回归模型,给出过流面积与阀门面积的比值关于关闭角度的函数关系式,以及阻力系数和关闭角度的函数关系式,使水力过渡过程的数值模拟更为精确、易行。
2 多元线性回归模型
在实际问题中,影响结果y的因素往往不止一个。一般地,设有 x1,x2,…,xk,k 个因素,通常考虑如下的线性关系式[1]:
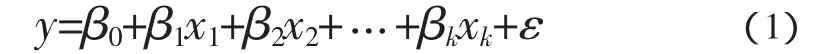
其中,β0,β1,…,βk为 k+1 个未知数,ε 是随机变量,一般假设 E(ε)=0,D(ε)=σ2,σ2>0。为了估计未知参数 β0,β1,…,βk及 σ2,对 y 与 x1,x2,…,xk同时作 n 次独立观察,得 n 组观察值(yt,xt1,xt2,…,xtk),t=1,2,…,n(n>k+1),满足关系式:
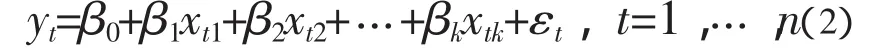
其中,ε1,…εn互不相关且均是与ε同分布的随机变量。为用矩阵形式表示上式,令:
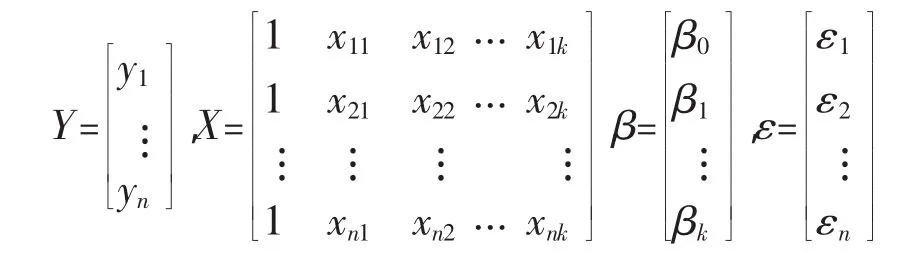
于是,多元线性回归模型可表示为:
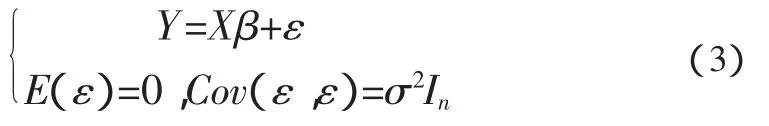
其中,In为n阶单位矩阵。
用最小二乘法,得β的最小二乘估计为:

3 数学模型的建立与求解
3.1 过流面积和阀门面积比值Y1与关闭角度x之间的函数关系
根据关闭角度x与过流面积和阀门面积比值Y1在表1中的数值,由MATLAB软件可绘制出(xi,Y1i)(其中i=1,2,…,19)的散点图,如图1所示。
根据图1,对过流面积和阀门面积比值Y1与关闭角度x的关系,可用二次函数进行回归分析。经回归分析的实验验证:①当只采用一个二次函数进行回归分析时,误差较大,所以采用分段函数的形式;②分段区间选择[0,50),[50,80),[80,85),[85,90]上较为精确;③在区间段[0,50),[50,80)适合用二次函数进行回归分析,这时误差很小,在区间[80,85],[85,90]上适合用原来的直线插入法,这样更符合实际。下面给出在区间[0,50),[50,80)上,用二次函数进行回归分析的计算方法。
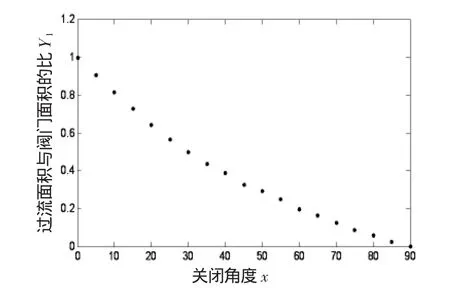
图1 (xi,Y1i)的散点图
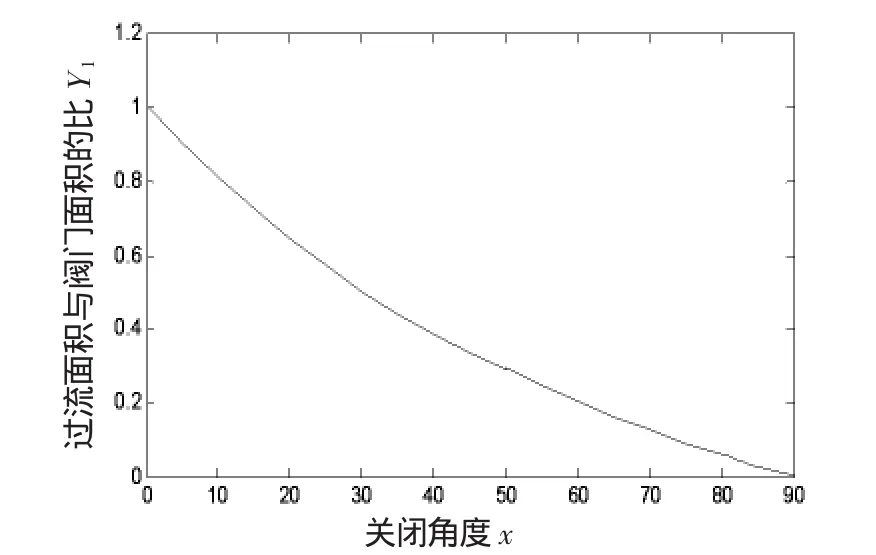
图2 Y1与x的函数关系图
在用二次函数y=β0+β1x+β2x2进行回归分析的计算时,首先令:xk=xk,(k=1,2),从而转换为多元线性回归模型,运用上述多元线性回归模型原理,并由MATLAB软件进行矩阵计算(MATLAB中矩阵计算方法见文献2),可以求得过流面积和阀门面积的比值 Y1与关闭角度 x 在区间[0,50),[50,80)上的函数关系为:
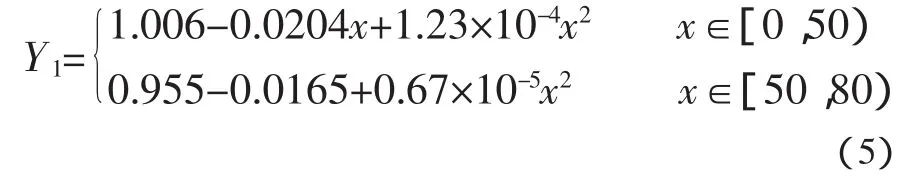
由MATLAB软件可绘制出(5)式以及在区间[80,85],[85,90]上运用直线插入法得到的函数图象,如图2。可以看出,图2与图1很接近。
为进一步判断由(5)式确定的函数关系的准确性,可以计算阀门关闭角度每隔5°时,由(5)式得到的过流面积和阀门面积的比值与原来的过流面积和阀门面积比值的相对误差,如表2。
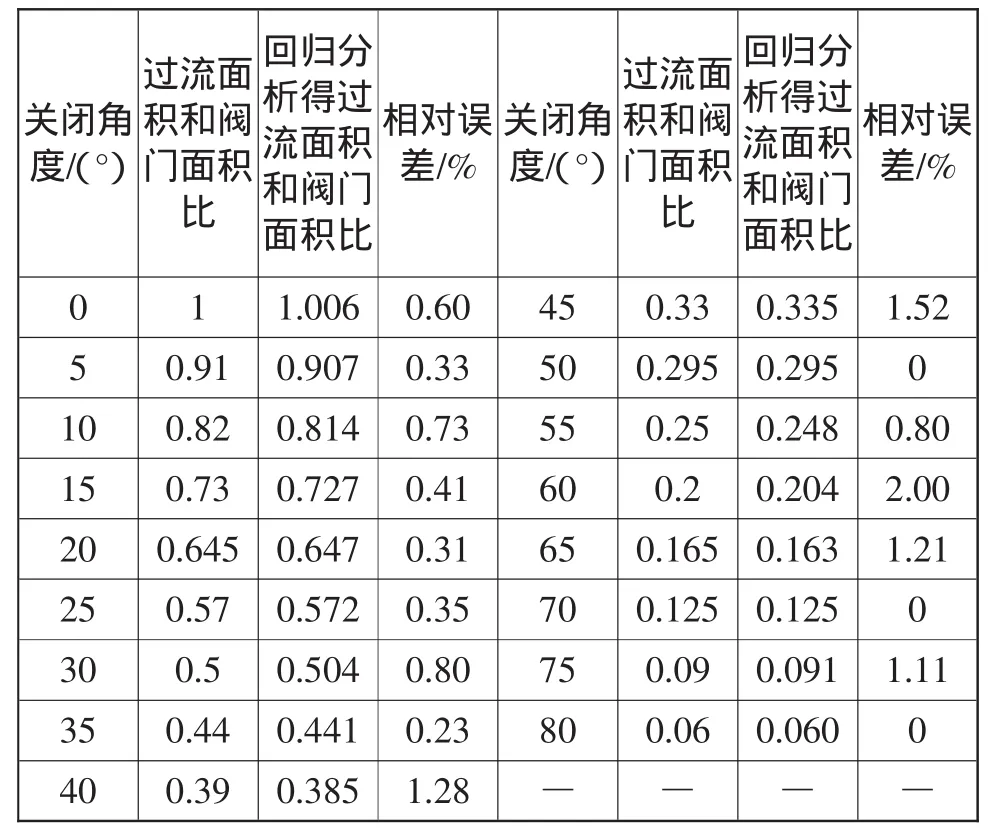
表2 过流面积和阀门面积比的相对误差
由表2可知,由(5)式得到的过流面积和阀门面积的比值与原来的过流面积和阀门面积比值的相对误差是很小的,即由多元线性回归模型得到的过流面积和阀门面积比值Y1与关闭角度 x在区间[0,50),[50,80)上的函数关系是合理的。
3.2 阻力系数Y2与关闭角度x的函数关系
根据表1中关闭角度x和相对应的阻力系数Y2的数值,可得到关闭角度x和对应的阻力系数的自然对数1nY2的数值,如表3。由MATLAB软件可绘制出(xi,1nY2i)(其中i=1,2,…,19)的散点图,如图 3 所示。
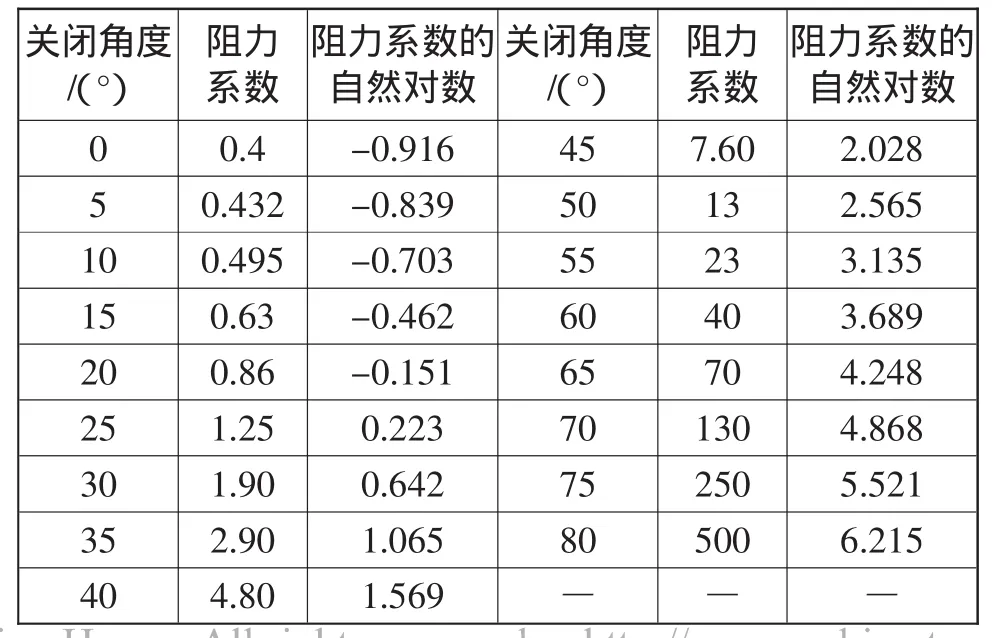
表3 关闭角度所对应阻力系数的自然对数
根据图3,对阻力系数的自然对数1nY2与关闭角度x的关系,可用二次函数进行回归分析。经回归分析的实验验证:①当只采用一个二次函数进行回归分析时,误差较大,所以需要采用分段函数的形式;②分段区间选择[0,25),[25,50),[50,80),[80,85],[85,90] 较为精确;③在区间段[0,25),[25,50),[50,80)用二次函数进行回归分析,这时误差很小,在区间[80,85],[85,90]上适合用原来的直线插入法。
对阻力系数的自然对数1nY2和关闭角度x,用二次函数1nY2=β0+β1x+β2x2进行回归分析,通过转换为多元线性回归模型,运用多元线性回归模型的原理,并由MATLAB软件进行矩阵计算,得:
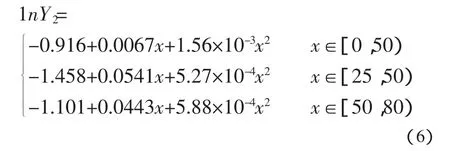
Y2可由(6)式推出。
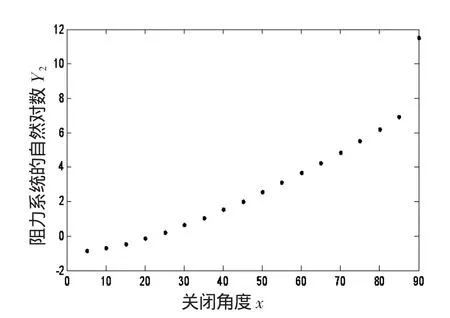
图3 (xi,1nY2i)的散点图
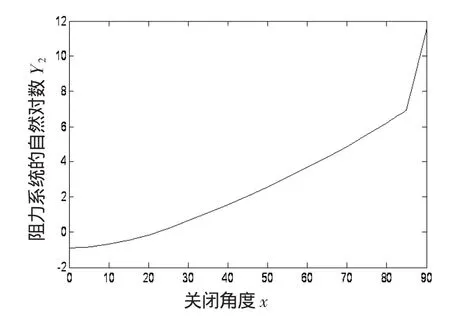
图4 Y2与x函数关系图
由MATLAB软件可绘制出(6)式及在区间[80,85],[85,90]上运用直线插入法得到的函数图象,如图4。可以看出,图4与图3较为接近。
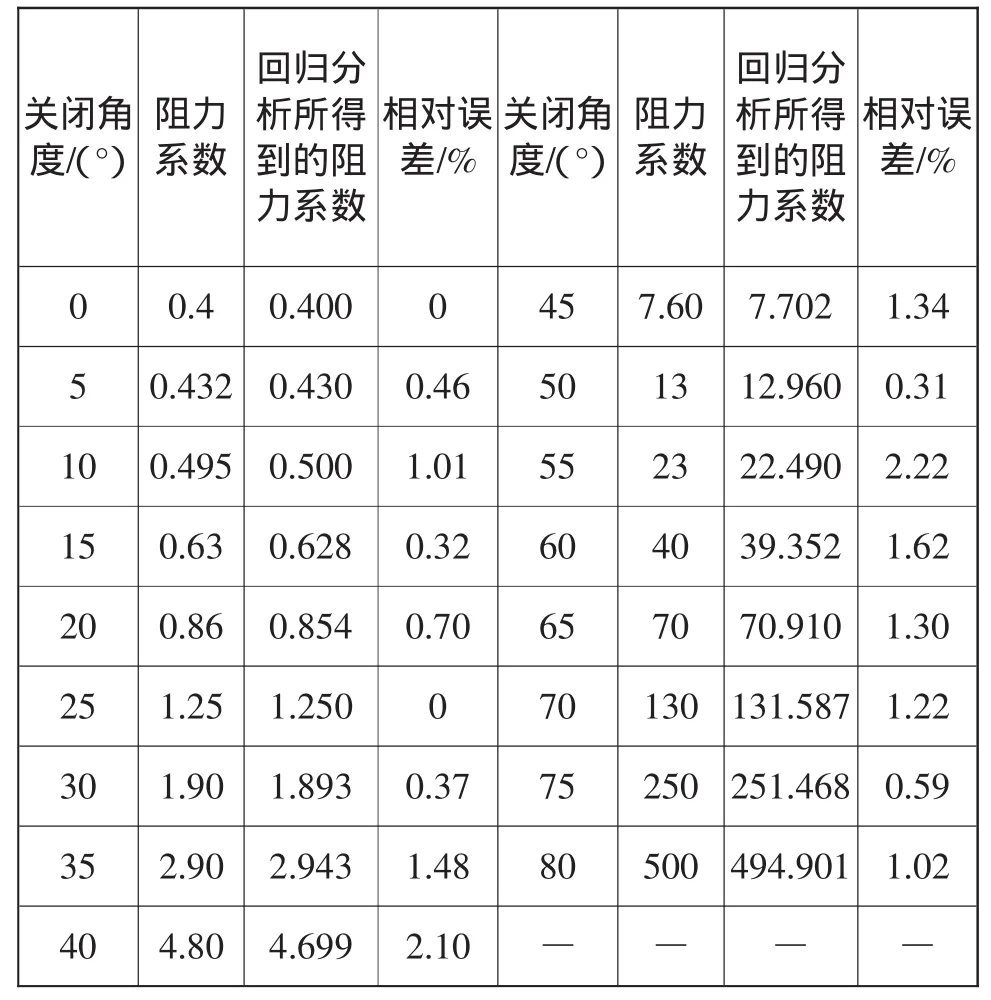
表4 阻力系数的相对误差
为进一步判断由(6)式所确定的阻力系数与关闭角度的函数关系的准确性,可以计算阀门关闭角度每隔5°时,由(6)式计算得到的阻力系数与原阻力系数的相对误差,如表4。
由表4可知,由(6)式所得阻力系数与原阻力系数的相对误差较小,所以,用多元线性回归模型得到的阻力系数Y2与关闭角度 x 在区间[0,25),[25,50),[50,80)上的函数关系是可行的。
4 结束语
根据蝶阀关闭角每隔5°时,相对应的阻力系数和过流面积与阀门面积比的离散数值,首先,用MATLAB软件分别绘制出过流面积与阀门面积的比值关于关闭角度的离散图,以及阻力系数和关闭角度的离散图;其次,运用多元线性回归分析原理,给出了在区间[0,80)上过流面积与阀门面积的比值关于关闭角度的函数关系式,以及阻力系数和关闭角度的函数关系式;最后,分别对两个函数关系式进行了相对误差分析,证实了两个函数关系的合理性和有效性。通过文中得到的两个函数关系式,可以使蝶阀关闭规律在水力过渡过程数值模拟的运用中变得更为精确、易行。
[1]孙荣恒.应用数理统计[M].北京:科学出版社,2003:195-198.
[2]龚剑,朱亮.MATLAB入门与提高[M].北京:清华大学出版社,2000:30-39.
